| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
bad_angel
Forumaš(ica)


Pridružen/a: 01. 11. 2008. (18:30:25)
Postovi: (43)16
Lokacija: svugdje po malo
|
 Postano: 14:15 sub, 13. 6. 2009 Naslov: zadaća 4 Postano: 14:15 sub, 13. 6. 2009 Naslov: zadaća 4 |
    |
|
|
Može mala pomoć oko zadatka 2.77?
Nađite površinu između krivulja y=2-x^2 i y^3=x^2.
Točke presjeka su -1 i 1, a ova prva krivulja je "gornja",pa treba izračunati integral (2-x^2-x^(2/3)) u granicama od -1 do 1,jel tako?
I meni primitivna funkcija tog ispada 2x - x^3/3 - 3x^(1/3), i onda mi rješenje kad izračunam s granicama ispadne -8/3..
a u rješenjima piše 32/15,i ja sam uvjerena da sam ja nešto krivo izračunala..
skužila sam.. krivo sam izderivirala x^(2/3).. sad je sve ok! :wink:
Može mala pomoć oko zadatka 2.77?
Nađite površinu između krivulja y=2-x^2 i y^3=x^2.
Točke presjeka su -1 i 1, a ova prva krivulja je "gornja",pa treba izračunati integral (2-x^2-x^(2/3)) u granicama od -1 do 1,jel tako?
I meni primitivna funkcija tog ispada 2x - x^3/3 - 3x^(1/3), i onda mi rješenje kad izračunam s granicama ispadne -8/3..
a u rješenjima piše 32/15,i ja sam uvjerena da sam ja nešto krivo izračunala..
skužila sam.. krivo sam izderivirala x^(2/3).. sad je sve ok! 
_________________
u raju je lijepo,ali u paklu je ekipa
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 14:36 sub, 13. 6. 2009 Naslov: Postano: 14:36 sub, 13. 6. 2009 Naslov: |
    |
|
|
krivo si integrirala x^2/3
integral od x^2/3 je (x^5/3)*(3/5)
krivo si integrirala x^2/3
integral od x^2/3 je (x^5/3)*(3/5)
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
bad_angel
Forumaš(ica)


Pridružen/a: 01. 11. 2008. (18:30:25)
Postovi: (43)16
Lokacija: svugdje po malo
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 18:19 sub, 13. 6. 2009 Naslov: Postano: 18:19 sub, 13. 6. 2009 Naslov: |
    |
|
|
[latex]\int{\frac{\cos{x}dx}{\sqrt{\sin{2x}}}}=\int{\left(\frac{1}{\sqrt{2}} \cdot \sqrt{\frac{\cos^2{x}}{\sin{x}\cos{x}}}\right)dx}=\frac{\sqrt{2}}{2}\int{\frac{dx}{\sqrt{\tan{x}}}}=(*)[/latex].
Sada uvodimo supstituciju, [latex]t=\sqrt{\tan{x}} \Longrightarrow x=\arctan{t^2} \Longrightarrow dx=\frac{2tdt}{1+t^4}[/latex], sada je jasno da je
[latex](*)=\sqrt{2}\int{\frac{dt}{t^4+1}}[/latex].
Vrijedi [latex]t^4+1=0 \Longleftrightarrow t \in \left\{\frac{\sqrt{2}}{2} \pm \frac{\sqrt{2}}{2}i,\, -\frac{\sqrt{2}}{2} \pm \frac{\sqrt{2}}{2}i\right\}[/latex], pa je
[latex]t^4+1=\left(t-\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i\right)\left(t-\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i\right)\left(t+\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i\right)\left(t+\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i\right)[/latex]
[latex]=\left(t^2-\sqrt{2}t+1\right)\left(t^2+\sqrt{2}t+1\right)[/latex].
Sada lako nalazimo da je
[latex]\frac{1}{t^4+1}=\frac{\frac{-\sqrt{2}}{4}t+\frac{1}{2}}{t^2-\sqrt{2}t+1}+\frac{\frac{\sqrt{2}}{4}t+\frac{1}{2}}{t^2+\sqrt{2}t+1}[/latex], konačno
[latex]\int{\frac{dt}{t^4+1}}=\frac{-\sqrt{2}}{8}\ln{\left(t^2-\sqrt{2}t+1\right)}+\frac{\sqrt{2}}{8}\ln{\left(t^2+\sqrt{2}t+1\right)}+[/latex]
[latex]+\frac{1}{4} \cdot \frac{\arctan{\frac{t-\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}}}}{\frac{\sqrt{2}}{2}}+\frac{1}{4} \cdot \frac{\arctan{\frac{t+\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}}}}{\frac{\sqrt{2}}{2}}+C=[/latex]
[latex]=\frac{\sqrt{2}}{8}\left(\ln{\frac{t^2+\sqrt{2}t+1}{t^2-\sqrt{2}t+1}}+2\arctan{\left(\sqrt{2}t-1\right)}+2\arctan{\left(\sqrt{2}t+1\right)}\right)+C[/latex].
Napokon,
[latex]\int{\frac{\cos{x}dx}{\sqrt{\sin{2x}}}}=[/latex]
[latex]=\frac{1}{4}\left\{\ln{\frac{\tan{x}+\sqrt{2\tan{x}}+1}{\tan{x}-\sqrt{2\tan{x}}+1}}+2\left[\arctan{\left(\sqrt{2\tan{x}}-1\right)}+\arctan{\left(\sqrt{2\tan{x}}+1\right)}\right]\right\}+C[/latex].
Iskreno se nadam da postoji ljepše ili barem jednostavnije rješenje :roll:
 . .
Sada uvodimo supstituciju, 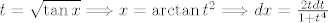 , sada je jasno da je , sada je jasno da je
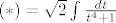 . .
Vrijedi 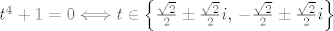 , pa je , pa je
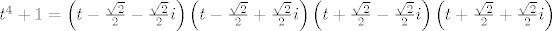
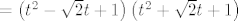 . .
Sada lako nalazimo da je
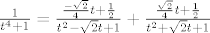 , konačno , konačno
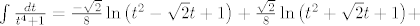
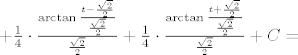
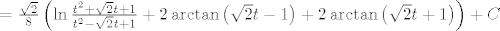 . .
Napokon,
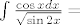
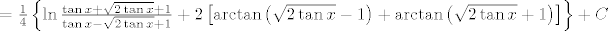 . .
Iskreno se nadam da postoji ljepše ili barem jednostavnije rješenje 
|
|
| [Vrh] |
|
bad_angel
Forumaš(ica)


Pridružen/a: 01. 11. 2008. (18:30:25)
Postovi: (43)16
Lokacija: svugdje po malo
|
|
| [Vrh] |
|
ambrozije
Forumaš(ica)
Pridružen/a: 29. 09. 2008. (19:18:04)
Postovi: (2C)16
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
bozidarsevo
Forumaš(ica)


Pridružen/a: 17. 09. 2008. (10:15:01)
Postovi: (1D1)16
Spol: 
Lokacija: Samobor
|
|
| [Vrh] |
|
ivek imudaš
Forumaš(ica)


Pridružen/a: 13. 11. 2007. (18:41:02)
Postovi: (67)16
Spol: 
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
ivek imudaš
Forumaš(ica)


Pridružen/a: 13. 11. 2007. (18:41:02)
Postovi: (67)16
Spol: 
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
ivek imudaš
Forumaš(ica)


Pridružen/a: 13. 11. 2007. (18:41:02)
Postovi: (67)16
Spol: 
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
ivek imudaš
Forumaš(ica)


Pridružen/a: 13. 11. 2007. (18:41:02)
Postovi: (67)16
Spol: 
|
 Postano: 15:27 sub, 27. 6. 2009 Naslov: Postano: 15:27 sub, 27. 6. 2009 Naslov: |
    |
|
|
[quote="Gino"]neznam dal je dobro ovo prvo... ostale nisam bas gledao...
nego:
[tt]sinx^1/2 < sinx <x[/tt]
zamjeni sa [tt]sinx^{1/2} < sinx <x[/tt]
pa ces dobit sta si htio
a sa [tt]\sqrt{\sin x}< \sin x <x[/tt] ces dobit jos ljepse :D :D[/quote]
da u pravu si, krivo je
[size=9][color=#999999]Added after 11 minutes:[/color][/size]
sorry cobs,zurio sam se nisam ni gledao sto pisem, u prvom mislim da mozes
sa granicnim kriterijem traziti limes sinx^(1/2)/x^(1/2) i dobiti da ti konvergira taj prvi valjda
kriva je bila usporedba sinx^(1/2)<sinx zato sto su brojevi iz <0,1>
| Gino (napisa): | neznam dal je dobro ovo prvo... ostale nisam bas gledao...
nego:
sinx^1/2 < sinx <x
zamjeni sa sinx^{1/2} < sinx <x
pa ces dobit sta si htio
a sa \sqrt{\sin x}< \sin x <x ces dobit jos ljepse   |
da u pravu si, krivo je
Added after 11 minutes:
sorry cobs,zurio sam se nisam ni gledao sto pisem, u prvom mislim da mozes
sa granicnim kriterijem traziti limes sinx^(1/2)/x^(1/2) i dobiti da ti konvergira taj prvi valjda
kriva je bila usporedba sinx^(1/2)<sinx zato sto su brojevi iz <0,1>
Zadnja promjena: ivek imudaš; 15:29 sub, 27. 6. 2009; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 15:28 sub, 27. 6. 2009 Naslov: Postano: 15:28 sub, 27. 6. 2009 Naslov: |
    |
|
|
hvala, imam jos par pitanja...
u zadatku 2.79 ispadne mi krivi rezultata, osim ak nije u skripti krivo napisano ( ja dobijem 3a^2*pi/8 a trebo bi dobit a^2*pi/4 )
u tom stavljam da su mi kutevi 0 i pi/2, i dobijem da mi je rjesenje a^2/8
i to pomnozim s tri zbog tri latice??? sam negdje pogrjesio?
u 2.85 stavim x = a*cos^3( t ), y = a*sin^3( t ) i opet kutevi su mi 0 i pi/2, ali opet dobivam neka kriva rjesenja.... ( jel ovo sto sam napravio dobro ili bi parametarska jednadzba trebala drukcije izgledat? )
u 2.88.... da nemam ovaj jadni winplot nikad ne bi ni skuzio kak to izgleda... pa s obzirom da imam crtez znam u biti sto treba uciniti, ali kako naci sjeciste ove dvije krivulje? ( winplot mi ih ne moze naci, a ako ih izjednacim dobijem da mi je x = pi/3, a kad pogledam grafove vidim da to nije u redu... pa kak dobit presjek, a i uostalom jel bi se to moglo rjesit bez da znas otprilike kako to izgleda? )
hvala, imam jos par pitanja...
u zadatku 2.79 ispadne mi krivi rezultata, osim ak nije u skripti krivo napisano ( ja dobijem 3a^2*pi/8 a trebo bi dobit a^2*pi/4 )
u tom stavljam da su mi kutevi 0 i pi/2, i dobijem da mi je rjesenje a^2/8
i to pomnozim s tri zbog tri latice??? sam negdje pogrjesio?
u 2.85 stavim x = a*cos^3( t ), y = a*sin^3( t ) i opet kutevi su mi 0 i pi/2, ali opet dobivam neka kriva rjesenja.... ( jel ovo sto sam napravio dobro ili bi parametarska jednadzba trebala drukcije izgledat? )
u 2.88.... da nemam ovaj jadni winplot nikad ne bi ni skuzio kak to izgleda... pa s obzirom da imam crtez znam u biti sto treba uciniti, ali kako naci sjeciste ove dvije krivulje? ( winplot mi ih ne moze naci, a ako ih izjednacim dobijem da mi je x = pi/3, a kad pogledam grafove vidim da to nije u redu... pa kak dobit presjek, a i uostalom jel bi se to moglo rjesit bez da znas otprilike kako to izgleda? )
|
|
| [Vrh] |
|
ivek imudaš
Forumaš(ica)


Pridružen/a: 13. 11. 2007. (18:41:02)
Postovi: (67)16
Spol: 
|
 Postano: 16:05 sub, 27. 6. 2009 Naslov: Postano: 16:05 sub, 27. 6. 2009 Naslov: |
    |
|
|
[quote="Cobs"]
u 2.85 stavim x = a*cos^3( t ), y = a*sin^3( t ) i opet kutevi su mi 0 i pi/2, ali opet dobivam neka kriva rjesenja.... ( jel ovo sto sam napravio dobro ili bi parametarska jednadzba trebala drukcije izgledat? )
[/quote]
pogledaj jedan moj post iznad, imas nest o tome
[size=9][color=#999999]Added after 9 minutes:[/color][/size]
[quote="Cobs"]
u 2.88.... da nemam ovaj jadni winplot nikad ne bi ni skuzio kak to izgleda... pa s obzirom da imam crtez znam u biti sto treba uciniti, ali kako naci sjeciste ove dvije krivulje? ( winplot mi ih ne moze naci, a ako ih izjednacim dobijem da mi je x = pi/3, a kad pogledam grafove vidim da to nije u redu... pa kak dobit presjek, a i uostalom jel bi se to moglo rjesit bez da znas otprilike kako to izgleda? )[/quote]
evo nacrtao sam otprilike kako to izgleda i ispa mi je neki polumjesec,
u stvari treba valjda naci povrsinu tog polumjeseca,
sjeciste nadjes tako da izjednacis po fi
i fi ti je iz [0,pi/2] pa ti je fi=pi/3
i sad izracunas 2puta povrsinu od 0 do pi/3 od kruznice u polarnim koordinatama i oduzmes od 2puta povsine kardioide u polarnim od 0 do pi/3
[size=9][color=#999999]Added after 23 minutes:[/color][/size]
[quote="Cobs"]hvala, imam jos par pitanja...
u zadatku 2.79 ispadne mi krivi rezultata, osim ak nije u skripti krivo napisano ( ja dobijem 3a^2*pi/8 a trebo bi dobit a^2*pi/4 )
u tom stavljam da su mi kutevi 0 i pi/2, i dobijem da mi je rjesenje a^2/8
i to pomnozim s tri zbog tri latice??? sam negdje pogrjesio?
[/quote]
greska ti je sto si ti pretpostavio da prvu od tri latice dobijes samo uvrstavanjem kuteva iz [0,pi/2]
npr za fi=pi+0.01 ti je asinf neki negativan broj pa ti je ta tocka na prvoj latici
a uostalom ne trebas traziti 3puta povrsinu od 0 do pi/2 nego nadji povrsinu od 0 do 2pi
meni je doduse u prvom racunanju ispalo a^2*pi/2 ali je vjerovatno neka greska u racunu
skuzio sam gdje mi je bila greska,treba racunati od 0 do pi jer je
[url]http://www07.wolframalpha.com/input/?i=polar+plot+sin3x+from+0+to+pi[/url]
imas nesto o tome i ovdje
[url]http://en.wikipedia.org/wiki/Rose_(mathematics)[/url]
| Cobs (napisa): |
u 2.85 stavim x = a*cos^3( t ), y = a*sin^3( t ) i opet kutevi su mi 0 i pi/2, ali opet dobivam neka kriva rjesenja.... ( jel ovo sto sam napravio dobro ili bi parametarska jednadzba trebala drukcije izgledat? )
|
pogledaj jedan moj post iznad, imas nest o tome
Added after 9 minutes:
| Cobs (napisa): |
u 2.88.... da nemam ovaj jadni winplot nikad ne bi ni skuzio kak to izgleda... pa s obzirom da imam crtez znam u biti sto treba uciniti, ali kako naci sjeciste ove dvije krivulje? ( winplot mi ih ne moze naci, a ako ih izjednacim dobijem da mi je x = pi/3, a kad pogledam grafove vidim da to nije u redu... pa kak dobit presjek, a i uostalom jel bi se to moglo rjesit bez da znas otprilike kako to izgleda? ) |
evo nacrtao sam otprilike kako to izgleda i ispa mi je neki polumjesec,
u stvari treba valjda naci povrsinu tog polumjeseca,
sjeciste nadjes tako da izjednacis po fi
i fi ti je iz [0,pi/2] pa ti je fi=pi/3
i sad izracunas 2puta povrsinu od 0 do pi/3 od kruznice u polarnim koordinatama i oduzmes od 2puta povsine kardioide u polarnim od 0 do pi/3
Added after 23 minutes:
| Cobs (napisa): | hvala, imam jos par pitanja...
u zadatku 2.79 ispadne mi krivi rezultata, osim ak nije u skripti krivo napisano ( ja dobijem 3a^2*pi/8 a trebo bi dobit a^2*pi/4 )
u tom stavljam da su mi kutevi 0 i pi/2, i dobijem da mi je rjesenje a^2/8
i to pomnozim s tri zbog tri latice??? sam negdje pogrjesio?
|
greska ti je sto si ti pretpostavio da prvu od tri latice dobijes samo uvrstavanjem kuteva iz [0,pi/2]
npr za fi=pi+0.01 ti je asinf neki negativan broj pa ti je ta tocka na prvoj latici
a uostalom ne trebas traziti 3puta povrsinu od 0 do pi/2 nego nadji povrsinu od 0 do 2pi
meni je doduse u prvom racunanju ispalo a^2*pi/2 ali je vjerovatno neka greska u racunu
skuzio sam gdje mi je bila greska,treba racunati od 0 do pi jer je
http://www07.wolframalpha.com/input/?i=polar+plot+sin3x+from+0+to+pi
imas nesto o tome i ovdje
http://en.wikipedia.org/wiki/Rose_(mathematics)
|
|
| [Vrh] |
|
|

















