| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
mycky1111
Forumaš(ica)

Pridružen/a: 26. 05. 2008. (11:59:07)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
mycky1111
Forumaš(ica)

Pridružen/a: 26. 05. 2008. (11:59:07)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
merien
Forumaš(ica)

Pridružen/a: 27. 08. 2008. (21:13:29)
Postovi: (15)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 10:00 pet, 15. 1. 2010 Naslov: Postano: 10:00 pet, 15. 1. 2010 Naslov: |
    |
|
|
Evo, nadam se da će sve biti OK, WolframAlpha je isto malo pomogao :
Nađimo prvo neodređeni integral od [latex]\displaystyle x^3e^{-\frac{ax^2}{2}}[/latex] po [latex]x[/latex]. Uzmimo supstituciju [latex]u:=x^2[/latex], pa je [latex]du=2xdx[/latex], tj. odgovarajući neodređeni integral je jednak [latex]\displaystyle \frac{1}{2}\int ue^{-\frac{au}{2}}du[/latex].
Sad ćemo parcijalno integrirati to, uzevši [latex]f=u[/latex] i [latex]\displaystyle dg=e^{-\frac{au}{2}}[/latex], tj [latex]\displaystyle g=-\frac{2e^{-\frac{au}{2}}}{a}[/latex]. Znamo da je [latex]\int fg'=fg-\int f'g[/latex], a obje stvari s desne strane nam je lako izračunati (tj. već smo ih izračunali, do na konstantu), pa imamo da je naš integral jednak [latex]\displaystyle \frac{1}{2}(-\frac{2ue^{-\frac{au}{2}}}{a}-\frac{4e^{-\frac{au}{2}}}{a^2})+c[/latex], gdje je [latex]c[/latex] neka konstanta. Sad možemo uvrstiti umjesto [latex]u[/latex] [latex]x^2[/latex], ali kako nama treba samo vrijednost, a ne sam neodređeni integral, dovoljno nam je saznati [latex]\displaystyle \lim_{u\to +\infty}\frac{1}{2}(-\frac{2ue^{-\frac{au}{2}}}{a}-\frac{4e^{-\frac{au}{2}}}{a^2})[/latex] i od toga oduzeti vrijednost za [latex]u=0[/latex].
Dalje vrijedi [latex]\displaystyle \lim_{u\to +\infty}\frac{1}{2}(-\frac{2ue^{-\frac{au}{2}}}{a}-\frac{4e^{-\frac{au}{2}}}{a^2})=\lim_{u\to +\infty}-\frac{ue^{-\frac{au}{2}}}{a}-\frac{2e^{-\frac{au}{2}}}{a^2}[/latex]. Lako vidimo da su oba pribrojnika u limesu [latex]0[/latex]: u drugom pribrojniku brojnik ide u [latex]0[/latex], a nazivnik je konstanta, a prvi pribrojnik je zapravo [latex]\displaystyle -\frac{u}{ae^{\frac{au}{2}}}[/latex], što očito ide u [latex]0[/latex] budući da gore imamo linearnu funkciju, a dolje eksponencijalnu (može i po L'Hospitalu, ako te veseli :)).
Dakle, traženi limes je [latex]0[/latex]. Budući da za [latex]u=0[/latex] dobivamo vrijednost [latex]\displaystyle -\frac{2}{a^2}[/latex], krajnje rješenje je [latex]\displaystyle 0-(-\frac{2}{a^2})=\frac{2}{a^2}[/latex].
Evo, nadam se da će sve biti OK, WolframAlpha je isto malo pomogao :
Nađimo prvo neodređeni integral od 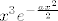 po po  . Uzmimo supstituciju . Uzmimo supstituciju 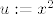 , pa je , pa je 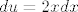 , tj. odgovarajući neodređeni integral je jednak , tj. odgovarajući neodređeni integral je jednak 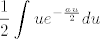 . .
Sad ćemo parcijalno integrirati to, uzevši 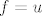 i i 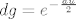 , tj , tj 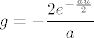 . Znamo da je . Znamo da je 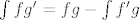 , a obje stvari s desne strane nam je lako izračunati (tj. već smo ih izračunali, do na konstantu), pa imamo da je naš integral jednak , a obje stvari s desne strane nam je lako izračunati (tj. već smo ih izračunali, do na konstantu), pa imamo da je naš integral jednak 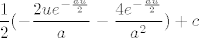 , gdje je , gdje je  neka konstanta. Sad možemo uvrstiti umjesto neka konstanta. Sad možemo uvrstiti umjesto  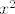 , ali kako nama treba samo vrijednost, a ne sam neodređeni integral, dovoljno nam je saznati , ali kako nama treba samo vrijednost, a ne sam neodređeni integral, dovoljno nam je saznati 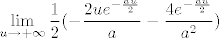 i od toga oduzeti vrijednost za i od toga oduzeti vrijednost za 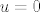 . .
Dalje vrijedi 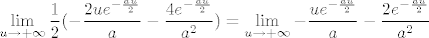 . Lako vidimo da su oba pribrojnika u limesu . Lako vidimo da su oba pribrojnika u limesu  : u drugom pribrojniku brojnik ide u : u drugom pribrojniku brojnik ide u  , a nazivnik je konstanta, a prvi pribrojnik je zapravo , a nazivnik je konstanta, a prvi pribrojnik je zapravo 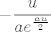 , što očito ide u , što očito ide u  budući da gore imamo linearnu funkciju, a dolje eksponencijalnu (može i po L'Hospitalu, ako te veseli budući da gore imamo linearnu funkciju, a dolje eksponencijalnu (može i po L'Hospitalu, ako te veseli  ). ).
Dakle, traženi limes je  . Budući da za . Budući da za 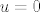 dobivamo vrijednost dobivamo vrijednost 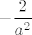 , krajnje rješenje je , krajnje rješenje je 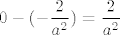 . .
|
|
| [Vrh] |
|
merien
Forumaš(ica)

Pridružen/a: 27. 08. 2008. (21:13:29)
Postovi: (15)16
|
|
| [Vrh] |
|
|









