| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
 Postano: 15:06 sub, 24. 10. 2009 Naslov: problem Postano: 15:06 sub, 24. 10. 2009 Naslov: problem |
    |
|
|
trebam pmoc...zapela sam...
{(1,1,0,0), (0,0,1,1), (1,0,1,0), (0,1,0,1), (1,0,0,1), (0,1,0,1)} , pokazati da je sustav izvodnica ua R4...hvala
trebam pmoc...zapela sam...
{(1,1,0,0), (0,0,1,1), (1,0,1,0), (0,1,0,1), (1,0,0,1), (0,1,0,1)} , pokazati da je sustav izvodnica ua R4...hvala
|
|
| [Vrh] |
|
ambrozije
Forumaš(ica)
Pridružen/a: 29. 09. 2008. (19:18:04)
Postovi: (2C)16
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
suza
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (14:37:50)
Postovi: (65)16
Spol: 
|
 Postano: 18:01 sub, 24. 10. 2009 Naslov: Postano: 18:01 sub, 24. 10. 2009 Naslov: |
    |
|
|
...da ne otvaram novu temu, a isto me muči jedan zadatk:
Kako pokazati da se vektor d=(gama)i+j+k može prikazati kao lin. kombinacija vektora a=i+pj+k, b=-i+j+k, c=-3i+j+pk ako su a,b,c komplanarni u V^3(O)? Za koji gama to vrijedi? :? [/img][/code][/quote]
...da ne otvaram novu temu, a isto me muči jedan zadatk:
Kako pokazati da se vektor d=(gama)i+j+k može prikazati kao lin. kombinacija vektora a=i+pj+k, b=-i+j+k, c=-3i+j+pk ako su a,b,c komplanarni u V^3(O)? Za koji gama to vrijedi?  [/img][/code][/quote] [/img][/code][/quote]
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
suza
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (14:37:50)
Postovi: (65)16
Spol: 
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
suza
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (14:37:50)
Postovi: (65)16
Spol: 
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
 Postano: 22:34 ned, 25. 10. 2009 Naslov: sustav izvodnica Postano: 22:34 ned, 25. 10. 2009 Naslov: sustav izvodnica |
    |
|
|
Pokazite da je
{(1, 1, 1, 1), (1, 1, 1, 0), (1, 1, 1, 2), (0, 1, 1, 1, ), (1, 0, 0, 0)}
sustav izvodnica za C4
pa ga reducirajte do neke baze prostora C4
Pokazite da je
{(1, 1, 1, 1), (1, 1, 1, 0), (1, 1, 1, 2), (0, 1, 1, 1, ), (1, 0, 0, 0)}
sustav izvodnica za C4
pa ga reducirajte do neke baze prostora C4
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
 Postano: 22:39 ned, 25. 10. 2009 Naslov: PItanjce Postano: 22:39 ned, 25. 10. 2009 Naslov: PItanjce |
    |
|
|
I ja imam 2 pitanja:
AKo recimo imam 2 polinoma, i sada ih trebam nadopuniti do baze za P5,recimo. Dali to izgleda ovako: 1,t,t^2,t^3,t^4,t^5, ili bez ovog nul-polinoma pa je to od t...t^6? (ili niti jedno niti drugo :)
I još jedno pitanje ako imam zadan neki skup M i treba provjeriti jeli on potprostor od R^4,i ispadne da je.Kako onda provjeriti jeli taj isti skup potprostor i od C^4?
I da komentiram ovaj prvi post, mislim da u zadatku piše da trebamo prvo provjeriti jeli to s.i za R^4,a tek ga onda reducirati do baze..Šta to ne znači da trebamo prvo uzet proizvoljni vektor iz R^4,i prikazat ga pomoću zadanih vektora?
I ja imam 2 pitanja:
AKo recimo imam 2 polinoma, i sada ih trebam nadopuniti do baze za P5,recimo. Dali to izgleda ovako: 1,t,t^2,t^3,t^4,t^5, ili bez ovog nul-polinoma pa je to od t...t^6? (ili niti jedno niti drugo 
I još jedno pitanje ako imam zadan neki skup M i treba provjeriti jeli on potprostor od R^4,i ispadne da je.Kako onda provjeriti jeli taj isti skup potprostor i od C^4?
I da komentiram ovaj prvi post, mislim da u zadatku piše da trebamo prvo provjeriti jeli to s.i za R^4,a tek ga onda reducirati do baze..Šta to ne znači da trebamo prvo uzet proizvoljni vektor iz R^4,i prikazat ga pomoću zadanih vektora?
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 23:15 ned, 25. 10. 2009 Naslov: Re: PItanjce Postano: 23:15 ned, 25. 10. 2009 Naslov: Re: PItanjce |
    |
|
|
[quote="pajopatak"]I ja imam 2 pitanja:
AKo recimo imam 2 polinoma, i sada ih trebam nadopuniti do baze za P5,recimo. Dali to izgleda ovako: 1,t,t^2,t^3,t^4,t^5, ili bez ovog nul-polinoma pa je to od t...t^6? (ili niti jedno niti drugo :)[/quote]
:?
ono NIJE nul-polinom
ako se ne varam [latex]t^6 \notin P_5[/latex] ... ono prvo
[quote="pajopatak"]I još jedno pitanje ako imam zadan neki skup M i treba provjeriti jeli on potprostor od R^4,i ispadne da je.Kako onda provjeriti jeli taj isti skup potprostor i od C^4?[/quote]
isto kao sto si i provjerio za [latex]\mathbb{R}^4[/latex], al najcesce ako je nesto iz [latex]\mathbb{R}^4[/latex] onda je i iz [latex]\mathbb{C}^4[/latex]
[quote="pajopatak"]Šta to ne znači da trebamo prvo uzet proizvoljni vektor iz R^4,i prikazat ga pomoću zadanih vektora?[/quote]
pa mozes kako hoces, ono mi se cini najbrze, u svakom slucaju, mislim da na vjezbama to radite tako da uzmete prva dva ako su zavisni, jednog maknete i uzmete sljedeceg, ako su nezavisni uzmete sljedeceg bez da ijednog maknete, i gledate jesu li sada ti nezavisni i tako dalje...
ako dodete do onoliko nezavisnih vektora kolika je dimenzija prostora ste gotovi, i odmah iz algoritma znate koje maknut, zavisne, koje ste vec makli, i eventualno one za koje jos niste ni gledali jer ste vec nasli bazu
| pajopatak (napisa): | I ja imam 2 pitanja:
AKo recimo imam 2 polinoma, i sada ih trebam nadopuniti do baze za P5,recimo. Dali to izgleda ovako: 1,t,t^2,t^3,t^4,t^5, ili bez ovog nul-polinoma pa je to od t...t^6? (ili niti jedno niti drugo  |

ono NIJE nul-polinom
ako se ne varam 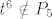 ... ono prvo ... ono prvo
| pajopatak (napisa): | | I još jedno pitanje ako imam zadan neki skup M i treba provjeriti jeli on potprostor od R^4,i ispadne da je.Kako onda provjeriti jeli taj isti skup potprostor i od C^4? |
isto kao sto si i provjerio za 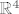 , al najcesce ako je nesto iz , al najcesce ako je nesto iz 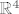 onda je i iz onda je i iz 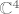
| pajopatak (napisa): | | Šta to ne znači da trebamo prvo uzet proizvoljni vektor iz R^4,i prikazat ga pomoću zadanih vektora? |
pa mozes kako hoces, ono mi se cini najbrze, u svakom slucaju, mislim da na vjezbama to radite tako da uzmete prva dva ako su zavisni, jednog maknete i uzmete sljedeceg, ako su nezavisni uzmete sljedeceg bez da ijednog maknete, i gledate jesu li sada ti nezavisni i tako dalje...
ako dodete do onoliko nezavisnih vektora kolika je dimenzija prostora ste gotovi, i odmah iz algoritma znate koje maknut, zavisne, koje ste vec makli, i eventualno one za koje jos niste ni gledali jer ste vec nasli bazu
_________________
Mario Berljafa
Zadnja promjena: Gino; 23:16 ned, 25. 10. 2009; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 23:16 ned, 25. 10. 2009 Naslov: Postano: 23:16 ned, 25. 10. 2009 Naslov: |
    |
|
|
@pajopatak:
ovo s polinomima - baza ti mora imat slobodni član. prostop P5 je prostor polinoma stupnja manjeg ili jednakog od pet (nekad je oznaka za stupnja manjeg ili jednakog od četiri, ovisno o sastavljaču zadatka :)) mora imat i slobodan član u bazi. taj slobodan član, isto ko i svi ovi ostali t-ovi, ne moraju baš biti 1, t,... može to bit i 7, 7t,... ovisi kako odabereš. svejedno je. ovo 1, t,... he samo kanonska baza, tebi je bitno da su oni nezavisni i da su najmanji skup izvodnica, ništ više od tog
@maty321:
ovak odokativno, odma vidiš da je prvi = četvrti plus peti pa ga odma makni
ostaje još provjerit da su nezavisni, to uzmi papir i olovku i raspiši, nema ti druge
@pajopatak:
ovo s polinomima - baza ti mora imat slobodni član. prostop P5 je prostor polinoma stupnja manjeg ili jednakog od pet (nekad je oznaka za stupnja manjeg ili jednakog od četiri, ovisno o sastavljaču zadatka  ) mora imat i slobodan član u bazi. taj slobodan član, isto ko i svi ovi ostali t-ovi, ne moraju baš biti 1, t,... može to bit i 7, 7t,... ovisi kako odabereš. svejedno je. ovo 1, t,... he samo kanonska baza, tebi je bitno da su oni nezavisni i da su najmanji skup izvodnica, ništ više od tog ) mora imat i slobodan član u bazi. taj slobodan član, isto ko i svi ovi ostali t-ovi, ne moraju baš biti 1, t,... može to bit i 7, 7t,... ovisi kako odabereš. svejedno je. ovo 1, t,... he samo kanonska baza, tebi je bitno da su oni nezavisni i da su najmanji skup izvodnica, ništ više od tog
@maty321:
ovak odokativno, odma vidiš da je prvi = četvrti plus peti pa ga odma makni
ostaje još provjerit da su nezavisni, to uzmi papir i olovku i raspiši, nema ti druge
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 0:45 pon, 26. 10. 2009 Naslov: Postano: 0:45 pon, 26. 10. 2009 Naslov: |
    |
|
|
[quote="pajopatak"]Hvala na brzim odgovorima,znači baza za R5, će imat 6 članova[/quote]
neće! baza za R5 če imati pet članova. to su "obični" vektori. jednako kao što je u R baza 1, R2 baza je (1,0), (0,1), u Rn će biti n takvih ili sličnih vektora
[quote](u to je uključen i taj [b]nezavisni[/b] član).[/quote]
svi članovi baze su nezavisni. u prostoru polinoma Pn postoji n članova tipa t^k 1<= k <= n i postoji slobodni član (mislim da se to tak zove), t^0 = 1. njih će ti bit n+1 komada. dakle, u prostoru P5 (što su polinomi stupnja manjeg ili jednakog od pet) biće ih šest komada: 1, t, t^2,..., t^5.
[quote]I sad ne kužim kako onda reducirati s.i do baze,jer kada je uključen taj nezavisni član,sve je polinome moguće prikazati pomoću njega?[/quote]
u tome i je fora. izgleda da si našo najmanji mogući sustav zvodnica.
sustav izvodnica je skup vektora koji nešto izvode :) to je skup preko kojeg se svaki drugi vektor iz promatranog prostora može prikazati kao linearna kombinacija vektora iz s.i. naza je najmanji sustav izvodnica. baza je najveći linearno nezavisan skup. vektorima iz baze je određen jedinstven prikaz nekog vektora iz prostora. sa s.i. to nije slučaj (barem ne generalno)
svaka baza sadrži onoliko vektora kolika je dimenzija prostora kojeg razapinje.
| pajopatak (napisa): | | Hvala na brzim odgovorima,znači baza za R5, će imat 6 članova |
neće! baza za R5 če imati pet članova. to su "obični" vektori. jednako kao što je u R baza 1, R2 baza je (1,0), (0,1), u Rn će biti n takvih ili sličnih vektora
| Citat: | | (u to je uključen i taj nezavisni član). |
svi članovi baze su nezavisni. u prostoru polinoma Pn postoji n članova tipa t^k 1⇐ k ⇐ n i postoji slobodni član (mislim da se to tak zove), t^0 = 1. njih će ti bit n+1 komada. dakle, u prostoru P5 (što su polinomi stupnja manjeg ili jednakog od pet) biće ih šest komada: 1, t, t^2,..., t^5.
| Citat: | | I sad ne kužim kako onda reducirati s.i do baze,jer kada je uključen taj nezavisni član,sve je polinome moguće prikazati pomoću njega? |
u tome i je fora. izgleda da si našo najmanji mogući sustav zvodnica.
sustav izvodnica je skup vektora koji nešto izvode  to je skup preko kojeg se svaki drugi vektor iz promatranog prostora može prikazati kao linearna kombinacija vektora iz s.i. naza je najmanji sustav izvodnica. baza je najveći linearno nezavisan skup. vektorima iz baze je određen jedinstven prikaz nekog vektora iz prostora. sa s.i. to nije slučaj (barem ne generalno) to je skup preko kojeg se svaki drugi vektor iz promatranog prostora može prikazati kao linearna kombinacija vektora iz s.i. naza je najmanji sustav izvodnica. baza je najveći linearno nezavisan skup. vektorima iz baze je određen jedinstven prikaz nekog vektora iz prostora. sa s.i. to nije slučaj (barem ne generalno)
svaka baza sadrži onoliko vektora kolika je dimenzija prostora kojeg razapinje.
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
homesweethome
Forumaš(ica)

Pridružen/a: 21. 10. 2009. (16:25:25)
Postovi: (1C)16
|
 Postano: 18:20 pon, 26. 10. 2009 Naslov: Re: problem Postano: 18:20 pon, 26. 10. 2009 Naslov: Re: problem |
    |
|
|
[quote="maty321"]trebam pmoc...zapela sam...
{(1,1,0,0), (0,0,1,1), (1,0,1,0), (0,1,0,1), (1,0,0,1), (0,1,0,1)} , pokazati da je sustav izvodnica ua R4...hvala[/quote]
da ali recimo nastavak zadatka glasi da nakon sto dokazemo da je sustav izvodnica, reduciramo ga do baze, onda bismo nekim drugim postupkom trebali dokazati da je skup s.izvodnica??
| maty321 (napisa): | trebam pmoc...zapela sam...
{(1,1,0,0), (0,0,1,1), (1,0,1,0), (0,1,0,1), (1,0,0,1), (0,1,0,1)} , pokazati da je sustav izvodnica ua R4...hvala |
da ali recimo nastavak zadatka glasi da nakon sto dokazemo da je sustav izvodnica, reduciramo ga do baze, onda bismo nekim drugim postupkom trebali dokazati da je skup s.izvodnica??
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 18:44 pon, 26. 10. 2009 Naslov: Postano: 18:44 pon, 26. 10. 2009 Naslov: |
    |
|
|
Skup izvodnica i baza nisu toliko različite stvari da bi postupak bio bitno različit.
Ovdje imaš 6 vektora, prostor je dimenzije 4, pa sigurno ima bar 2 viška. Makneš ta 2 (koja su linearna kombinacija nekih iz tog skupa), pa pogledaš dal još kojeg možeš maknut.
Ako ne - to je to, imaš lin nezavisan skup od 4 elementa u prostoru dimenzije 4, to je baza, pa je i skup izvodnica. I u taj skup možeš ubacivat kolko hoćeš, ostat će skup izvodnica (ako ubacuješ vektore iz R4 ) :D
Ako da - skup NIJE sistem izvodnica jer postoji vektor koji se ne može pomoću njih prikazat. (imaš vektora manje nego što je dimenzija). Tada niti polazni skup nije S.I.
Skup izvodnica i baza nisu toliko različite stvari da bi postupak bio bitno različit.
Ovdje imaš 6 vektora, prostor je dimenzije 4, pa sigurno ima bar 2 viška. Makneš ta 2 (koja su linearna kombinacija nekih iz tog skupa), pa pogledaš dal još kojeg možeš maknut.
Ako ne - to je to, imaš lin nezavisan skup od 4 elementa u prostoru dimenzije 4, to je baza, pa je i skup izvodnica. I u taj skup možeš ubacivat kolko hoćeš, ostat će skup izvodnica (ako ubacuješ vektore iz R4 ) 
Ako da - skup NIJE sistem izvodnica jer postoji vektor koji se ne može pomoću njih prikazat. (imaš vektora manje nego što je dimenzija). Tada niti polazni skup nije S.I.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 19:24 pon, 26. 10. 2009 Naslov: Postano: 19:24 pon, 26. 10. 2009 Naslov: |
    |
|
|
[quote="Luuka"]Ako da - skup NIJE sistem izvodnica jer postoji vektor koji se ne može pomoću njih prikazat. (imaš vektora manje nego što je dimenzija). Tada niti polazni skup nije S.I.[/quote]
ali ga možeš nadopuniti do baze dodavanjem vektora u taj skup, koji, naravno, mora biti linearno nezavisan o prethodnicima.
| Luuka (napisa): | | Ako da - skup NIJE sistem izvodnica jer postoji vektor koji se ne može pomoću njih prikazat. (imaš vektora manje nego što je dimenzija). Tada niti polazni skup nije S.I. |
ali ga možeš nadopuniti do baze dodavanjem vektora u taj skup, koji, naravno, mora biti linearno nezavisan o prethodnicima.
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
 Postano: 20:45 uto, 27. 10. 2009 Naslov: Postano: 20:45 uto, 27. 10. 2009 Naslov: |
    |
|
|
U R3
su zadani vektori a = (1, 2,−1), b = (1, 1, 1), c = (1, 3, λ), pri
cemu je λ ∈ R. Odrredite sve vrijednosti parametra λ za koje je skup
{a, b, c} baza prostora R3
. Za sve takve λ prikazite vektor v = (1, 1, 2)
kao linearnu kombinaciju vektora a, b, c.
Zanima me samo ovaj drugi dio....za sve takve....
hvala
U R3
su zadani vektori a = (1, 2,−1), b = (1, 1, 1), c = (1, 3, λ), pri
cemu je λ ∈ R. Odrredite sve vrijednosti parametra λ za koje je skup
{a, b, c} baza prostora R3
. Za sve takve λ prikazite vektor v = (1, 1, 2)
kao linearnu kombinaciju vektora a, b, c.
Zanima me samo ovaj drugi dio....za sve takve....
hvala
|
|
| [Vrh] |
|
|











