| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
marty
Forumaš(ica)
Pridružen/a: 26. 10. 2009. (17:40:41)
Postovi: (3D)16
Spol: 
|
 Postano: 18:12 pon, 26. 10. 2009 Naslov: Baze vektorskih prostora Postano: 18:12 pon, 26. 10. 2009 Naslov: Baze vektorskih prostora |
    |
|
|
molila bih da li moze tko napisati rješenja ovih zadataka... znam da su neki rjeseni na demonstraturama, ali za one koji nisu bili....
4.Neka je skup[latex] \{b_{1}, b_{2}, \ldots b_{n}\} [/latex]baza vektorskog prostora V te neka je a= [latex]\sum_{i=1}^{n}\alpha_{i}b_{i}\in \mathbb{V}[/latex] .pokažite da je skup [latex]\{a,b_{2}, , \ldots b_{n}\}[/latex] baza za V ako i samo ako je [latex]\alpha_{1}[/latex] različito od 0.
5.Neka je skup[latex] \{b_{1}, b_{2}, \ldots b_{n}\} [/latex] baza vektorskog prostora [latex]\mathbb{R}^{n}[/latex] .Dokaži da je on baza i za [latex]\mathbb{C}^{n}[/latex].
unaprijed hvala
molila bih da li moze tko napisati rješenja ovih zadataka... znam da su neki rjeseni na demonstraturama, ali za one koji nisu bili....
4.Neka je skup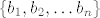 baza vektorskog prostora V te neka je a= baza vektorskog prostora V te neka je a= 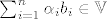 .pokažite da je skup .pokažite da je skup 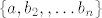 baza za V ako i samo ako je baza za V ako i samo ako je 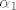 različito od 0. različito od 0.
5.Neka je skup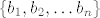 baza vektorskog prostora baza vektorskog prostora 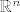 .Dokaži da je on baza i za .Dokaži da je on baza i za 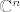 . .
unaprijed hvala
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 19:08 pon, 26. 10. 2009 Naslov: Postano: 19:08 pon, 26. 10. 2009 Naslov: |
    |
|
|
Oba su dosta lagana. :D
1.
->:
pretp suprotno, { a, b2, b3, ..., bn} baza i alfa1=0.
Tada je
[latex]a = \alpha_2 b_2 + ... + \alpha_n b_n[/latex]
pa je skup { a, b2, b3, ..., bn} očito linearno zavisan, pa ne može biti baza. Kontradikcija.
<-
opet pretp suprotno:
neka je alfa1!=0 i { a, b2, b3, ..., bn} nije baza
Pošto nije baza, tada je taj skup linearno zavisan. To znači da se neki vektor (npr a) može prikazati pomoću ostalih, tj da postoje skalari beta_i takvi da a ima prikaz:
[latex] a = \beta_2 b_2 +... + \beta_n b_n[/latex]
no, a je dan jedinstvenim prikazom u bazi [latex] a = \alpha_1 b_1 + \alpha_2 b_2 +... + \alpha_n b_n[/latex]. slijedi da je beta_i = alfa_i za i=2...n, i alfa1=0. Kontradikcija.
2.
jer je { b_1, ... b_n } baza za Rn, znači da se nul-vektor može samo na trivijalan način prikazat kao njihova linearna kombinacija (za skalare iz R).
Sad uzmemo skalare iz C ( alfa_k + i beta_k), i probamo nulu (0+0i) napisat pomoću njih. To ponovno vodi na trivijalan slučaj jer izjednačavanjem realnog i imaginarnog dijela na obje strane dobijemo isto - a to je prikaz nule pomoću realnih skalara.
p.s. drugi zadatak vrijedi samo za C^n nad poljem C. Kad imamo nad poljem R, onda baze nisu iste.
npr vektor (i,0) se ne može prikazat pomoću (0,1) i (1,0) upotrebom realnih skalara.
p.s. Ako netko ima precizniji dokaz drugog zadatka nek ga da, ovaj moj mi je sumnjiv... najteže je dokazat trivijalne stvari. :D
Oba su dosta lagana. 
1.
→:
pretp suprotno, { a, b2, b3, ..., bn} baza i alfa1=0.
Tada je

pa je skup { a, b2, b3, ..., bn} očito linearno zavisan, pa ne može biti baza. Kontradikcija.
←
opet pretp suprotno:
neka je alfa1!=0 i { a, b2, b3, ..., bn} nije baza
Pošto nije baza, tada je taj skup linearno zavisan. To znači da se neki vektor (npr a) može prikazati pomoću ostalih, tj da postoje skalari beta_i takvi da a ima prikaz:

no, a je dan jedinstvenim prikazom u bazi 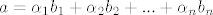 . slijedi da je beta_i = alfa_i za i=2...n, i alfa1=0. Kontradikcija. . slijedi da je beta_i = alfa_i za i=2...n, i alfa1=0. Kontradikcija.
2.
jer je { b_1, ... b_n } baza za Rn, znači da se nul-vektor može samo na trivijalan način prikazat kao njihova linearna kombinacija (za skalare iz R).
Sad uzmemo skalare iz C ( alfa_k + i beta_k), i probamo nulu (0+0i) napisat pomoću njih. To ponovno vodi na trivijalan slučaj jer izjednačavanjem realnog i imaginarnog dijela na obje strane dobijemo isto - a to je prikaz nule pomoću realnih skalara.
p.s. drugi zadatak vrijedi samo za C^n nad poljem C. Kad imamo nad poljem R, onda baze nisu iste.
npr vektor (i,0) se ne može prikazat pomoću (0,1) i (1,0) upotrebom realnih skalara.
p.s. Ako netko ima precizniji dokaz drugog zadatka nek ga da, ovaj moj mi je sumnjiv... najteže je dokazat trivijalne stvari. 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
marty
Forumaš(ica)
Pridružen/a: 26. 10. 2009. (17:40:41)
Postovi: (3D)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
 Postano: 21:26 sri, 28. 10. 2009 Naslov: Re: Baze vektorskih prostora Postano: 21:26 sri, 28. 10. 2009 Naslov: Re: Baze vektorskih prostora |
    |
|
|
[quote="marty"]
4.Neka je skup[latex] \{b_{1}, b_{2}, \ldots b_{n}\} [/latex]baza vektorskog prostora V te neka je a= [latex]\sum_{i=1}^{n}\alpha_{i}b_{i}\in \mathbb{V}[/latex] .pokažite da je skup [latex]\{a,b_{2}, , \ldots b_{n}\}[/latex] baza za V ako i samo ako je [latex]\alpha_{1}[/latex] različito od 0.
[/quote]
Kako to da ako je a= [latex]\sum_{i=1}^{n}\alpha_{i}b_{i}\in \mathbb{V}[/latex], a moze bit linearno nezavisan sa b_{i} i onda s njima ciniti bazu, ?!?! buni me to da je kombinacija b-ova a onda kasnije s njima nezavisan?!?!
| marty (napisa): |
4.Neka je skup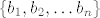 baza vektorskog prostora V te neka je a= baza vektorskog prostora V te neka je a= 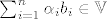 .pokažite da je skup .pokažite da je skup 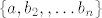 baza za V ako i samo ako je baza za V ako i samo ako je 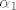 različito od 0. različito od 0.
|
Kako to da ako je a= 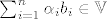 , a moze bit linearno nezavisan sa b_{i} i onda s njima ciniti bazu, ?!?! buni me to da je kombinacija b-ova a onda kasnije s njima nezavisan?!?! , a moze bit linearno nezavisan sa b_{i} i onda s njima ciniti bazu, ?!?! buni me to da je kombinacija b-ova a onda kasnije s njima nezavisan?!?!
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 21:46 sri, 28. 10. 2009 Naslov: Postano: 21:46 sri, 28. 10. 2009 Naslov: |
    |
|
|
stvar je upravo u onom alfa1!=0. Jer ako je ==0, onda je a lin komb b2,b3,...,bn pa {a,b1,...,bn} nikako ne može bit baza. No, ako ima u sebi i dio od b1, onda će biti lin nazavisan s ostalim bi-jevima, i sa njima će moć činit bazu.
stvar je upravo u onom alfa1!=0. Jer ako je ==0, onda je a lin komb b2,b3,...,bn pa {a,b1,...,bn} nikako ne može bit baza. No, ako ima u sebi i dio od b1, onda će biti lin nazavisan s ostalim bi-jevima, i sa njima će moć činit bazu.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
|
| [Vrh] |
|
|











