| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 19:20 pet, 30. 10. 2009 Naslov: Postano: 19:20 pet, 30. 10. 2009 Naslov: |
    |
|
|
Pretpostavljam da funkcija izgleda ovako: [latex]\ln^4(x)-3\ln^2(x)+2[/latex]. Budući da je [latex]\ln^n(x)[/latex] samo oznaka za [latex](\ln(x))^n[/latex], imamo [latex](\ln x)^4-3(\ln x)^2+2[/latex]. Sad vjerojatno otprilike shvaćaš kako bi kompozicija trebala izgledati: [latex]f_1(x)=\ln x[/latex], [latex]f_2(x)=x^4-3x^2+2[/latex]. Tada je [latex]f=f_2\circ f_1[/latex].
(Ako hoćeš, možeš još [latex]f_2[/latex] podijeliti na kompoziciju [latex]x^2-3x+2[/latex] i [latex]x^2[/latex], možda ti to nekako pomogne u rješavanju :).)
Pretpostavljam da funkcija izgleda ovako: 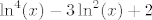 . Budući da je . Budući da je 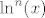 samo oznaka za samo oznaka za 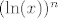 , imamo , imamo 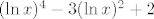 . Sad vjerojatno otprilike shvaćaš kako bi kompozicija trebala izgledati: . Sad vjerojatno otprilike shvaćaš kako bi kompozicija trebala izgledati: 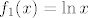 , , 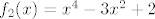 . Tada je . Tada je 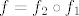 . .
(Ako hoćeš, možeš još 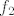 podijeliti na kompoziciju podijeliti na kompoziciju 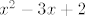 i i 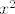 , možda ti to nekako pomogne u rješavanju , možda ti to nekako pomogne u rješavanju  .) .)
Zadnja promjena: mornik; 19:39 pet, 30. 10. 2009; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 20:27 pet, 30. 10. 2009 Naslov: Postano: 20:27 pet, 30. 10. 2009 Naslov: |
    |
|
|
Možda bi bilo korisno da sama napišeš dokle si došla, to je u najmanju ruku bolja vježba nego da samo pročitaš rješenje :). Stoga ću ja sad napisati generalnu ideju, neke međurezultate i finalni rezultat, a račun ostavljam tebi :P. Ozbiljno, nije teško... pri kraju postane malo dugačko i dosadno, ali ne i teško. Slobodno javi ako bude kakvih problema, OK? :)
Dakle, uzet ćemo (primijeti, oznake se ponešto razlikuju od onih koje sam koristio u prethodnom postu) [latex]f_3(x)=\ln x[/latex], [latex]f_2(x)=x^2[/latex] i [latex]f_1(x)=x^2-3x+2[/latex]. Sad je [latex]f=f_1\circ f_2\circ f_3[/latex].
Znamo iz formule koju konstantno spominjemo da vrijedi [latex]f^{-1}(A)=f_3^{-1}(f_2^{-1}({f_1^{-1}(A)))[/latex]. Sad uzmi [latex]A=[-1,0][/latex]. Nakon toga prvo odredi [latex]B=f_1^{-1}(A)[/latex]. To možeš "s grafa" (trebat će ti i malo računa, ali neznatno). Nakon toga odredi [latex]C=f_2^{-1}(B)=f_2^{-1}(f_1^{-1}(A))[/latex], ponovno istim postupkom. Na kraju, odredi [latex]f_3^{-1}(C)=f_3^{-1}(f_2^{-1}(f_1^{-1}(A)))[/latex]. To je tvoje finalno rješenje.
Ako se ne varam, [latex]B=[1,2][/latex] (možemo usput primijetiti da je [latex]f_1>-1[/latex], to nam olakšava traženje [latex]B[/latex]). Nadalje, [latex]C=[-\sqrt{2},-1]\cup[1,\sqrt{2}][/latex], a finalno rješenje bi trebalo biti [latex][e^{-\sqrt{2}},e^{-1}]\cup [e,e^{\sqrt{2}}][/latex]. Evo, i WolframAlpha se slaže :).
Možda bi bilo korisno da sama napišeš dokle si došla, to je u najmanju ruku bolja vježba nego da samo pročitaš rješenje  . Stoga ću ja sad napisati generalnu ideju, neke međurezultate i finalni rezultat, a račun ostavljam tebi . Stoga ću ja sad napisati generalnu ideju, neke međurezultate i finalni rezultat, a račun ostavljam tebi  . Ozbiljno, nije teško... pri kraju postane malo dugačko i dosadno, ali ne i teško. Slobodno javi ako bude kakvih problema, OK? . Ozbiljno, nije teško... pri kraju postane malo dugačko i dosadno, ali ne i teško. Slobodno javi ako bude kakvih problema, OK? 
Dakle, uzet ćemo (primijeti, oznake se ponešto razlikuju od onih koje sam koristio u prethodnom postu) 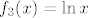 , , 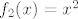 i i 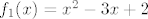 . Sad je . Sad je 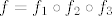 . .
Znamo iz formule koju konstantno spominjemo da vrijedi 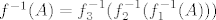 . Sad uzmi . Sad uzmi 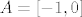 . Nakon toga prvo odredi . Nakon toga prvo odredi 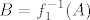 . To možeš "s grafa" (trebat će ti i malo računa, ali neznatno). Nakon toga odredi . To možeš "s grafa" (trebat će ti i malo računa, ali neznatno). Nakon toga odredi 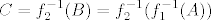 , ponovno istim postupkom. Na kraju, odredi , ponovno istim postupkom. Na kraju, odredi 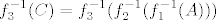 . To je tvoje finalno rješenje. . To je tvoje finalno rješenje.
Ako se ne varam, 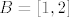 (možemo usput primijetiti da je (možemo usput primijetiti da je 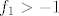 , to nam olakšava traženje , to nam olakšava traženje  ). Nadalje, ). Nadalje, 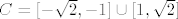 , a finalno rješenje bi trebalo biti , a finalno rješenje bi trebalo biti 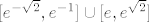 . Evo, i WolframAlpha se slaže . Evo, i WolframAlpha se slaže  . .
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
Darija.x
Forumaš(ica)
Pridružen/a: 10. 07. 2008. (18:31:47)
Postovi: (34)16
Lokacija: Velika Gorica
|
|
| [Vrh] |
|
marty
Forumaš(ica)
Pridružen/a: 26. 10. 2009. (17:40:41)
Postovi: (3D)16
Spol: 
|
|
| [Vrh] |
|
Jay-Mo
Forumaš(ica)

Pridružen/a: 14. 10. 2009. (15:58:25)
Postovi: (C)16
Spol: 
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 3:04 ned, 1. 11. 2009 Naslov: Postano: 3:04 ned, 1. 11. 2009 Naslov: |
    |
|
|
@Darija.x: [url=http://degiorgi.math.hr/forum/viewtopic.php?p=124718#124718]klik[/url] :)
@marty: rastaviš na što je elementarnije moguće funkcije (da ti bude lakše), npr. u tom zadatku bi se moglo:
[latex]f_1(x) = \log_2(x)[/latex], (definiramo samo za pozitivne realne brojeve!)
[latex]f_2(x) = 2x + 2[/latex],
[latex]f_3(x) = \sin{x}[/latex],
[latex]f_4(x) = \frac{\pi}{6}x[/latex].
Sada je [latex]f(x) = \left(f_1 \circ f_2 \circ f_3 \circ f_4\right)(x)[/latex].
Dalje računamo:
[latex]f_4\left(\left\langle-3,\, 4\right\rangle\right) = \left\langle\frac{-\pi}{2},\, \frac{2 \pi}{3}\right\rangle[/latex],
[latex]f_3\left(\left\langle\frac{-\pi}{2},\, \frac{2 \pi}{3}\right\rangle\right) = \left\langle-1,\, 1\right][/latex], (funkcija sinus poprimi sve moguće vrijednosti na [latex]\left[\frac{-\pi}{2},\, \frac{\pi}{2}\right][/latex])
[latex]f_2\left(\left\langle-1,\, 1\right]\right) = \left\langle0,\, 4\right][/latex],
[latex]f_1\left(\left\langle0,\, 4\right]\right) = \left\langle-\infty,\, 2\right][/latex]. (lako zaključujemo iz grafa logaritamske funkcije)
Dakle, [latex]f\left(\left\langle-3,\, 4\right\rangle\right) = \left\langle-\infty,\, 2\right][/latex].
@Darija.x: klik 
@marty: rastaviš na što je elementarnije moguće funkcije (da ti bude lakše), npr. u tom zadatku bi se moglo:
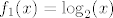 , (definiramo samo za pozitivne realne brojeve!) , (definiramo samo za pozitivne realne brojeve!)
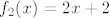 , ,
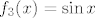 , ,
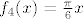 . .
Sada je 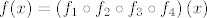 . .
Dalje računamo:
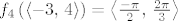 , ,
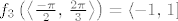 , (funkcija sinus poprimi sve moguće vrijednosti na , (funkcija sinus poprimi sve moguće vrijednosti na 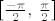 ) )
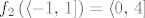 , ,
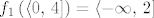 . (lako zaključujemo iz grafa logaritamske funkcije) . (lako zaključujemo iz grafa logaritamske funkcije)
Dakle, 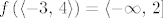 . .
|
|
| [Vrh] |
|
marty
Forumaš(ica)
Pridružen/a: 26. 10. 2009. (17:40:41)
Postovi: (3D)16
Spol: 
|
|
| [Vrh] |
|
Darija.x
Forumaš(ica)
Pridružen/a: 10. 07. 2008. (18:31:47)
Postovi: (34)16
Lokacija: Velika Gorica
|
|
| [Vrh] |
|
|








