| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
bimar
Forumaš(ica)


Pridružen/a: 16. 11. 2008. (14:45:25)
Postovi: (61)16
Lokacija: arkadija
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
bimar
Forumaš(ica)


Pridružen/a: 16. 11. 2008. (14:45:25)
Postovi: (61)16
Lokacija: arkadija
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
 Postano: 17:00 sub, 7. 11. 2009 Naslov: Postano: 17:00 sub, 7. 11. 2009 Naslov: |
    |
|
|
Znaci ti odaberes jednu boju koje nece bit u tvom izboru, a onda iz ostatka izaberes 13 karata. Recimo da je izabrana boja srce. Onda si tu ukljucio sve izbore kad nemas niti jedno srce, specijalno, slucaj kad imas svih trinaest pikova. Ako izaberes tref, opet su tu svi izbori kad nemas niti jednog trefa, ali opet je slucaj kad je izabrano trinaest pikova tu ubrojen. Isto i sa karom. Jedino kad izaberes da nemas pikova, tu konfiguraciju od 13 pikova ne ubrajas. Dakle triput si ubrojio konfiguraciju sa 13 pikova. Lako sad vidis da si konfiguracije koje sadrze samo dvije boje ubrojio dvaput. Jasnije?
Znaci ti odaberes jednu boju koje nece bit u tvom izboru, a onda iz ostatka izaberes 13 karata. Recimo da je izabrana boja srce. Onda si tu ukljucio sve izbore kad nemas niti jedno srce, specijalno, slucaj kad imas svih trinaest pikova. Ako izaberes tref, opet su tu svi izbori kad nemas niti jednog trefa, ali opet je slucaj kad je izabrano trinaest pikova tu ubrojen. Isto i sa karom. Jedino kad izaberes da nemas pikova, tu konfiguraciju od 13 pikova ne ubrajas. Dakle triput si ubrojio konfiguraciju sa 13 pikova. Lako sad vidis da si konfiguracije koje sadrze samo dvije boje ubrojio dvaput. Jasnije?
_________________
Jedan je smjer očit, a drugi je trivijalan.
|
|
| [Vrh] |
|
Mrs. Bean
Forumaš(ica)

Pridružen/a: 29. 06. 2009. (22:03:56)
Postovi: (31)16
Spol: 
|
|
| [Vrh] |
|
nameless
Forumaš(ica)


Pridružen/a: 29. 09. 2007. (13:59:36)
Postovi: (58)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
ivek imudaš
Forumaš(ica)


Pridružen/a: 13. 11. 2007. (18:41:02)
Postovi: (67)16
Spol: 
|
|
| [Vrh] |
|
bimar
Forumaš(ica)


Pridružen/a: 16. 11. 2008. (14:45:25)
Postovi: (61)16
Lokacija: arkadija
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
 Postano: 14:39 uto, 10. 11. 2009 Naslov: Postano: 14:39 uto, 10. 11. 2009 Naslov: |
    |
|
|
imam još 2 pitanja, za sada....
1. kako se računa [latex]\displaystyle\sum_{i=0}^{n}(\frac{5}{6})^i [/latex] ? zaboravih to :(
2. http://web.math.hr/nastava/uuv/files/chap1.pdf (zad.1.17.)
Koristimo prostor el.dog. pogodan za računanje Lukinog dobitka: [latex]omega=\{ (X_1, X_2, X_3,...,X_{3n+1}) : X_1, X_4, ..., X_{3n-2} \in\{1, 2, 3, 4, 5\}, X_{3n+1}=6 \}[/latex]
D={Luka je dobio 6 drugi po redu}, [latex]D_n[/latex]={Luka je dobio 6 drugi po redu u (3n+1)-vom bacanju}
[latex]D=\displaystyle\cup_{n=1}^{\infty}D_n[/latex]
sada slijedi dio koji mi nije jasan
[latex]P(D_n)=\frac{5^n\cdot(6^n-5^n)\cdot5^n+5^n\cdot5^n\cdot(6^n-5^n)}{6^{3n+1}}[/latex]
dakle, prvi sumand je kada Karlo prvi dobije 6, a drugi sumand kada M prvi dobije 6, ali ne razumijem, kako smo to dobili?
[size=9][color=#999999]Added after 1 minutes:[/color][/size]
[quote="Novi"]Jel se meni cini ili ti to racunas [latex]P(B)[/latex] da bi liniju ispod mirne duše uvrstila da je [latex]P(B)=\frac{3^n}{6^n}[/latex]?[/quote]
ups, tu je trebalo pisati [latex]P(B_1)[/latex]
imam još 2 pitanja, za sada....
1. kako se računa 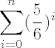 ? zaboravih to ? zaboravih to 
2. http://web.math.hr/nastava/uuv/files/chap1.pdf (zad.1.17.)
Koristimo prostor el.dog. pogodan za računanje Lukinog dobitka: 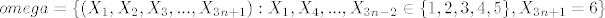
D={Luka je dobio 6 drugi po redu}, 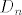 ={Luka je dobio 6 drugi po redu u (3n+1)-vom bacanju} ={Luka je dobio 6 drugi po redu u (3n+1)-vom bacanju}
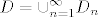
sada slijedi dio koji mi nije jasan
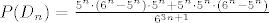
dakle, prvi sumand je kada Karlo prvi dobije 6, a drugi sumand kada M prvi dobije 6, ali ne razumijem, kako smo to dobili?
Added after 1 minutes:
| Novi (napisa): | Jel se meni cini ili ti to racunas 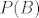 da bi liniju ispod mirne duše uvrstila da je da bi liniju ispod mirne duše uvrstila da je 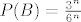 ? ? |
ups, tu je trebalo pisati 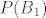
_________________
Granice mogućega možemo odrediti samo onda ako ih prijeđemo odlaskom u nemoguće
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
 Postano: 14:50 uto, 10. 11. 2009 Naslov: Postano: 14:50 uto, 10. 11. 2009 Naslov: |
    |
|
|
Da sad vidim. U svakom slucaju, tocno je ono s vjezbi. Ti kad racunas da je produkt paran zaboravljas da je dovoljno da imas jednu kocku s parnim brojem da bi citav produkt bio paran, tako da npr. [latex]P(B1)[/latex] nemoze bit [latex]\frac{3^n}{6^n}[/latex] vec [latex]1-\frac{3^n}{6^n}[/latex]. Dalje [latex]\displaystyle\sum_{i=0}^{n}x^i = \frac{1-x^{n+1}}{1-x}[/latex]. I jos ovo zadnje. Znaci ti imas niz duljine [latex]3n+1[/latex]. Na Lukine pozicije prije zadnje moras stavit sve osim sestica, a na poslijednju poziciju sest, jer je tad dobio prvu. To je na [latex]5^n \cdot 1[/latex] nacina. Za igraca koji nije dobio jos sesticu na svih njegovih [latex]n[/latex] mjesta stavljas sve osim petice na [latex]5^n[/latex] nacina. I naposlijetku igrac koji je dobio sesticu prije Luke na prethodnim pozicijama ima bilo sto sto ima bar jednu sesticu (koja je stoga prije ove Lukine). Uoci da on moze dobivat sve sestice redom, to je svejedno kad ju je jednom dobio. To se radi na [latex]6^n-5^n[/latex] nacina. Od svih mogucnosti oduzmemo one u kojima on nije dobio sesticu. I podijeli se sa svim mogucim ishodima za nizove duljine [latex]3n+1[/latex] sto je ono u nazivniku. Analogno kad je Marko prije Luke dobio sesticu, a Luka ju je dobio u n-tom krugu. Jasnije?
Da sad vidim. U svakom slucaju, tocno je ono s vjezbi. Ti kad racunas da je produkt paran zaboravljas da je dovoljno da imas jednu kocku s parnim brojem da bi citav produkt bio paran, tako da npr. 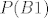 nemoze bit nemoze bit 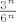 vec vec 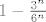 . Dalje . Dalje 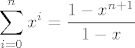 . I jos ovo zadnje. Znaci ti imas niz duljine . I jos ovo zadnje. Znaci ti imas niz duljine 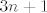 . Na Lukine pozicije prije zadnje moras stavit sve osim sestica, a na poslijednju poziciju sest, jer je tad dobio prvu. To je na . Na Lukine pozicije prije zadnje moras stavit sve osim sestica, a na poslijednju poziciju sest, jer je tad dobio prvu. To je na 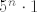 nacina. Za igraca koji nije dobio jos sesticu na svih njegovih nacina. Za igraca koji nije dobio jos sesticu na svih njegovih  mjesta stavljas sve osim petice na mjesta stavljas sve osim petice na 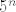 nacina. I naposlijetku igrac koji je dobio sesticu prije Luke na prethodnim pozicijama ima bilo sto sto ima bar jednu sesticu (koja je stoga prije ove Lukine). Uoci da on moze dobivat sve sestice redom, to je svejedno kad ju je jednom dobio. To se radi na nacina. I naposlijetku igrac koji je dobio sesticu prije Luke na prethodnim pozicijama ima bilo sto sto ima bar jednu sesticu (koja je stoga prije ove Lukine). Uoci da on moze dobivat sve sestice redom, to je svejedno kad ju je jednom dobio. To se radi na 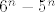 nacina. Od svih mogucnosti oduzmemo one u kojima on nije dobio sesticu. I podijeli se sa svim mogucim ishodima za nizove duljine nacina. Od svih mogucnosti oduzmemo one u kojima on nije dobio sesticu. I podijeli se sa svim mogucim ishodima za nizove duljine 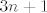 sto je ono u nazivniku. Analogno kad je Marko prije Luke dobio sesticu, a Luka ju je dobio u n-tom krugu. Jasnije? sto je ono u nazivniku. Analogno kad je Marko prije Luke dobio sesticu, a Luka ju je dobio u n-tom krugu. Jasnije?
_________________
Jedan je smjer očit, a drugi je trivijalan.
Zadnja promjena: Novi; 15:01 uto, 10. 11. 2009; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
ddduuu
Forumaš(ica)

Pridružen/a: 16. 11. 2008. (12:31:48)
Postovi: (109)16
|
 Postano: 15:27 uto, 10. 11. 2009 Naslov: Postano: 15:27 uto, 10. 11. 2009 Naslov: |
    |
|
|
Zadatak iz kolokvija 2007...
Dvije prijateljice planiraju zajednicko putovanje, ali se ne mogu sloziti oko destinacije:Ana bi na Kubu, a Iva radije u Argentinu. Odlucile su odluku prepustiti sreci pa su uzele 5 (simetricnih) kockica, a kako je Ani uskoro rodendan (25:11:), ona je zadala pravila: ako zbroj brojeva koji padnu bude jednak danu njezina rodenja ili padne bar
jednom njen omiljeni broj (5) ili produkt dobivenih brojeva bude djeljiv s 10, ici ce na Kubu. Kolika je vjerojatnost Anine trece opcije? Je li mudro odabrala (tj. kolika je vjerojatnost da ce izbor pasti na Kubu)?
Jel netko moze objasnit ovaj dio "ako zbroj brojeva koji padnu bude jednak danu njezina rodenja". Ovo je nesto iz kombinatorike, ali ne znan kako da izracunan broj kombinacija. Hvala:)
Zadatak iz kolokvija 2007...
Dvije prijateljice planiraju zajednicko putovanje, ali se ne mogu sloziti oko destinacije:Ana bi na Kubu, a Iva radije u Argentinu. Odlucile su odluku prepustiti sreci pa su uzele 5 (simetricnih) kockica, a kako je Ani uskoro rodendan (25:11:), ona je zadala pravila: ako zbroj brojeva koji padnu bude jednak danu njezina rodenja ili padne bar
jednom njen omiljeni broj (5) ili produkt dobivenih brojeva bude djeljiv s 10, ici ce na Kubu. Kolika je vjerojatnost Anine trece opcije? Je li mudro odabrala (tj. kolika je vjerojatnost da ce izbor pasti na Kubu)?
Jel netko moze objasnit ovaj dio "ako zbroj brojeva koji padnu bude jednak danu njezina rodenja". Ovo je nesto iz kombinatorike, ali ne znan kako da izracunan broj kombinacija. Hvala:)
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Mrs. Bean
Forumaš(ica)

Pridružen/a: 29. 06. 2009. (22:03:56)
Postovi: (31)16
Spol: 
|
 Postano: 17:24 uto, 10. 11. 2009 Naslov: Postano: 17:24 uto, 10. 11. 2009 Naslov: |
    |
|
|
[quote="ddduuu"]
Jel netko moze objasnit ovaj dio "ako zbroj brojeva koji padnu bude jednak danu njezina rodenja". Ovo je nesto iz kombinatorike, ali ne znan kako da izracunan broj kombinacija. Hvala:)[/quote]
ja sam ovo radila ovako:
A={(x1,x2,x3,x4,x5),xi e {1...6}, x1+x2+...+x5=25}
i sada sam radila kao na diskretnoj:
uvjet je 1<=xi<=6 pa je onda
yi=xi-1, dobije se
y1+y2+...+y5=20 i sad jos imam uvjet
yi<=6, kale zi=6-yi, dobije se
-z1-z2-..-z5=-10
dakle: (14 povrh 4).
e sad, neznam ni sama jel to dobro i jel se moze tako, ili je bolje jednostavno ispisat sve petorke(odmah pitanje: treba li uzet u obzir i permutacije?)?nek me netko ispravi ako sam u krivu. hvala
| ddduuu (napisa): |
Jel netko moze objasnit ovaj dio "ako zbroj brojeva koji padnu bude jednak danu njezina rodenja". Ovo je nesto iz kombinatorike, ali ne znan kako da izracunan broj kombinacija. Hvala:) |
ja sam ovo radila ovako:
A={(x1,x2,x3,x4,x5),xi e {1...6}, x1+x2+...+x5=25}
i sada sam radila kao na diskretnoj:
uvjet je 1⇐xi⇐6 pa je onda
yi=xi-1, dobije se
y1+y2+...+y5=20 i sad jos imam uvjet
yi⇐6, kale zi=6-yi, dobije se
-z1-z2-..-z5=-10
dakle: (14 povrh 4).
e sad, neznam ni sama jel to dobro i jel se moze tako, ili je bolje jednostavno ispisat sve petorke(odmah pitanje: treba li uzet u obzir i permutacije?)?nek me netko ispravi ako sam u krivu. hvala
|
|
| [Vrh] |
|
|


















