| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
NeonBlack
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (15:46:24)
Postovi: (37)16
|
 Postano: 23:33 uto, 10. 11. 2009 Naslov: Postano: 23:33 uto, 10. 11. 2009 Naslov: |
    |
|
|
dimL=1? :?
Znam to sam i napravila ako malo bolje pogledaš,ali 2 su vektora iz M,kužiš,to me zbunjuje
0, 2, 3,−1)=2(1, 0, 1,−2)+ 3(0, 1, 0, 1) + (-1)(1,−1,−2, 0)
i sad bih trebala izbaciti (-1)(1,−1,−2, 0) jer je iz L kao i (0, 2, 3,−1)
dimL=1? 
Znam to sam i napravila ako malo bolje pogledaš,ali 2 su vektora iz M,kužiš,to me zbunjuje
0, 2, 3,−1)=2(1, 0, 1,−2)+ 3(0, 1, 0, 1) + (-1)(1,−1,−2, 0)
i sad bih trebala izbaciti (-1)(1,−1,−2, 0) jer je iz L kao i (0, 2, 3,−1)
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
 Postano: 23:36 uto, 10. 11. 2009 Naslov: Postano: 23:36 uto, 10. 11. 2009 Naslov: |
    |
|
|
To sve stoji, ali sve ovo što je iz M pomnožiš i zbrojiš:
2(1, 0, 1,−2)+ 3(0, 1, 0, 1)=(2,0,2,-4)+(0,3,0,3)=(2,3,2,-1)
..pa je vektor (2,3,2,-1) baza presjeka
To sve stoji, ali sve ovo što je iz M pomnožiš i zbrojiš:
2(1, 0, 1,−2)+ 3(0, 1, 0, 1)=(2,0,2,-4)+(0,3,0,3)=(2,3,2,-1)
..pa je vektor (2,3,2,-1) baza presjeka
|
|
| [Vrh] |
|
NeonBlack
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (15:46:24)
Postovi: (37)16
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
 Postano: 9:17 sri, 11. 11. 2009 Naslov: Postano: 9:17 sri, 11. 11. 2009 Naslov: |
    |
|
|
Ako mi netko može rješiti ovaj zadatak: Neka su L i M potprostori prostora R^4 s bazama {(1,2,1,1), (1,3,2,2)} i {(1,0,-1,-1), (1,0,1,1), (2,1,1,1)} respektivno. Odreditie bazu za L presjek M.
Ako mi netko može rješiti ovaj zadatak: Neka su L i M potprostori prostora R^4 s bazama {(1,2,1,1), (1,3,2,2)} i {(1,0,-1,-1), (1,0,1,1), (2,1,1,1)} respektivno. Odreditie bazu za L presjek M.
|
|
| [Vrh] |
|
miam
Forumaš(ica)

Pridružen/a: 03. 11. 2009. (11:19:45)
Postovi: (70)16
Spol: 
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
 Postano: 10:32 sri, 11. 11. 2009 Naslov: Postano: 10:32 sri, 11. 11. 2009 Naslov: |
    |
|
|
jel mi moze neko ovo rijesiti...hvala unaprijed
A(1,0,1,0)+B(0,1,1,1)+C(1,1,1,-1)=(0,3,-2,-3)
jel mi moze neko ovo rijesiti...hvala unaprijed
A(1,0,1,0)+B(0,1,1,1)+C(1,1,1,-1)=(0,3,-2,-3)
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 10:36 sri, 11. 11. 2009 Naslov: Postano: 10:36 sri, 11. 11. 2009 Naslov: |
    |
|
|
[quote="niveus"]Ako mi netko može rješiti ovaj zadatak: Neka su L i M potprostori prostora R^4 s bazama {(1,2,1,1), (1,3,2,2)} i {(1,0,-1,-1), (1,0,1,1), (2,1,1,1)} respektivno. Odreditie bazu za L presjek M.[/quote]
[latex]\left\{ \left( 1,2,1,1\right) ,\left( 1,3,2,2\right) ,\left( 1,0,-1,-1\right) ,\left( 1,0,1,1\right) ,\left( 2,1,1,1\right)\right\}\\
\left( 1,0,-1,-1\right) =\alpha \left( 1,2,1,1\right) +\beta \left( 1,3,2,2\right) [/latex]
rjesenje je [latex]\alpha =3, \beta =-2[/latex] dakle [latex]\left( 1,0,-1,-1\right) [/latex] je u presjeku, jer je ono s ljeva iz [latex]M[/latex], a ono s dena iz [latex]L[/latex], a to je jedan teisti vektor, koji je u [latex]L[/latex] i u [latex]M[/latex], sad njega vise ne gledamo
[latex]\left( 1,0,1,1\right) =\alpha \left( 1,2,1,1\right) +\beta \left( 1,3,2,2\right) [/latex]
nema rjesenja, sto znaci da je [latex]\left( 1,0,1,1\right) [/latex] u sumi, ne u presjeku, dakle njega ostavljamo u skupu, i ostale raspisujemo i snjim
[latex]\left( 2,1,1,1\right) =\alpha \left( 1,2,1,1\right) +\beta \left( 1,3,2,2\right) +\delta \left( 1,0,1,1\right)[/latex]
ako sam dobro rjesio rjesenje je [latex]\alpha =2, \beta =-1, \delta =1[/latex] i koji je sad u presjeku pa [latex]\left( 2,1,1,1\right) -\delta \left( 1,0,1,1\right) =\alpha \left( 1,2,1,1\right) +\beta \left( 1,3,2,2\right)[/latex]
dakle bazu za presjek cine ona dva koja sam reko da su u presjeku
| niveus (napisa): | | Ako mi netko može rješiti ovaj zadatak: Neka su L i M potprostori prostora R^4 s bazama {(1,2,1,1), (1,3,2,2)} i {(1,0,-1,-1), (1,0,1,1), (2,1,1,1)} respektivno. Odreditie bazu za L presjek M. |
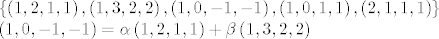
rjesenje je 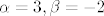 dakle dakle 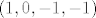 je u presjeku, jer je ono s ljeva iz je u presjeku, jer je ono s ljeva iz  , a ono s dena iz , a ono s dena iz  , a to je jedan teisti vektor, koji je u , a to je jedan teisti vektor, koji je u  i u i u  , sad njega vise ne gledamo , sad njega vise ne gledamo
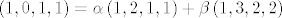
nema rjesenja, sto znaci da je 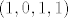 u sumi, ne u presjeku, dakle njega ostavljamo u skupu, i ostale raspisujemo i snjim u sumi, ne u presjeku, dakle njega ostavljamo u skupu, i ostale raspisujemo i snjim
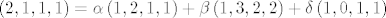
ako sam dobro rjesio rjesenje je 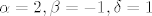 i koji je sad u presjeku pa i koji je sad u presjeku pa 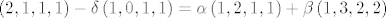
dakle bazu za presjek cine ona dva koja sam reko da su u presjeku
_________________
Mario Berljafa
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
A_je_to
Forumaš(ica)

Pridružen/a: 19. 02. 2009. (16:51:22)
Postovi: (6D)16
Spol: 
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
A_je_to
Forumaš(ica)

Pridružen/a: 19. 02. 2009. (16:51:22)
Postovi: (6D)16
Spol: 
|
 Postano: 14:13 sri, 11. 11. 2009 Naslov: Postano: 14:13 sri, 11. 11. 2009 Naslov: |
    |
|
|
Ubaciš taj p (mislim da je u ovom zadatku p=-1) u vektore a, b, c i tražiš lin. kombinaciju tj. staviš:
alfa*a+beta*b+gama*c=d, gdje su a=(1, 1, -1), b=(-1, 1, -1), c=(3, -1, 1) a d=( alfa, -1, 1).
U ovom slučaju dobiješ da sustav ima beskonačno rješenja pa to vrijedi za svaki alfa.
Ubaciš taj p (mislim da je u ovom zadatku p=-1) u vektore a, b, c i tražiš lin. kombinaciju tj. staviš:
alfa*a+beta*b+gama*c=d, gdje su a=(1, 1, -1), b=(-1, 1, -1), c=(3, -1, 1) a d=( alfa, -1, 1).
U ovom slučaju dobiješ da sustav ima beskonačno rješenja pa to vrijedi za svaki alfa.
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
gramzon
Forumaš(ica)

Pridružen/a: 09. 07. 2009. (20:11:44)
Postovi: (3B)16
Spol: 
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
marijana07
Forumaš(ica)


Pridružen/a: 30. 09. 2009. (17:51:11)
Postovi: (13)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 17:19 sri, 11. 11. 2009 Naslov: Postano: 17:19 sri, 11. 11. 2009 Naslov: |
    |
|
|
1) nadjes vektore OA, OB, OC i provjeris jesu li linearno nezavisni (preko definicije nezavisnosti, znaci mora vrijedit implikacija
aOA+bOB+cOC=0 => a=b=c=0) ako su zavisni, onda su sigurno u istoj ravnini...
2) operatore jos nismo radili
3)
ax + y= b /*(-4)
4x + ay= 2 /*a
zbrojis i dobijes
ax + y= b
(a^2-4)y = 2a -4b...
i sad imas slucajeve
[b]I) a^2-4=0[/b]
[u]a) 2a-4b!=0[/u] => nema rj.
[u]b) 2a-4b=0[/u] => a=2b, a imamo a^2 -4 =0
ako je a=2, onda je b=4 => x=(4-y)/2
ako je a=-2 => b=-4 => x= (y+4)/2
dakle u I b) dobivas jednoparametarska rjesenja
[b]II) a^2 - 4!=0[/b]
[u]a) 2a-4b=0[/u] => sustav nema rj.
[u]b) 2a-4b!=0[/u] => y= (2a-4b)/(a^2-4)
ako je a=0, onda je y=b pa u prvoj jednadzbi dobijemo
b=b... prema tome, x ne ovisi o y, pa pogledamo pocetne jednadzbe (jer smo tamo mnozili s a)
i vidimo da izgledaju ovako
y=b
4x=2 (pa dakle imamo jedinstveno rjesenje u ovisnosti o b) : y=b, x=1/2
ako je a!=0 onda imas x=(b-y)/a => opet jedinstveno
rjesenje, tj y= (2a-4b)/(a^2-4),
x= (b-2)/(a^2-4)
vektorsko-geometrijski argumenti bi valjda bili:
ako je a^2=2, 2a-4b!=0, onda su vektori (a,4) (kojeg mnozi skalar x)
i (1,a) (kojeg mnozi skalar y) kolinearni, a vektor (b,2) nije kolinearan s njima pa nema rjesenja... itd po slucajevima
1) nadjes vektore OA, OB, OC i provjeris jesu li linearno nezavisni (preko definicije nezavisnosti, znaci mora vrijedit implikacija
aOA+bOB+cOC=0 ⇒ a=b=c=0) ako su zavisni, onda su sigurno u istoj ravnini...
2) operatore jos nismo radili
3)
ax + y= b /*(-4)
4x + ay= 2 /*a
zbrojis i dobijes
ax + y= b
(a^2-4)y = 2a -4b...
i sad imas slucajeve
I) a^2-4=0
a) 2a-4b!=0 ⇒ nema rj.
b) 2a-4b=0 ⇒ a=2b, a imamo a^2 -4 =0
ako je a=2, onda je b=4 ⇒ x=(4-y)/2
ako je a=-2 ⇒ b=-4 ⇒ x= (y+4)/2
dakle u I b) dobivas jednoparametarska rjesenja
II) a^2 - 4!=0
a) 2a-4b=0 ⇒ sustav nema rj.
b) 2a-4b!=0 ⇒ y= (2a-4b)/(a^2-4)
ako je a=0, onda je y=b pa u prvoj jednadzbi dobijemo
b=b... prema tome, x ne ovisi o y, pa pogledamo pocetne jednadzbe (jer smo tamo mnozili s a)
i vidimo da izgledaju ovako
y=b
4x=2 (pa dakle imamo jedinstveno rjesenje u ovisnosti o b) : y=b, x=1/2
ako je a!=0 onda imas x=(b-y)/a ⇒ opet jedinstveno
rjesenje, tj y= (2a-4b)/(a^2-4),
x= (b-2)/(a^2-4)
vektorsko-geometrijski argumenti bi valjda bili:
ako je a^2=2, 2a-4b!=0, onda su vektori (a,4) (kojeg mnozi skalar x)
i (1,a) (kojeg mnozi skalar y) kolinearni, a vektor (b,2) nije kolinearan s njima pa nema rjesenja... itd po slucajevima
|
|
| [Vrh] |
|
marijana07
Forumaš(ica)


Pridružen/a: 30. 09. 2009. (17:51:11)
Postovi: (13)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 18:44 sri, 11. 11. 2009 Naslov: Postano: 18:44 sri, 11. 11. 2009 Naslov: |
    |
|
|
nek ti bude :D
prvi je skroz slican ko i prvi iz proslog posta:
trazimo t takav da su ova 3 vektora (a,b,c) nezavisna
stavimo ih u uvjet za nezavisnost (recimo da su skalari x,y,z):
x(5i-2j) + y(3i + 4j) + z(2i + j + (t-3)k)=0, ovo grupiramo po i, j, k i dobijemo da mora biti (jer su i,j,k nezavisni pa su skalari uz njih 0):
5x+3y+2z=0
-2x+4y+z=0
(t-3)*z =0
sad trazimo takav t da rjesenje ovog sustava bude jedinstveno, i to x=y=z=0
ocito, mora biti t!=3 (!= znaci razlicito ofc), inace mozes izabrat bilo kakav z pa ti je u 3. jednadzbi svejedno 0=0...
dakle, kad je t razlicito od 3, mora biti x=y=z=0, pa su oni vektori na pocetku nekomplanarni => baza za V3O
3) ovaj skup je sistem izvodnica, reduciramo ga do baze:
drugi vektor se ocito ne moze prikazat pomocu prvog, a 3. (kad rijesis sustav ili uocis) se moze prikazat kao 2*prvi + drugi => zavisan je => izbacimo ga i dobijemo da je baza {(1,0,-1,0),(-1,1,1,1)}
Sad nadopunimo to sa kanonskom bazom za R4
{(1,0,-1,0),(-1,1,1,1),(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1)}
Ovaj skup je ocito sistem izvodnica za R4, reduciramo ga do baze:
(neka su ovi vektori redom a,b,c,d,e,f, da ne moram pisat bas sve)
-prva 2 su nezavisna jer su bili baza za M
-odma mozes vidjet (al bolje je rjesit sustav) da se c ne moze prikazat pomocu a,b
-takodjer, d se ne moze prikazati pomocu a,b,c i to ti je dosta, jer vec imas 4 nezavisna vektora (a to je i max. moguc broj buduci si u R4), dakle znas da ce ostali bit zavisni pa ni ne moras provjeravat.
Ovime smo dobili da su a,b,c,d baza za R4, iz cega zakljucujemo da je
{c,d} baza za direktni komplement
nek ti bude 
prvi je skroz slican ko i prvi iz proslog posta:
trazimo t takav da su ova 3 vektora (a,b,c) nezavisna
stavimo ih u uvjet za nezavisnost (recimo da su skalari x,y,z):
x(5i-2j) + y(3i + 4j) + z(2i + j + (t-3)k)=0, ovo grupiramo po i, j, k i dobijemo da mora biti (jer su i,j,k nezavisni pa su skalari uz njih 0):
5x+3y+2z=0
-2x+4y+z=0
(t-3)*z =0
sad trazimo takav t da rjesenje ovog sustava bude jedinstveno, i to x=y=z=0
ocito, mora biti t!=3 (!= znaci razlicito ofc), inace mozes izabrat bilo kakav z pa ti je u 3. jednadzbi svejedno 0=0...
dakle, kad je t razlicito od 3, mora biti x=y=z=0, pa su oni vektori na pocetku nekomplanarni => baza za V3O
3) ovaj skup je sistem izvodnica, reduciramo ga do baze:
drugi vektor se ocito ne moze prikazat pomocu prvog, a 3. (kad rijesis sustav ili uocis) se moze prikazat kao 2*prvi + drugi => zavisan je => izbacimo ga i dobijemo da je baza {(1,0,-1,0),(-1,1,1,1)}
Sad nadopunimo to sa kanonskom bazom za R4
{(1,0,-1,0),(-1,1,1,1),(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1)}
Ovaj skup je ocito sistem izvodnica za R4, reduciramo ga do baze:
(neka su ovi vektori redom a,b,c,d,e,f, da ne moram pisat bas sve)
-prva 2 su nezavisna jer su bili baza za M
-odma mozes vidjet (al bolje je rjesit sustav) da se c ne moze prikazat pomocu a,b
-takodjer, d se ne moze prikazati pomocu a,b,c i to ti je dosta, jer vec imas 4 nezavisna vektora (a to je i max. moguc broj buduci si u R4), dakle znas da ce ostali bit zavisni pa ni ne moras provjeravat.
Ovime smo dobili da su a,b,c,d baza za R4, iz cega zakljucujemo da je
{c,d} baza za direktni komplement
|
|
| [Vrh] |
|
|














