| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
marijana07
Forumaš(ica)


Pridružen/a: 30. 09. 2009. (17:51:11)
Postovi: (13)16
|
|
| [Vrh] |
|
gramzon
Forumaš(ica)

Pridružen/a: 09. 07. 2009. (20:11:44)
Postovi: (3B)16
Spol: 
|
|
| [Vrh] |
|
marijana07
Forumaš(ica)


Pridružen/a: 30. 09. 2009. (17:51:11)
Postovi: (13)16
|
|
| [Vrh] |
|
miam
Forumaš(ica)

Pridružen/a: 03. 11. 2009. (11:19:45)
Postovi: (70)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 20:42 sri, 11. 11. 2009 Naslov: Postano: 20:42 sri, 11. 11. 2009 Naslov: |
    |
|
|
[quote=".anchy."]http://web.math.hr/nastava/la/kolokviji/07-08/la1/kol1b.pdf
može 4.zadatak? zbunjuje me..skroz..
pod a nije,jel? zbog onog nešto=1. :)
a kako pod b?[/quote]
Pod a) nije, jer, npr. x^3+x^2 i x+1 se nalaze u dotičnom skupu, ali njihova suma ne.
Pod b) jest. Možeš izraziti a i b preko c i d, zatim pokazati zatvorenost na dvočlane lin. komb.
| .anchy. (napisa): | http://web.math.hr/nastava/la/kolokviji/07-08/la1/kol1b.pdf
može 4.zadatak? zbunjuje me..skroz..
pod a nije,jel? zbog onog nešto=1. 
a kako pod b? |
Pod a) nije, jer, npr. x^3+x^2 i x+1 se nalaze u dotičnom skupu, ali njihova suma ne.
Pod b) jest. Možeš izraziti a i b preko c i d, zatim pokazati zatvorenost na dvočlane lin. komb.
|
|
| [Vrh] |
|
marichuy
Forumaš(ica)

Pridružen/a: 11. 11. 2009. (21:52:56)
Postovi: (26)16
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 22:20 sri, 11. 11. 2009 Naslov: Postano: 22:20 sri, 11. 11. 2009 Naslov: |
    |
|
|
[quote="pmli"]
Pod b) jest. Možeš izraziti a i b preko c i d, zatim pokazati zatvorenost na dvočlane lin. komb.[/quote]
možeš molim te napisat postupak? već se pol sata mučim,ali neznam kak da dokažem da je potprostor..
znam da uzmem 2 polinoma iz tog potrpostora,i gledam dal je njihov zbroj isto iz njega,al kak da to tu upotrijebim?
i za bazu..to isto neznam.. mislim,inače znam,ali na ovom primjeru ne! :cry: isto tak s dokazivanjem da je potprostor..
| pmli (napisa): |
Pod b) jest. Možeš izraziti a i b preko c i d, zatim pokazati zatvorenost na dvočlane lin. komb. |
možeš molim te napisat postupak? već se pol sata mučim,ali neznam kak da dokažem da je potprostor..
znam da uzmem 2 polinoma iz tog potrpostora,i gledam dal je njihov zbroj isto iz njega,al kak da to tu upotrijebim?
i za bazu..to isto neznam.. mislim,inače znam,ali na ovom primjeru ne!  isto tak s dokazivanjem da je potprostor.. isto tak s dokazivanjem da je potprostor..
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
marichuy
Forumaš(ica)

Pridružen/a: 11. 11. 2009. (21:52:56)
Postovi: (26)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
marichuy
Forumaš(ica)

Pridružen/a: 11. 11. 2009. (21:52:56)
Postovi: (26)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
marichuy
Forumaš(ica)

Pridružen/a: 11. 11. 2009. (21:52:56)
Postovi: (26)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
marichuy
Forumaš(ica)

Pridružen/a: 11. 11. 2009. (21:52:56)
Postovi: (26)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 0:29 čet, 12. 11. 2009 Naslov: Postano: 0:29 čet, 12. 11. 2009 Naslov: |
    |
|
|
Neka su [latex](z_1,z_2),(w_1,w_2) \in M[/latex] proizvoljni vektori i [latex]\alpha,\beta \in \mathbb{C}[/latex] proizvoljni skalari.Provjerimo je li [latex]\alpha (z_1,z_2) + \beta (w_1,w_2) \in M[/latex]. Vrijedi:
[latex]\alpha (z_1,z_2) + \beta (w_1,w_2) = (\alpha z_1 + \beta w_1, \alpha z_2 + \beta w_2)[/latex]
Imamo:
[latex]\overline{\alpha z_1 + \beta w_1} + i(\alpha z_2 + \beta w_2) = \overline{\alpha}\ \overline{z_1} + \alpha i z_2 + \overline{\beta}\ \overline{w_1} + \beta i w_2[/latex]
Vidimo da [latex]M[/latex] nije potprostor za kompleksne skalare, ali je za realne.
Nađimo bazu za [latex]M \leqslant \mathbb{C}^2(\mathbb{R})[/latex].
Neka je [latex](z_1,z_2) \in M[/latex] proizvoljan vektor. Neka je [latex]z_1=a_1+i b_1[/latex] i [latex]z_2=a_2+i b_2[/latex]. Vrijedi:
[latex]\overline{z_1}+i z_2 = a_1 - i b_1 + i a_2 - b_2 = 0[/latex]
Izrazimo, npr. [latex]b_2[/latex]:
[latex]b_2 = a_1 - i b_1 + i a_2[/latex]
Dobimo da je [latex](z_1,z_2) = (a_1 + i b_1,a_2+i b_2) = (a_1 + i b_1, i a_1 + b_1) = (a_1, i a_1) + (i b_1, b_1) = a_1 (1,i) + b_1(i,1)[/latex]
Dakle, skup [latex]\{(1,i),(i,1)\}[/latex] je sustav izvodnica za [latex]M[/latex].
Još dokaži da je i lin. nez., i onda znaš da je dimenzija 2.
A sad, laku noć :zzz:
Neka su 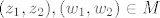 proizvoljni vektori i proizvoljni vektori i 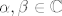 proizvoljni skalari.Provjerimo je li proizvoljni skalari.Provjerimo je li 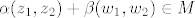 . Vrijedi: . Vrijedi:
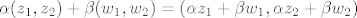
Imamo:

Vidimo da  nije potprostor za kompleksne skalare, ali je za realne. nije potprostor za kompleksne skalare, ali je za realne.
Nađimo bazu za 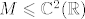 . .
Neka je 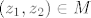 proizvoljan vektor. Neka je proizvoljan vektor. Neka je 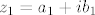 i i 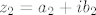 . Vrijedi: . Vrijedi:
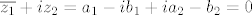
Izrazimo, npr. 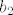 : :

Dobimo da je 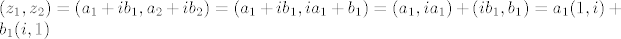
Dakle, skup 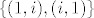 je sustav izvodnica za je sustav izvodnica za  . .
Još dokaži da je i lin. nez., i onda znaš da je dimenzija 2.
A sad, laku noć 
|
|
| [Vrh] |
|
|













