| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
markotron
Forumaš(ica)

Pridružen/a: 26. 10. 2008. (12:07:29)
Postovi: (95)16
Spol: 
Lokacija: Umag
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 14:48 sub, 5. 12. 2009 Naslov: Postano: 14:48 sub, 5. 12. 2009 Naslov: |
    |
|
|
nisam bas to proucavao... vjerojatnost je bila zanimljivija :D
al, [latex]k[/latex] i tako ne ovisi o [latex]t[/latex], onaj limes je neki linearan opeartor, i on djeluje na [latex]k[/latex] pa dobis neki vektor
valjda bi trebao dobit isti vektor ako gledas vektore koje dobis kad neki operator(o uvisnosti od [latex]t[/latex]) djeluje na neki fiksni vektor(npr [latex]k[/latex]) pa pustis limes po [latex]t[/latex]...
meni se tako cini ok, nadam se samo da nisam reko neku preveliku glupost, ipak, fali preciznosti :lol:
nisam bas to proucavao... vjerojatnost je bila zanimljivija 
al,  i tako ne ovisi o i tako ne ovisi o  , onaj limes je neki linearan opeartor, i on djeluje na , onaj limes je neki linearan opeartor, i on djeluje na  pa dobis neki vektor pa dobis neki vektor
valjda bi trebao dobit isti vektor ako gledas vektore koje dobis kad neki operator(o uvisnosti od  ) djeluje na neki fiksni vektor(npr ) djeluje na neki fiksni vektor(npr  ) pa pustis limes po ) pa pustis limes po  ... ...
meni se tako cini ok, nadam se samo da nisam reko neku preveliku glupost, ipak, fali preciznosti 
_________________
Mario Berljafa
|
|
| [Vrh] |
|
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
 Postano: 15:31 sub, 5. 12. 2009 Naslov: Postano: 15:31 sub, 5. 12. 2009 Naslov: |
    |
|
|
Dobro pitanje. Ne znam postoji li laksa argumentacija, ali cini mi se da je kljucno da su linearni operatori na KDVP neprekidne funkcije.
To se dokazuje koristeci normu operatora (koju smo spomenuli na vjezbama), a koja za operatore na KDVP uvijek postoji (koristi se konacna dimenzionalnost).
Evo ovaj dio koji vas muci. Oznacimo operatore
[latex] A_t=\frac{Df(c+te_i)-Df(c)}{t}[/latex].
Neka je [latex] A :I \rightarrow L(\mathbb{R}^n)[/latex] preslikavanje zadano s [latex] A(t)=A_t [/latex], gdje vam je I neki interval oko 0.
Vas muci zasto je [latex] (\lim_{t\rightarrow 0} A_t)k=\lim_{t\rightarrow 0} (A_tk) [/latex].
Cinjenica da je f dvaput diferencijabilna u tocki c osigurava neprekidnost od A u 0 (postoji limes [latex] \lim_{t\rightarrow 0} A_t=D^2f(c)e_i [/latex]).
Oznacimo s [latex] f_k(t)=A_tk[/latex]. Tvrdim da je za fiksan k funkcija f_k neprekidna u 0. Dokaz ide koristeci nejednakost za normu operatora
[latex] \|f_k(t)-f_k(0)\|=\|(A_t-A_0)k\|\leq \|A_t-A_0\|\| k \| [/latex].
Za dani [latex]\varepsilon >0[/latex] mozete naci delta koji vam je dobar za [latex]\varepsilon/ \|k\|[/latex] za funkciju A (koja je neprekidna u 0), pa ce vam taj delta biti dobar za funkciju f_k prema gornjoj nejednakosti.
Dakle, f_k je neprekidna u 0 po t, pa komutira s limesom:
[latex] (\lim_{t\rightarrow 0} A_t)k = A_0 k =f_k(0)= f_k(\lim_{t\rightarrow 0} t)=\lim_{t\rightarrow 0} f_k(t)=\lim_{t\rightarrow 0} (A_tk) [/latex]
Ako cete imati jos kakvih pitanja, slobodno se javite poslije vjezbi, nije mi se dalo pisati sve u latex-u.
Dobro pitanje. Ne znam postoji li laksa argumentacija, ali cini mi se da je kljucno da su linearni operatori na KDVP neprekidne funkcije.
To se dokazuje koristeci normu operatora (koju smo spomenuli na vjezbama), a koja za operatore na KDVP uvijek postoji (koristi se konacna dimenzionalnost).
Evo ovaj dio koji vas muci. Oznacimo operatore
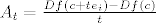 . .
Neka je 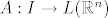 preslikavanje zadano s preslikavanje zadano s 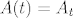 , gdje vam je I neki interval oko 0. , gdje vam je I neki interval oko 0.
Vas muci zasto je 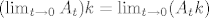 . .
Cinjenica da je f dvaput diferencijabilna u tocki c osigurava neprekidnost od A u 0 (postoji limes 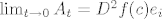 ). ).
Oznacimo s 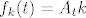 . Tvrdim da je za fiksan k funkcija f_k neprekidna u 0. Dokaz ide koristeci nejednakost za normu operatora . Tvrdim da je za fiksan k funkcija f_k neprekidna u 0. Dokaz ide koristeci nejednakost za normu operatora
 . .
Za dani 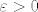 mozete naci delta koji vam je dobar za mozete naci delta koji vam je dobar za 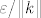 za funkciju A (koja je neprekidna u 0), pa ce vam taj delta biti dobar za funkciju f_k prema gornjoj nejednakosti. za funkciju A (koja je neprekidna u 0), pa ce vam taj delta biti dobar za funkciju f_k prema gornjoj nejednakosti.
Dakle, f_k je neprekidna u 0 po t, pa komutira s limesom:
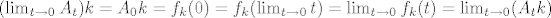
Ako cete imati jos kakvih pitanja, slobodno se javite poslije vjezbi, nije mi se dalo pisati sve u latex-u.
_________________  |
|
| [Vrh] |
|
markotron
Forumaš(ica)

Pridružen/a: 26. 10. 2008. (12:07:29)
Postovi: (95)16
Spol: 
Lokacija: Umag
|
|
| [Vrh] |
|
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
|
| [Vrh] |
|
markotron
Forumaš(ica)

Pridružen/a: 26. 10. 2008. (12:07:29)
Postovi: (95)16
Spol: 
Lokacija: Umag
|
|
| [Vrh] |
|
markotron
Forumaš(ica)

Pridružen/a: 26. 10. 2008. (12:07:29)
Postovi: (95)16
Spol: 
Lokacija: Umag
|
 Postano: 15:36 ned, 6. 12. 2009 Naslov: Postano: 15:36 ned, 6. 12. 2009 Naslov: |
    |
|
|
malo sam dokazivao i došao do nečeg:
Dakle znamo:
[latex]\lim_{x \to c}{ \frac{f_i(x)-f_i(c)-Df_i(c)(x-c)}{||x-c||} } = 0, \forall i = 1, ..., m.[/latex]
Želim pokazati da je
[latex]\lim_{x \to c}{ \frac{f(x)-f(c)-Df(c)(x-c)}{||x-c||} } = 0[/latex]
Raspisujem
[latex]\lim_{x \to c}{ \frac{f(x)-f(c)-Df(c)(x-c)}{||x-c||} } = [/latex]
[latex]\lim_{x \to c}{ \left[\frac{ 1 }{||x-c||} (f_1(x)-f_1(c)-Df_1(c)(x-c), ..., f_m(x)-f_m(c)-Df_m(c)(x-c) )\right] } =[/latex]
[latex]\lim_{x \to c}{ (\frac{f_1(x)-f_1(c)-Df_1(c)(x-c)}{||x-c||}, ..., \frac{f_m(x)-f_m(c)-Df_m(c)(x-c)}{||x-c||}) } =[/latex]
[latex]\left(\lim_{x \to c}{\frac{f_1(x)-f_1(c)-Df_1(c)(x-c)}{||x-c||}}, ...,\lim_{x \to c}{\frac{f_m(x)-f_m(c)-Df_m(c)(x-c)}{||x-c||}}\right)
= (0, ..., 0)[/latex]
Pa je i norama od toga 0.
malo sam dokazivao i došao do nečeg:
Dakle znamo:
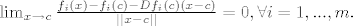
Želim pokazati da je
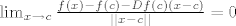
Raspisujem
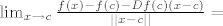
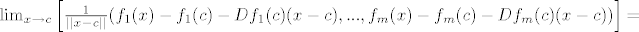
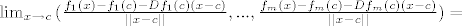
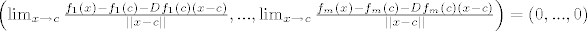
Pa je i norama od toga 0.
_________________
reductio ad absurdum
|
|
| [Vrh] |
|
ToMeK
Forumaš(ica)

Pridružen/a: 12. 09. 2008. (17:22:06)
Postovi: (BA)16
Spol: 
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
|











