| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ananas
Forumaš(ica)

Pridružen/a: 28. 10. 2009. (17:56:24)
Postovi: (34)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 13:14 pon, 18. 1. 2010 Naslov: Postano: 13:14 pon, 18. 1. 2010 Naslov: |
    |
|
|
iz grupe koja je odgovarala u 8:
1) dokazat Bolzano-Weierstrass 2. dio (tj da neprekidna funkcija na segmentu postize min, max)
2) dokaz da monotona i ogr. funkcija ima lim u +besk
3) dokaz da je monotona f. koja slika interval u interval ujedno i neprekidna
4) dokaz da su cauchyevi nizovi kvg. i obratno
5) dokaz da su cauchyeva i nizovska definicija limesa funkcije ekvivalentne
edit @spot:
pa nije bas sve mene, nebi ostale imo sta pitat inace :D... kod nas je vise manje svako dobio po jedno pitanje za pocetak, pa ak je dobro super, a ak ne onda dalje...
iz grupe koja je odgovarala u 8:
1) dokazat Bolzano-Weierstrass 2. dio (tj da neprekidna funkcija na segmentu postize min, max)
2) dokaz da monotona i ogr. funkcija ima lim u +besk
3) dokaz da je monotona f. koja slika interval u interval ujedno i neprekidna
4) dokaz da su cauchyevi nizovi kvg. i obratno
5) dokaz da su cauchyeva i nizovska definicija limesa funkcije ekvivalentne
edit @spot:
pa nije bas sve mene, nebi ostale imo sta pitat inace  ... kod nas je vise manje svako dobio po jedno pitanje za pocetak, pa ak je dobro super, a ak ne onda dalje... ... kod nas je vise manje svako dobio po jedno pitanje za pocetak, pa ak je dobro super, a ak ne onda dalje...
Zadnja promjena: pbakic; 16:28 pon, 18. 1. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
spot137
Forumaš(ica)
Pridružen/a: 02. 11. 2009. (13:33:18)
Postovi: (55)16
Spol: 
|
|
| [Vrh] |
|
some_dude
Forumaš(ica)
Pridružen/a: 08. 11. 2009. (16:23:13)
Postovi: (59)16
Spol: 
Lokacija: Zd-Zg
|
 Postano: 14:42 pon, 18. 1. 2010 Naslov: Postano: 14:42 pon, 18. 1. 2010 Naslov: |
    |
|
|
Odgovarao sam kod prof. Guljaša. Pitao me dokaz neprekidnosti x^2, BW teorem 1. i 3. tvrdnja i teorem kada je f-ja monotona na intervalu I i I'=f(I) otvoren interval pa je tada f neprekidna na I.
Ostale je pitao primjere konvergencije nizova, primjere neprekidnosti f-ja, dokaz surjektivnosti eksponencijalne, neprekidnosti eksp., neprekidnost sinusa, kosinusa, tangensa...
Odgovarao sam kod prof. Guljaša. Pitao me dokaz neprekidnosti x^2, BW teorem 1. i 3. tvrdnja i teorem kada je f-ja monotona na intervalu I i I'=f(I) otvoren interval pa je tada f neprekidna na I.
Ostale je pitao primjere konvergencije nizova, primjere neprekidnosti f-ja, dokaz surjektivnosti eksponencijalne, neprekidnosti eksp., neprekidnost sinusa, kosinusa, tangensa...
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 17:33 pon, 18. 1. 2010 Naslov: Postano: 17:33 pon, 18. 1. 2010 Naslov: |
    |
|
|
@suza, eve: Hvala, drago mi je to čuti :).
@pajopatak: Očito ne znam što je prof. Guljaš pitao u vezi tog limesa, ali ako je pitao dokaz njegove konvergentnosti (preko dokazivanja ograničenosti odozgo i monotonosti), to možeš naći na str. 49. skripte, zajedno s još nekim svojstvima tog limesa.
@smajl: Ne znam ima li toga u skripti i, ako ima, gdje se može naći, ali taj dokaz bi trebao biti dosta lagan, samo se koristi definicija supremuma i rastućosti. Aha! Evo ga, 65. i 66. stranica u skripti :).
@suza, eve: Hvala, drago mi je to čuti  . .
@pajopatak: Očito ne znam što je prof. Guljaš pitao u vezi tog limesa, ali ako je pitao dokaz njegove konvergentnosti (preko dokazivanja ograničenosti odozgo i monotonosti), to možeš naći na str. 49. skripte, zajedno s još nekim svojstvima tog limesa.
@smajl: Ne znam ima li toga u skripti i, ako ima, gdje se može naći, ali taj dokaz bi trebao biti dosta lagan, samo se koristi definicija supremuma i rastućosti. Aha! Evo ga, 65. i 66. stranica u skripti  . .
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 19:22 pon, 18. 1. 2010 Naslov: Postano: 19:22 pon, 18. 1. 2010 Naslov: |
    |
|
|
@eve: Sad se ipak već malo prezanosimo, ali hvala anyway :).
@pajopatak: Dobro, očito je numeracija u skripti koju ti imaš i u onoj [url=http://web.math.hr/~guljas/skripte/MATANALuR.pdf]na Internetu[/url] nešto drugačija, u "mom" je slučaju taj primjer na stranici 49 :). Što je pisac htio reći morat ćeš prvenstveno pitati pisca :), samo bih htio napomenuti da ovo "da se nađe limes niza tog, to bi trebalo bit onda e" nema baš nužno previše smisla, budući da je limes tog niza definiran upravo kao [latex]e[/latex] (postoje i druge ekvivalentne definicije za [latex]e[/latex], ali mislm da se ova koristi na MA1). Najbolje što možemo je, zapravo, dokazati da taj limes postoji, a dalje bi nekim drugim metodama išli tražiti preciznije koliko on iznosi (a taj dio svakako ne ulazi u gradivo MA1).
Uglavnom, da, imaš pravo ovaj dokaz se ne čini baš najjednostavniji. Prof. Šikić je (i vjerojatno još uvijek) izvodio malo drugačiji dokaz konvergencije tog niza, ali se u biti svodilo na isto, samo što se uopće nije, ako se ne varam, spominjao niz [latex](b_n)_n[/latex] - ne znam je li taj dokaz zapravo bitno jednostavniji :?.
@eve: Sad se ipak već malo prezanosimo, ali hvala anyway  . .
@pajopatak: Dobro, očito je numeracija u skripti koju ti imaš i u onoj na Internetu nešto drugačija, u "mom" je slučaju taj primjer na stranici 49  . Što je pisac htio reći morat ćeš prvenstveno pitati pisca . Što je pisac htio reći morat ćeš prvenstveno pitati pisca  , samo bih htio napomenuti da ovo "da se nađe limes niza tog, to bi trebalo bit onda e" nema baš nužno previše smisla, budući da je limes tog niza definiran upravo kao , samo bih htio napomenuti da ovo "da se nađe limes niza tog, to bi trebalo bit onda e" nema baš nužno previše smisla, budući da je limes tog niza definiran upravo kao  (postoje i druge ekvivalentne definicije za (postoje i druge ekvivalentne definicije za  , ali mislm da se ova koristi na MA1). Najbolje što možemo je, zapravo, dokazati da taj limes postoji, a dalje bi nekim drugim metodama išli tražiti preciznije koliko on iznosi (a taj dio svakako ne ulazi u gradivo MA1). , ali mislm da se ova koristi na MA1). Najbolje što možemo je, zapravo, dokazati da taj limes postoji, a dalje bi nekim drugim metodama išli tražiti preciznije koliko on iznosi (a taj dio svakako ne ulazi u gradivo MA1).
Uglavnom, da, imaš pravo ovaj dokaz se ne čini baš najjednostavniji. Prof. Šikić je (i vjerojatno još uvijek) izvodio malo drugačiji dokaz konvergencije tog niza, ali se u biti svodilo na isto, samo što se uopće nije, ako se ne varam, spominjao niz 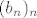 - ne znam je li taj dokaz zapravo bitno jednostavniji - ne znam je li taj dokaz zapravo bitno jednostavniji  . .
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
piccola
Forumaš(ica)

Pridružen/a: 30. 11. 2009. (15:39:50)
Postovi: (D7)16
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
jkrstic
Forumaš(ica)


Pridružen/a: 01. 10. 2009. (19:28:31)
Postovi: (AC)16
Spol: 
Lokacija: Somewhere in time
|
|
| [Vrh] |
|
piccola
Forumaš(ica)

Pridružen/a: 30. 11. 2009. (15:39:50)
Postovi: (D7)16
|
|
| [Vrh] |
|
some_dude
Forumaš(ica)
Pridružen/a: 08. 11. 2009. (16:23:13)
Postovi: (59)16
Spol: 
Lokacija: Zd-Zg
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
|

















