| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
filipnet
Forumaš(ica)


Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol: 
Lokacija: cvrsto na stolici
|
 Postano: 10:29 uto, 26. 1. 2010 Naslov: Zadatak sa roka 01.10.2009. Postano: 10:29 uto, 26. 1. 2010 Naslov: Zadatak sa roka 01.10.2009. |
    |
|
|
Bok svima, jel mi može netko pomoći oko ovog zadatka, razbijam glavu na njemu vec par dana, znam da je nesto lagano, ali nikak da skuzim. Ja sam izracunao da je permutacija reda 4, al kak dalje?
Bok svima, jel mi može netko pomoći oko ovog zadatka, razbijam glavu na njemu vec par dana, znam da je nesto lagano, ali nikak da skuzim. Ja sam izracunao da je permutacija reda 4, al kak dalje?
_________________  Everything happens with a reason! 
 |
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 12:14 uto, 26. 1. 2010 Naslov: Re: Zadatak sa roka 01.10.2009. Postano: 12:14 uto, 26. 1. 2010 Naslov: Re: Zadatak sa roka 01.10.2009. |
    |
|
|
[quote="filipnet"]Bok svima, jel mi može netko pomoći oko ovog zadatka, razbijam glavu na njemu vec par dana, znam da je nesto lagano, ali nikak da skuzim. Ja sam izracunao da je permutacija reda 4, al kak dalje?[/quote]
Ako je [latex]\sigma[/latex] permutacija reda 4, onda je [latex]\{e,\sigma,\sigma^2,\sigma^3\}[/latex] podgrupa. I ocito je najmanja podgrupa koja sadrži [latex]\sigma[/latex]. Pa je po definiciji ta podgrupa jednaka [latex]\langle\sigma\rangle[/latex].
| filipnet (napisa): | | Bok svima, jel mi može netko pomoći oko ovog zadatka, razbijam glavu na njemu vec par dana, znam da je nesto lagano, ali nikak da skuzim. Ja sam izracunao da je permutacija reda 4, al kak dalje? |
Ako je  permutacija reda 4, onda je permutacija reda 4, onda je 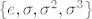 podgrupa. I ocito je najmanja podgrupa koja sadrži podgrupa. I ocito je najmanja podgrupa koja sadrži  . Pa je po definiciji ta podgrupa jednaka . Pa je po definiciji ta podgrupa jednaka 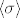 . .
|
|
| [Vrh] |
|
filipnet
Forumaš(ica)


Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol: 
Lokacija: cvrsto na stolici
|
 Postano: 22:30 uto, 26. 1. 2010 Naslov: Re: Zadatak sa roka 01.10.2009. Postano: 22:30 uto, 26. 1. 2010 Naslov: Re: Zadatak sa roka 01.10.2009. |
    |
|
|
[quote="rafaelm"]
Ako je [latex]\sigma[/latex] permutacija reda 4, onda je [latex]\{e,\sigma,\sigma^2,\sigma^3\}[/latex] podgrupa. I ocito je najmanja podgrupa koja sadrži [latex]\sigma[/latex]. Pa je po definiciji ta podgrupa jednaka [latex]\langle\sigma\rangle[/latex].[/quote]
pretpostavljam da je e identiteta, jedino me buni, dal gledam sigme u ciklusu koji je reda 4, pa od tamo vucem ostale sigme?
Jer u ovom primjeru, imamo dva ciklusa (1,3) i (2,4,6,5), pa bi onda sigma bio{e, 2,4,6} zar ne?
| rafaelm (napisa): |
Ako je  permutacija reda 4, onda je permutacija reda 4, onda je 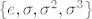 podgrupa. I ocito je najmanja podgrupa koja sadrži podgrupa. I ocito je najmanja podgrupa koja sadrži  . Pa je po definiciji ta podgrupa jednaka . Pa je po definiciji ta podgrupa jednaka 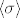 . . |
pretpostavljam da je e identiteta, jedino me buni, dal gledam sigme u ciklusu koji je reda 4, pa od tamo vucem ostale sigme?
Jer u ovom primjeru, imamo dva ciklusa (1,3) i (2,4,6,5), pa bi onda sigma bio{e, 2,4,6} zar ne?
_________________  Everything happens with a reason! 
 |
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 23:50 uto, 26. 1. 2010 Naslov: Re: Zadatak sa roka 01.10.2009. Postano: 23:50 uto, 26. 1. 2010 Naslov: Re: Zadatak sa roka 01.10.2009. |
    |
|
|
[quote="filipnet"][quote="rafaelm"]
Ako je [latex]\sigma[/latex] permutacija reda 4, onda je [latex]\{e,\sigma,\sigma^2,\sigma^3\}[/latex] podgrupa. I ocito je najmanja podgrupa koja sadrži [latex]\sigma[/latex]. Pa je po definiciji ta podgrupa jednaka [latex]\langle\sigma\rangle[/latex].[/quote]
pretpostavljam da je e identiteta, jedino me buni, dal gledam sigme u ciklusu koji je reda 4, pa od tamo vucem ostale sigme?
Jer u ovom primjeru, imamo dva ciklusa (1,3) i (2,4,6,5), pa bi onda sigma bio{e, 2,4,6} zar ne?[/quote]
Ne. Sigma je samo jedna, to je ona permutacija koja ti je zadana, nema "ostalih sigma". Taj zadatak sam ja imao na pismenom i poanta je bila da se [latex]\sigma[/latex] potencira dok se ne dođe do identitete. Budući je [latex]\sigma^4=id[/latex], dovoljno je bilo napisati [latex]\left\langle\sigma\right\rangle=\{id,\sigma,\sigma^2,\sigma^3\}[/latex] i možda kratko obrazložiti zašto je to tako (nešto kao ono što je rafaelm napisao).
| filipnet (napisa): | | rafaelm (napisa): |
Ako je  permutacija reda 4, onda je permutacija reda 4, onda je 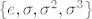 podgrupa. I ocito je najmanja podgrupa koja sadrži podgrupa. I ocito je najmanja podgrupa koja sadrži  . Pa je po definiciji ta podgrupa jednaka . Pa je po definiciji ta podgrupa jednaka 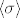 . . |
pretpostavljam da je e identiteta, jedino me buni, dal gledam sigme u ciklusu koji je reda 4, pa od tamo vucem ostale sigme?
Jer u ovom primjeru, imamo dva ciklusa (1,3) i (2,4,6,5), pa bi onda sigma bio{e, 2,4,6} zar ne? |
Ne. Sigma je samo jedna, to je ona permutacija koja ti je zadana, nema "ostalih sigma". Taj zadatak sam ja imao na pismenom i poanta je bila da se  potencira dok se ne dođe do identitete. Budući je potencira dok se ne dođe do identitete. Budući je 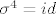 , dovoljno je bilo napisati , dovoljno je bilo napisati 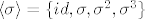 i možda kratko obrazložiti zašto je to tako (nešto kao ono što je rafaelm napisao). i možda kratko obrazložiti zašto je to tako (nešto kao ono što je rafaelm napisao).
_________________
The Dude Abides
Zadnja promjena: goranm; 23:53 uto, 26. 1. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 23:52 uto, 26. 1. 2010 Naslov: Re: Zadatak sa roka 01.10.2009. Postano: 23:52 uto, 26. 1. 2010 Naslov: Re: Zadatak sa roka 01.10.2009. |
    |
|
|
[quote="filipnet"]pretpostavljam da je e identiteta, jedino me buni, dal gledam sigme u ciklusu koji je reda 4, pa od tamo vucem ostale sigme?
Jer u ovom primjeru, imamo dva ciklusa (1,3) i (2,4,6,5), pa bi onda sigma bio{e, 2,4,6} zar ne?[/quote]
[latex]e[/latex] je identiteta. Ne shvacam baš što te muči. Grupa generirana jednim elementom je uvjek ciklička, te sastoji se od svih potencija generatora. Dakle, zadanu permutaciju [latex]\sigma[/latex] samo kvadriraš i kubiraš (dalje ne moraš jer kažeš da je reda 4). Grupa generirana sa [latex]\sigma[/latex] sastoji se od neutralnog elementa, [latex]\sigma[/latex], i potencija.
| filipnet (napisa): | pretpostavljam da je e identiteta, jedino me buni, dal gledam sigme u ciklusu koji je reda 4, pa od tamo vucem ostale sigme?
Jer u ovom primjeru, imamo dva ciklusa (1,3) i (2,4,6,5), pa bi onda sigma bio{e, 2,4,6} zar ne? |
 je identiteta. Ne shvacam baš što te muči. Grupa generirana jednim elementom je uvjek ciklička, te sastoji se od svih potencija generatora. Dakle, zadanu permutaciju je identiteta. Ne shvacam baš što te muči. Grupa generirana jednim elementom je uvjek ciklička, te sastoji se od svih potencija generatora. Dakle, zadanu permutaciju  samo kvadriraš i kubiraš (dalje ne moraš jer kažeš da je reda 4). Grupa generirana sa samo kvadriraš i kubiraš (dalje ne moraš jer kažeš da je reda 4). Grupa generirana sa  sastoji se od neutralnog elementa, sastoji se od neutralnog elementa,  , i potencija. , i potencija.
|
|
| [Vrh] |
|
filipnet
Forumaš(ica)


Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol: 
Lokacija: cvrsto na stolici
|
|
| [Vrh] |
|
|










