| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 13:03 pon, 23. 3. 2009 Naslov: Postano: 13:03 pon, 23. 3. 2009 Naslov: |
    |
|
|
Pretpostavljam da matrica koju si napisao već je Jordanova forma neke matrice A, možeš li prepisati tu matricu čija se Jordanova forma i baza traže? :)
Jer u suprotnom, ako se traži Jordanova baza te matrice koju si dao kao primjer, tada ta matrica već ima Jordanov oblik pa je jedna Jordanova baza kanonska baza [latex](e_1,e_2,e_3,e_4)[/latex].:)
No svejedno, ako je matrica iz primjera Jordanova forma neke matrice A, tada se za svojstvenu vrijednost -3 formira tablica
[latex]\begin{array}{rcl}
\ker{B_{-3}^2}\dot{-}\ker{B_{-3}} & \vline & f_2\\
\hline
\ker{B_{-3}} & \vline & f_1
\end{array}[/latex]
Sada trebaš izračunati jezgru operatora [latex]B_{-3}=A-(-3)I[/latex] i jezgru operatora [latex]B_{-3}^2[/latex]. Kada to izračunaš, trebaš naći bazu [latex]\{f_2\}[/latex] potprostora [latex]P[/latex] za kojeg vrijedi [latex]\ker{B_{-3}}\dot{+}P=\ker{B_{-3}^2}[/latex]. Kada pronađeš tu bazu, tada si našao i [latex]f_2[/latex], a [latex]f_1[/latex] lako izračunaš kao [latex]f_1=B_{-3}f_2[/latex].
Na isit način računaš za svojstvenu vrijednost 2. Sada tablica ovako izgleda:
[latex]\begin{array}{rcl}
\ker{B_{2}^2}\dot{-}\ker{B_{2}} & \vline & f_4\\
\hline
\ker{B_{2}} & \vline & f_3
\end{array}[/latex]
Kada izračunaš [latex]f_1[/latex], [latex]f_2[/latex], [latex]f_3[/latex] i [latex]f_4[/latex], jedna Jordanova baza biti će uređena četvorka [latex](f_1,f_2,f_3,f_4)[/latex].
Ako želiš provjeriti da li je baza dobra, tada formiraš matricu S tako da u i-ti stupac upišeš vektor [latex]f_i[/latex] i izračunaš [latex]SJS^{-1}[/latex]. Ako je sve bilo dobro, trebao bi dobiti matricu čija se Jordanova forma i baza traži.
Uglavnom, algoritam je dosta šablonski, samo nije najjasniji iz jednog primjera jer tablice za svojstvene vrijednosti ovise o Jordanovoj formi, tj. dimenzijama klijetki za svojstvene vrijednosti.
Pretpostavljam da matrica koju si napisao već je Jordanova forma neke matrice A, možeš li prepisati tu matricu čija se Jordanova forma i baza traže? 
Jer u suprotnom, ako se traži Jordanova baza te matrice koju si dao kao primjer, tada ta matrica već ima Jordanov oblik pa je jedna Jordanova baza kanonska baza 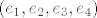 . .
No svejedno, ako je matrica iz primjera Jordanova forma neke matrice A, tada se za svojstvenu vrijednost -3 formira tablica
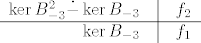
Sada trebaš izračunati jezgru operatora 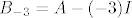 i jezgru operatora i jezgru operatora 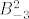 . Kada to izračunaš, trebaš naći bazu . Kada to izračunaš, trebaš naći bazu 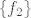 potprostora potprostora  za kojeg vrijedi za kojeg vrijedi 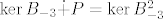 . Kada pronađeš tu bazu, tada si našao i . Kada pronađeš tu bazu, tada si našao i 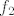 , a , a 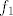 lako izračunaš kao lako izračunaš kao 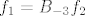 . .
Na isit način računaš za svojstvenu vrijednost 2. Sada tablica ovako izgleda:
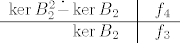
Kada izračunaš 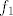 , , 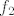 , , 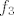 i i 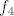 , jedna Jordanova baza biti će uređena četvorka , jedna Jordanova baza biti će uređena četvorka 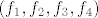 . .
Ako želiš provjeriti da li je baza dobra, tada formiraš matricu S tako da u i-ti stupac upišeš vektor 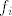 i izračunaš i izračunaš 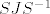 . Ako je sve bilo dobro, trebao bi dobiti matricu čija se Jordanova forma i baza traži. . Ako je sve bilo dobro, trebao bi dobiti matricu čija se Jordanova forma i baza traži.
Uglavnom, algoritam je dosta šablonski, samo nije najjasniji iz jednog primjera jer tablice za svojstvene vrijednosti ovise o Jordanovoj formi, tj. dimenzijama klijetki za svojstvene vrijednosti.
_________________
The Dude Abides
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 17:36 pon, 23. 3. 2009 Naslov: Postano: 17:36 pon, 23. 3. 2009 Naslov: |
    |
|
|
Sigurno je dobro prepisana prva matrica? Jer spektar te matrice koju si napisao je {-3, 1+Sqrt(2),1-Sqrt(2)}, a trebao bi biti {-3,1}. :)
Raspisati ću drugi primjer. Računanje ranga, jezgre i ostalih stvari neću raspisivati, preko Mathematice ću računati.
Sudeći po mathematici, Jordanova forma za taj primjer je kriva, pa i to da napravim:
Karakteristični polinom matrice A je [latex](\lambda+2)^4[/latex] pa je spektar {-2}. Budući je kratnost od -2 u karakterističnom polinomu jednaka 4, tada je [latex]dim V_{-2}=4[/latex].
Računamo [latex]d(B_{-2}=A+2I)[/latex]. Rang od [latex]B_{-2}[/latex] je 2 pa je defekt 2 što nije jednako [latex]dim V_{-2}=4[/latex].
Računamo [latex]d(B_{-2}^2)[/latex]. Rang je 0 pa je defekt 4. Tu stajemo.
Zato što smo za svojstvenu vrijednost -2 ovaj postupak dva puta provodili, tada zaključujemo da je minimalni polinom [latex](\lambda+2)^2[/latex].
Sada definiramo [latex]d_k^{(\lambda)}=d(B_{\lambda}^k)[/latex]. Mi smo računali defekt za [latex]\lambda=-2[/latex] i [latex]k=1,2[/latex].
Sada je:
[latex]d_0^{(-2)}=0\\
d_1^{(-2)}=2\\
d_2^{(-2)}=4\\
[/latex]
Svaki idući [latex]d_k^{(-2)}[/latex] je očito 4. Kako smo za [latex]B_{-2}[/latex] dva puta tražili defekt, tada možemo imati klijetke dimenzije 1 i/ili dimenzije 2 pa računamo koliko takvih ima:
[latex]n_1=4-4-0=0\\
n_2=8-2-4=2.
[/latex]
Dakle, Jordanova forma za matricu A je oblika
[latex]\left(
\begin{array}{cccc}
-2 & 1 & 0 & 0 \\
0 & -2 & 0 & 0 \\
0 & 0 & -2 & 1 \\
0 & 0 & 0 & -2
\end{array}\right)
[/latex]
Tablica za svojstvenu vrijednost -2 je dana sa
[latex]
\begin{array}{cccc}
\ker{B_{-2}^2}\dot{-}\ker{B_{-2}} & \vline & f_2 & f_4\\
\hline
\ker{B_{-2}} & \vline & f_1 & f_3
\end{array}
[/latex]
Krećemo odozgo tablice, tj. tražimo bazu [latex]\{f_2,f_4\}[/latex] potprostora [latex]P[/latex] tako da vrijedi [latex]\ker{B_{-2}}\dot{+}P=\ker{B_{-2}^2}[/latex] pa moramo izračunati jezgre tih operatora.
Vrijedi:
[latex]\ker{B_{-2}}=[\{(0,1,-1,1),(1,0,0,0)\}]\\
\ker{B_{-2}^2}=[\{(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1)\}]
[/latex]
Sada ti trebaju bilo koja dva nezavisna vektora koji [b]nisu[/b] u [latex]\ker{B_{-2}}[/latex], ali tako da sa vektorima iz [latex]\ker{B_{-2}}[/latex] daju [latex]\ker{B_{-2}^2}[/latex].
Kada takva dva nađeš, vrijediti će [latex]f_1=B_{-2}f_2[/latex] i [latex]f_3=B_{-2}f_4[/latex] (to iščitaš iz tablice; ako je [latex]f_k[/latex] u istom stupcu i jedan redak ispod kao [latex]f_j[/latex], tada je [latex]f_k=B_\lambda f_j[/latex])
Sada je tvoja Jordanova baza uređena četvorka vektora [latex](f_1, f_2, f_3, f_4)[/latex]. :)
Malo sam se žurio pa ne stignem dovršiti i nadam se da nisam neku nepotrebnu katastroficu umetnuo. :)
Sigurno je dobro prepisana prva matrica? Jer spektar te matrice koju si napisao je {-3, 1+Sqrt(2),1-Sqrt(2)}, a trebao bi biti {-3,1}. 
Raspisati ću drugi primjer. Računanje ranga, jezgre i ostalih stvari neću raspisivati, preko Mathematice ću računati.
Sudeći po mathematici, Jordanova forma za taj primjer je kriva, pa i to da napravim:
Karakteristični polinom matrice A je 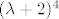 pa je spektar {-2}. Budući je kratnost od -2 u karakterističnom polinomu jednaka 4, tada je pa je spektar {-2}. Budući je kratnost od -2 u karakterističnom polinomu jednaka 4, tada je 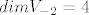 . .
Računamo 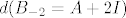 . Rang od . Rang od 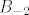 je 2 pa je defekt 2 što nije jednako je 2 pa je defekt 2 što nije jednako 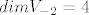 . .
Računamo 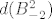 . Rang je 0 pa je defekt 4. Tu stajemo. . Rang je 0 pa je defekt 4. Tu stajemo.
Zato što smo za svojstvenu vrijednost -2 ovaj postupak dva puta provodili, tada zaključujemo da je minimalni polinom 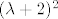 . .
Sada definiramo 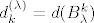 . Mi smo računali defekt za . Mi smo računali defekt za 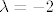 i i 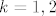 . .
Sada je:
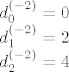
Svaki idući 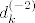 je očito 4. Kako smo za je očito 4. Kako smo za 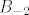 dva puta tražili defekt, tada možemo imati klijetke dimenzije 1 i/ili dimenzije 2 pa računamo koliko takvih ima: dva puta tražili defekt, tada možemo imati klijetke dimenzije 1 i/ili dimenzije 2 pa računamo koliko takvih ima:
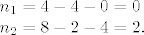
Dakle, Jordanova forma za matricu A je oblika

Tablica za svojstvenu vrijednost -2 je dana sa
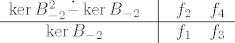
Krećemo odozgo tablice, tj. tražimo bazu 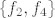 potprostora potprostora  tako da vrijedi tako da vrijedi 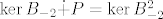 pa moramo izračunati jezgre tih operatora. pa moramo izračunati jezgre tih operatora.
Vrijedi:
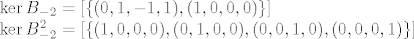
Sada ti trebaju bilo koja dva nezavisna vektora koji nisu u 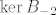 , ali tako da sa vektorima iz , ali tako da sa vektorima iz 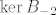 daju daju 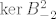 . .
Kada takva dva nađeš, vrijediti će 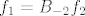 i i 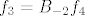 (to iščitaš iz tablice; ako je (to iščitaš iz tablice; ako je 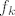 u istom stupcu i jedan redak ispod kao u istom stupcu i jedan redak ispod kao 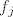 , tada je , tada je 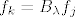 ) )
Sada je tvoja Jordanova baza uređena četvorka vektora 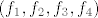 . . 
Malo sam se žurio pa ne stignem dovršiti i nadam se da nisam neku nepotrebnu katastroficu umetnuo. 
_________________
The Dude Abides
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Glupko_3.14
Forumaš(ica)


Pridružen/a: 27. 09. 2007. (10:32:16)
Postovi: (77)16
|
|
| [Vrh] |
|
Željan
Forumaš(ica)
Pridružen/a: 10. 03. 2010. (22:37:50)
Postovi: (6)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Željan
Forumaš(ica)
Pridružen/a: 10. 03. 2010. (22:37:50)
Postovi: (6)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 22:24 pon, 15. 3. 2010 Naslov: Postano: 22:24 pon, 15. 3. 2010 Naslov: |
    |
|
|
S obzirom da je (1,0,0,0) u obje jezgre, njega sigurno ne bih birao. Ako zanemarimo nulvektor, iz (1,0,0,0) i (0,1,-1,1) linearnim kombinacijama mogu dobiti samo vektore kojima su sve koordinate različite od nule pa bih, jednostavnosti radi, birao dva vektora koji su linearno nezavisni i imaju ili samo jednu ili dvije koordinate različite od nule, npr. (0,0,0,1) i (0,0,1,1).
Sada metodama iz linearne algebre provjeriš da li su vektori (1,0,0,0), (0,1,-1,1), (0,0,0,1) i (0,0,1,1) linearno nezavisni. Ako jesu, našao si svoja dva vektora jer bilo koja 4 linearno nezavisna vektora će razapinjati [latex]\mathbb{R}^4=\ker{B_{-2}^2}[/latex]. Ako nisu linearno nezavisni, probaš sa neka druga dva vektora.
S obzirom da je (1,0,0,0) u obje jezgre, njega sigurno ne bih birao. Ako zanemarimo nulvektor, iz (1,0,0,0) i (0,1,-1,1) linearnim kombinacijama mogu dobiti samo vektore kojima su sve koordinate različite od nule pa bih, jednostavnosti radi, birao dva vektora koji su linearno nezavisni i imaju ili samo jednu ili dvije koordinate različite od nule, npr. (0,0,0,1) i (0,0,1,1).
Sada metodama iz linearne algebre provjeriš da li su vektori (1,0,0,0), (0,1,-1,1), (0,0,0,1) i (0,0,1,1) linearno nezavisni. Ako jesu, našao si svoja dva vektora jer bilo koja 4 linearno nezavisna vektora će razapinjati 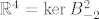 . Ako nisu linearno nezavisni, probaš sa neka druga dva vektora. . Ako nisu linearno nezavisni, probaš sa neka druga dva vektora.
_________________
The Dude Abides
Zadnja promjena: goranm; 2:15 uto, 16. 3. 2010; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
Željan
Forumaš(ica)
Pridružen/a: 10. 03. 2010. (22:37:50)
Postovi: (6)16
|
|
| [Vrh] |
|
|












