| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
piccola
Forumaš(ica)

Pridružen/a: 30. 11. 2009. (15:39:50)
Postovi: (D7)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 21:12 ned, 4. 4. 2010 Naslov: Postano: 21:12 ned, 4. 4. 2010 Naslov: |
    |
|
|
[latex]\left[ \left\{ \begin{bmatrix} -1 \\ 0 \\ 1 \end{bmatrix} \right\} \right][/latex], [latex]\left[ \left\{ \begin{bmatrix} -2 \\ 1 \\ 0 \end{bmatrix} \right\} \right][/latex] i [latex]\left[ \left\{ \begin{bmatrix} 0 \\ -1 \\ 1 \end{bmatrix} \right\} \right][/latex].
Za ubuduće, preporučam funkciju Eigenvectors za Wolfram Alphu/Mathematicu. U ovom slučaju, poziv je Eigenvectors[{{-1,2,2},{2,2,2},{-3,-6,-6}}].
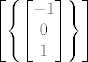 , , 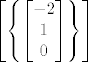 i i  . .
Za ubuduće, preporučam funkciju Eigenvectors za Wolfram Alphu/Mathematicu. U ovom slučaju, poziv je Eigenvectors[{{-1,2,2},{2,2,2},{-3,-6,-6}}].
|
|
| [Vrh] |
|
ankovacic
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (19:28:17)
Postovi: (5C)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 15:43 pon, 5. 4. 2010 Naslov: Postano: 15:43 pon, 5. 4. 2010 Naslov: |
    |
|
|
dobi li se u 3.zadatku matrica {(1,-1,-8 ),(0,1,7),(0,0,-1)}?
i samo pitanje,kako da dokažem da je ta matrica inverz matričnog prikaza od A u toj istoj bazi?
dobi li se u 3.zadatku matrica {(1,-1,-8 ),(0,1,7),(0,0,-1)}?
i samo pitanje,kako da dokažem da je ta matrica inverz matričnog prikaza od A u toj istoj bazi?
|
|
| [Vrh] |
|
genchy
Forumaš(ica)

Pridružen/a: 03. 09. 2009. (18:32:56)
Postovi: (29)16
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
kikyca
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (18:45:07)
Postovi: (32)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
kikyca
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (18:45:07)
Postovi: (32)16
Spol: 
|
|
| [Vrh] |
|
dina12
Forumaš(ica)

Pridružen/a: 21. 11. 2009. (17:20:26)
Postovi: (18)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
 Postano: 21:38 pon, 5. 4. 2010 Naslov: Postano: 21:38 pon, 5. 4. 2010 Naslov: |
    |
|
|
Hmmmm.. pa uzela bazu f tj
vektor(1,1,0) pa A(1,1,0)=(2,1,0) analogno za ostale f i dobila matricu
[latex]\displaystyle [A]_f = \begin{bmatrix} 2 & 0 & 0 \\1 & -2 & 1 \\ 0 & 1 & -1 \end{bmatrix}[/latex]
Hmmmm.. pa uzela bazu f tj
vektor(1,1,0) pa A(1,1,0)=(2,1,0) analogno za ostale f i dobila matricu
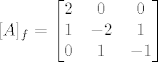
_________________
Give me a place to stand, and I will move the earth.
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 22:01 pon, 5. 4. 2010 Naslov: Postano: 22:01 pon, 5. 4. 2010 Naslov: |
    |
|
|
[quote="ajaxcy"]ali i kad izmnozim sa matricama prijelaza nikako da dobijem to sto si napisao...bili bi ti tila pre velika gnjavaza napisati kako si dosao do toga :DD plizz[/quote]
Kako svoje zadaće pišem u latex-u, to mi nije problem (samo treba par šugavih dolara maknuti). :D
[latex]e = \{(1,0,0), (0,1,0), (0,0,1)\}, [A]_e^e = \left[ \begin{array}{rrr} 1 & 1 & 0 \\ 0 & 1 & -1 \\ 0 & 0 & 1 \end{array} \right]\\
f = \{(1,1,0), (1,-1,1), (0,0,-1)\}, [A]_f^f = [I_{\mathbb{R}^3}]_e^f [A]_e^e [I_{\mathbb{R}^3}]_f^e\\
$[I_{\mathbb{R}^3}]_f^e = \left[ \begin{array}{rrr} 1 & 1 & 0 \\ 1 & -1 & 0 \\ 0 & 1 & -1 \end{array} \right]$
$\left[ \begin{array}{rrr|rrr} 1 & 1 & 0 & 1 & 0 & 0 \\ 1 & -1 & 0 & 0 & 1 & 0 \\ 0 & 1 & -1 & 0 & 0 & 1 \end{array} \right] \sim \left[ \begin{array}{rrr|rrr} 1 & 1 & 0 & 1 & 0 & 0 \\ 0 & -2 & 0 & -1 & 1 & 0 \\ 0 & 1 & -1 & 0 & 0 & 1 \end{array} \right] \sim \left[ \begin{array}{rrr|rrr} 2 & 2 & 0 & 2 & 0 & 0 \\ 0 & -2 & 0 & -1 & 1 & 0 \\ 0 & 2 & -2 & 0 & 0 & 2 \end{array} \right] \sim \left[ \begin{array}{rrr|rrr} 2 & 0 & 0 & 1 & 1 & 0 \\ 0 & -2 & 0 & -1 & 1 & 0 \\ 0 & 0 & -2 & -1 & 1 & 2 \end{array} \right]$\\
$\displaystyle \Rightarrow \ [I_{\mathbb{R}^3}]_e^f = \frac{1}{2} \left[ \begin{array}{rrr} 1 & 1 & 0 \\ 1 & -1 & 0 \\ 1 & -1 & -2 \end{array} \right]$
\begin{align*}
[A]_f^f & = \frac{1}{2} \left[ \begin{array}{rrr} 1 & 1 & 0 \\ 1 & -1 & 0 \\ 1 & -1 & -2 \end{array} \right] \left[ \begin{array}{rrr} 1 & 1 & 0 \\ 0 & 1 & -1 \\ 0 & 0 & 1 \end{array} \right] \left[ \begin{array}{rrr} 1 & 1 & 0 \\ 1 & -1 & 0 \\ 0 & 1 & -1 \end{array} \right] \\
& = \frac{1}{2} \left[ \begin{array}{rrr} 1 & 2 & -1 \\ 1 & 0 & 1 \\ 1 & 0 & -1 \end{array} \right] \left[ \begin{array}{rrr} 1 & 1 & 0 \\ 1 & -1 & 0 \\ 0 & 1 & -1 \end{array} \right] = \frac{1}{2} \left[ \begin{array}{rrr} 3 & -2 & 1 \\ 1 & 2 & -1 \\ 1 & 0 & 1 \end{array} \right]
\end{align*}[/latex]
| ajaxcy (napisa): | ali i kad izmnozim sa matricama prijelaza nikako da dobijem to sto si napisao...bili bi ti tila pre velika gnjavaza napisati kako si dosao do toga  D plizz D plizz |
Kako svoje zadaće pišem u latex-u, to mi nije problem (samo treba par šugavih dolara maknuti). 

|
|
| [Vrh] |
|
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
|
| [Vrh] |
|
|



















