| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
nike
Forumaš(ica)

Pridružen/a: 11. 02. 2010. (13:05:01)
Postovi: (58)16
|
|
| [Vrh] |
|
Alisa
Forumaš(ica)
Pridružen/a: 16. 02. 2008. (15:34:59)
Postovi: (4E)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Alisa
Forumaš(ica)
Pridružen/a: 16. 02. 2008. (15:34:59)
Postovi: (4E)16
|
|
| [Vrh] |
|
Gost
|
 Postano: 19:25 sub, 10. 4. 2010 Naslov: Postano: 19:25 sub, 10. 4. 2010 Naslov: |
    |
|
|
Ali to nema veze sa svojstvenim vrijednostima, kad izracunamo determinante glavnih minora imamo tri uvjeta, x^2>=0, 4x^2>=1 i 4x^2>=9, pa slijedi da x>3/2, znaci faktorizacija Choleskog vrijedi za svaki x>3/2, a faktorizaciju onda treba racunati s tim parametrom
Ali to nema veze sa svojstvenim vrijednostima, kad izracunamo determinante glavnih minora imamo tri uvjeta, x^2>=0, 4x^2>=1 i 4x^2>=9, pa slijedi da x>3/2, znaci faktorizacija Choleskog vrijedi za svaki x>3/2, a faktorizaciju onda treba racunati s tim parametrom
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 10:34 pon, 12. 4. 2010 Naslov: Postano: 10:34 pon, 12. 4. 2010 Naslov: |
    |
|
|
imamo neke preskočene derivacije pa nemožemo računati preko hermita i sl,nego uzmemo proizvoljan polinom p(x)=ax^3+bx^2+cx+d
imamo zadano:
f(1)=2
f''(1)=1
f''(2)=0
f'(3)=1
sada to uvrstimo u naš interpolacijski polinom(znamo da vrijedi f(x)=p(x),f'(x)=p'(x),itd)
a+b+c+d=2
6a+2b=1
12a+2b=0
27a+6b+c=1
iz čega izlazi a=-1/6 b=1 c=-1/2 d=5/3
pa je interpolacijski polinom p(x)=(-1/6)x^3+x^2+(-1/2)x+5/3
tu smo mogli dobiti slučaj da sustav nema rješenja,kao na vježbama pa takav polinom ne postoji
edit:sad kad bolje pogledam,mislim da se i prvi dio rješava na sličan način,samo što se gleda kada sustav ima jedinstveno rješenje. jer da bi interp.polinom postojao,on mora biti jedinstven..
edit2:jel ulazi u kolokvij metoda najmanjih kvadrata s predavanja?
imamo neke preskočene derivacije pa nemožemo računati preko hermita i sl,nego uzmemo proizvoljan polinom p(x)=ax^3+bx^2+cx+d
imamo zadano:
f(1)=2
f''(1)=1
f''(2)=0
f'(3)=1
sada to uvrstimo u naš interpolacijski polinom(znamo da vrijedi f(x)=p(x),f'(x)=p'(x),itd)
a+b+c+d=2
6a+2b=1
12a+2b=0
27a+6b+c=1
iz čega izlazi a=-1/6 b=1 c=-1/2 d=5/3
pa je interpolacijski polinom p(x)=(-1/6)x^3+x^2+(-1/2)x+5/3
tu smo mogli dobiti slučaj da sustav nema rješenja,kao na vježbama pa takav polinom ne postoji
edit:sad kad bolje pogledam,mislim da se i prvi dio rješava na sličan način,samo što se gleda kada sustav ima jedinstveno rješenje. jer da bi interp.polinom postojao,on mora biti jedinstven..
edit2:jel ulazi u kolokvij metoda najmanjih kvadrata s predavanja?
|
|
| [Vrh] |
|
bimar
Forumaš(ica)


Pridružen/a: 16. 11. 2008. (14:45:25)
Postovi: (61)16
Lokacija: arkadija
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
bozidarsevo
Forumaš(ica)


Pridružen/a: 17. 09. 2008. (10:15:01)
Postovi: (1D1)16
Spol: 
Lokacija: Samobor
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 15:30 pon, 12. 4. 2010 Naslov: Postano: 15:30 pon, 12. 4. 2010 Naslov: |
    |
|
|
[quote="bozidarsevo"]pitanje za Choleskog:
matrica je :
2x^2 1 0
1 2 -2
0 -2 x^2
* 2x^2*(4-2x^2)-(0-x^2) ,tj x<3/2
[/quote]
kak si ovo dobio? ne znam što su minore pa ako bi netko mogao napisati..tj.znam da su podmatrice,ali koje?
i nešto mi još nije jasno,kod interpolacije linearnim splajnom,formula glasi
p(i)(x)=(x-x(i))/(x(i-1)-x(i))*f(x(i-1))+(x-x(i-1))/(x(i)-x(i-1))*f(x(i)),
i-ovi u zagradama su indeksi.
e sad,mi interpoliramo funkciju f,a u interpolacijskom polinomu računamo vrijednost od f u nekoj točki..to mi je skroz besmisleno..ili se taj f odnosi na nešto drugo?
| bozidarsevo (napisa): | pitanje za Choleskog:
matrica je :
2x^2 1 0
1 2 -2
0 -2 x^2
* 2x^2*(4-2x^2)-(0-x^2) ,tj x<3/2
|
kak si ovo dobio? ne znam što su minore pa ako bi netko mogao napisati..tj.znam da su podmatrice,ali koje?
i nešto mi još nije jasno,kod interpolacije linearnim splajnom,formula glasi
p(i)(x)=(x-x(i))/(x(i-1)-x(i))*f(x(i-1))+(x-x(i-1))/(x(i)-x(i-1))*f(x(i)),
i-ovi u zagradama su indeksi.
e sad,mi interpoliramo funkciju f,a u interpolacijskom polinomu računamo vrijednost od f u nekoj točki..to mi je skroz besmisleno..ili se taj f odnosi na nešto drugo?
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
lorozic
Forumaš(ica)

Pridružen/a: 08. 12. 2008. (17:11:14)
Postovi: (50)16
Spol: 
|
 Postano: 16:59 pon, 12. 4. 2010 Naslov: Postano: 16:59 pon, 12. 4. 2010 Naslov: |
    |
|
|
[quote="Cobs"]u 2 zadatku di se traži aproksimacija početnim dijelom Taylorovog reda oko 0 npr. za A) dio imamo funkciju:
[latex]f(x) = x\cdot cos(x) - x[/latex]
nađem da je Taylorov red za tu funkciju:
[latex]\displaystyle{\sum_{n=1}^{\infty}(-1)^n\frac{x^{2n+1}}{(2n)!}}[/latex]
i sad vidim da za
[latex]x = 15\pi[/latex]
imam zbrajanje ( i oduzimanje ) velikih brojeva u pocetnom dijelu reda( dok ne počne padat ), međutim rezultat mi je "dosta" veliki broj po apsolutnoj vrijednosti ( oko 94 ) pa mogu reć da je ovaj red dobro aproksimira u računalnoj aritmetici!
Dal je to dovoljno dobar odgovor il još nešto trebamo napomenut?[/quote]
rezultat je 94 al je najveći član reda 10^19 (najdeš ga tak da gledaš izraz x^(2n+1) / (2n)! > x^(2n+3)/(2n+2)! tj tražiš kad članovi počnu padati).omjer ti je onda >10^17 pa je ovo loša aproksimacija jer je došlo do katastrofalnog kraćenja.
glede argumentiranja, mislim da se traži objašnjenje katastrofalnog kraćenja, neznam kaj bi drugo moglo biti.
btw dal neko zna kaj sve smijemo imati ko šalabahtere, jer bi nam dobro došli oni sa taylorom iz analize. i kakve digitrone smijemo imati?
| Cobs (napisa): | u 2 zadatku di se traži aproksimacija početnim dijelom Taylorovog reda oko 0 npr. za A) dio imamo funkciju:
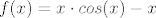
nađem da je Taylorov red za tu funkciju:
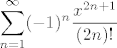
i sad vidim da za

imam zbrajanje ( i oduzimanje ) velikih brojeva u pocetnom dijelu reda( dok ne počne padat ), međutim rezultat mi je "dosta" veliki broj po apsolutnoj vrijednosti ( oko 94 ) pa mogu reć da je ovaj red dobro aproksimira u računalnoj aritmetici!
Dal je to dovoljno dobar odgovor il još nešto trebamo napomenut? |
rezultat je 94 al je najveći član reda 10^19 (najdeš ga tak da gledaš izraz x^(2n+1) / (2n)! > x^(2n+3)/(2n+2)! tj tražiš kad članovi počnu padati).omjer ti je onda >10^17 pa je ovo loša aproksimacija jer je došlo do katastrofalnog kraćenja.
glede argumentiranja, mislim da se traži objašnjenje katastrofalnog kraćenja, neznam kaj bi drugo moglo biti.
btw dal neko zna kaj sve smijemo imati ko šalabahtere, jer bi nam dobro došli oni sa taylorom iz analize. i kakve digitrone smijemo imati?
Zadnja promjena: lorozic; 17:24 pon, 12. 4. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
|








