| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
patlidzan
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (19:17:28)
Postovi: (76)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
patlidzan
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (19:17:28)
Postovi: (76)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
patlidzan
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (19:17:28)
Postovi: (76)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 22:45 pon, 12. 4. 2010 Naslov: Postano: 22:45 pon, 12. 4. 2010 Naslov: |
    |
|
|
[latex]f_1(x)=x^2,~f_2(x)=x^2-2x+3[/latex]. Traže se [latex]x_1, x_2[/latex] takvi da je [latex]k=f_1'(x_1)=f_2'(x_2)[/latex]. Iz toga slijedi [latex]x_2=x_1+1[/latex]. Jer zajednička tangenta prolazi točkama [latex](x_1,f_1(x_1)),(x_2,f_2(x_2))=(x_1+1,f_2(x_1+1))[/latex], jednadžba tangente mora biti [latex]y=2x+x_1^2-2x_1[/latex]. Iz toga slijedi da je [latex]f'(x_1)=2[/latex] pa je [latex]x_1=1[/latex], odnosno [latex]y=2x-1[/latex].
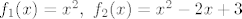 . Traže se . Traže se 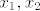 takvi da je takvi da je 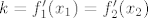 . Iz toga slijedi . Iz toga slijedi 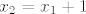 . Jer zajednička tangenta prolazi točkama . Jer zajednička tangenta prolazi točkama 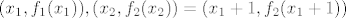 , jednadžba tangente mora biti , jednadžba tangente mora biti 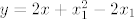 . Iz toga slijedi da je . Iz toga slijedi da je 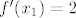 pa je pa je 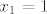 , odnosno , odnosno 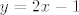 . .
_________________
The Dude Abides
|
|
| [Vrh] |
|
homesweethome
Forumaš(ica)

Pridružen/a: 21. 10. 2009. (16:25:25)
Postovi: (1C)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 14:57 sri, 21. 4. 2010 Naslov: Postano: 14:57 sri, 21. 4. 2010 Naslov: |
    |
|
|
Radi se o funkciji koja ima prekid svugdje, osim u 0 i 1.
Neprekidnost u 0 se lako pokaže koristeći [latex]\varepsilon-\delta[/latex] definiciju. Treba naći takav [latex]\delta[/latex] da, ako je [latex]|x| < \delta[/latex], onda je [latex]|f(x) - f(0)| < \varepsilon[/latex]. Ako je [latex]x \in \mathbb{R} \setminus \mathbb{Q}[/latex], tvrdnja vrijedi za bilo koji [latex]\delta[/latex]. Ako je [latex]x \in \mathbb{Q}[/latex], imamo [latex]|f(x)-f(0)| = |x^2 - x - 0| = |x||x-1| < \delta |x-1|[/latex]. Dakle, problem je ocijeniti [latex]|x-1|[/latex] odozgo (hint: [color=white]nejednakost trokuta[/color]).
Neprekidnost u 1 se vrlo slično dokazuje.
Prekidnost u točki [latex]c \in \mathbb{Q} \setminus \{0, 1\}[/latex] se vrlo jednostavno dokazuje (hint: [color=white]epsilon = |c^2 - c|/2[/color]).
Dokaz prekidnosti u točki [latex]c \in \mathbb{R} \setminus \mathbb{Q}[/latex] je pomalo trikav. Jedna ideja je iskoristiti [color=white]neprekidnost preslikavanja x -> x^2 - x[/color].
Za još hintova, javi. :D
Radi se o funkciji koja ima prekid svugdje, osim u 0 i 1.
Neprekidnost u 0 se lako pokaže koristeći 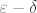 definiciju. Treba naći takav definiciju. Treba naći takav  da, ako je da, ako je  , onda je , onda je 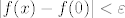 . Ako je . Ako je 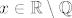 , tvrdnja vrijedi za bilo koji , tvrdnja vrijedi za bilo koji  . Ako je . Ako je 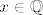 , imamo , imamo 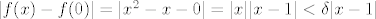 . Dakle, problem je ocijeniti . Dakle, problem je ocijeniti  odozgo (hint: nejednakost trokuta). odozgo (hint: nejednakost trokuta).
Neprekidnost u 1 se vrlo slično dokazuje.
Prekidnost u točki 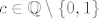 se vrlo jednostavno dokazuje (hint: epsilon = |c^2 - c|/2). se vrlo jednostavno dokazuje (hint: epsilon = |c^2 - c|/2).
Dokaz prekidnosti u točki 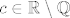 je pomalo trikav. Jedna ideja je iskoristiti neprekidnost preslikavanja x → x^2 - x. je pomalo trikav. Jedna ideja je iskoristiti neprekidnost preslikavanja x → x^2 - x.
Za još hintova, javi. 
|
|
| [Vrh] |
|
Boris B.
Forumaš(ica)

Pridružen/a: 19. 01. 2010. (18:01:54)
Postovi: (32)16
Spol: 
|
 Postano: 3:36 ned, 25. 4. 2010 Naslov: Postano: 3:36 ned, 25. 4. 2010 Naslov: |
    |
|
|
[quote="homesweethome"]jel mi moze objasniti 2. b) zad iz druge zadace... ? :) molim lijepo :)[/quote]
Prekidnost možeš dokazati i ako gledaš ovako:
1. Za svaki [latex]q \in \mathbb Q[/latex] postoji niz iracionalnih brojeva koji konvergira u njega - neka je npr. [latex]a_0 = e,\ a_n = \frac{a_{n-1}+q}{2} = \frac{e}{2^n} + q \frac{2^n-1}{2^n}[/latex] (valjda sam dobro napisao ovo zadnje, uglavnom tu je negdje, svakako ide u q) ;)
No f(q) = q^2 - q, a f(a_n) = 0, za sve n, tako da za q različit od 0 i 1 f mora imati prekid.
2. [latex]\forall c \in \mathbb R\setminus \mathbb Q[/latex] analogno uzmes niz iz Q koji konvergira u taj c. E sad, prilicno je ocito da tako sto postoji (npr. niz aproksimacija na n decimala :P), ali pretpostavljam da bi trebao dati tocnu konstrukciju takvog niza i dokazati da je konvergentna. Srecom, to se da napraviti slicno kao gore, samo treba opet paziti da svi "ociti" koraci budu argumentirani. Na kraju (uz pmlijev hint :)) opet dobivas prekidnost.
3. Pri dokazivanju neprekidnosti u 0 i 1 ovakvim pristupom stvari postaju pomalo neugodne, jer treba dokazati da [latex]\displaystyle \forall a \in \mathbb R^\mathbb N\ (\lim_n a_n = c\ \Longrightarrow\ \lim_n f(a_n) = f(c))[/latex] sto zbog ovoga ∀ i nije bas zgodno :? Al kolko vidim, moze se, iako je s epsilon-delta vjerojatno krace.
Ako nekog zanima kako tocno idu 2. i 3. dio, napisem. Ali sumnjam da hoce, posto jos jedino nasa grupa treba predati :P
| homesweethome (napisa): | jel mi moze objasniti 2. b) zad iz druge zadace... ?  molim lijepo molim lijepo  |
Prekidnost možeš dokazati i ako gledaš ovako:
1. Za svaki 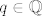 postoji niz iracionalnih brojeva koji konvergira u njega - neka je npr. postoji niz iracionalnih brojeva koji konvergira u njega - neka je npr. 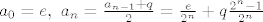 (valjda sam dobro napisao ovo zadnje, uglavnom tu je negdje, svakako ide u q) (valjda sam dobro napisao ovo zadnje, uglavnom tu je negdje, svakako ide u q) 
No f(q) = q^2 - q, a f(a_n) = 0, za sve n, tako da za q različit od 0 i 1 f mora imati prekid.
2. 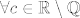 analogno uzmes niz iz Q koji konvergira u taj c. E sad, prilicno je ocito da tako sto postoji (npr. niz aproksimacija na n decimala analogno uzmes niz iz Q koji konvergira u taj c. E sad, prilicno je ocito da tako sto postoji (npr. niz aproksimacija na n decimala  ), ali pretpostavljam da bi trebao dati tocnu konstrukciju takvog niza i dokazati da je konvergentna. Srecom, to se da napraviti slicno kao gore, samo treba opet paziti da svi "ociti" koraci budu argumentirani. Na kraju (uz pmlijev hint ), ali pretpostavljam da bi trebao dati tocnu konstrukciju takvog niza i dokazati da je konvergentna. Srecom, to se da napraviti slicno kao gore, samo treba opet paziti da svi "ociti" koraci budu argumentirani. Na kraju (uz pmlijev hint  ) opet dobivas prekidnost. ) opet dobivas prekidnost.
3. Pri dokazivanju neprekidnosti u 0 i 1 ovakvim pristupom stvari postaju pomalo neugodne, jer treba dokazati da 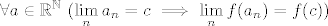 sto zbog ovoga ∀ i nije bas zgodno sto zbog ovoga ∀ i nije bas zgodno  Al kolko vidim, moze se, iako je s epsilon-delta vjerojatno krace. Al kolko vidim, moze se, iako je s epsilon-delta vjerojatno krace.
Ako nekog zanima kako tocno idu 2. i 3. dio, napisem. Ali sumnjam da hoce, posto jos jedino nasa grupa treba predati 
_________________
The lyf so short, the craft so long to lerne
|
|
| [Vrh] |
|
NeonBlack
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (15:46:24)
Postovi: (37)16
|
|
| [Vrh] |
|
suza
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (14:37:50)
Postovi: (65)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 14:22 ned, 25. 4. 2010 Naslov: Postano: 14:22 ned, 25. 4. 2010 Naslov: |
    |
|
|
2.19 d) supstitucija pa parc integracija dvaput :D
prvo supstitucija [latex]arctgx=t[/latex] , [latex]\frac{1}{1+x^2}dx=dt[/latex], [latex]x=tgt[/latex], [latex]\frac{1}{\sqrt{1+x^2}}= \frac{1}{\sqrt{1+tg^2t}}[/latex] i uvažavajući da je [latex]tgt=\frac{sint}{cost}[/latex] i [latex]sin^2t+cos^2t=1[/latex]
dobijemo
[latex]\int{sinte^tdt}[/latex] što se riješi sa dvije parc integracije (dobije se na desnoj strani isti taj integral, pa se prebaci lijevo, sigurno ste to vidjeli na vježbama)
2.19 d) supstitucija pa parc integracija dvaput 
prvo supstitucija 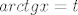 , , 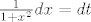 , , 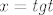 , , 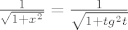 i uvažavajući da je i uvažavajući da je 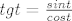 i i 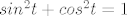
dobijemo
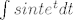 što se riješi sa dvije parc integracije (dobije se na desnoj strani isti taj integral, pa se prebaci lijevo, sigurno ste to vidjeli na vježbama) što se riješi sa dvije parc integracije (dobije se na desnoj strani isti taj integral, pa se prebaci lijevo, sigurno ste to vidjeli na vježbama)
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
|
| [Vrh] |
|
|



















