| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Wolfert
Forumaš(ica)


Pridružen/a: 24. 10. 2006. (12:27:01)
Postovi: (42)16
|
|
| [Vrh] |
|
guzonja
Gost
|
|
| [Vrh] |
|
tinker bell
Forumaš(ica)

Pridružen/a: 10. 10. 2009. (08:46:34)
Postovi: (47)16
|
|
| [Vrh] |
|
renatobab
Forumaš(ica)
Pridružen/a: 09. 02. 2010. (15:56:08)
Postovi: (6)16
|
 Postano: 16:23 ned, 9. 5. 2010 Naslov: Postano: 16:23 ned, 9. 5. 2010 Naslov: |
    |
|
|
Drugi zadatak:
Zamislimo da je zadatak rijesen. Uz oznake kao na slici lako vidimo da je [latex]\triangle HBC[/latex] slican [latex]\triangle ABC[/latex] pa je kut [latex]\alpha = \angle CAB \cong \angle HCB[/latex]. S druge strane, za tezisnicu nad hipotenuzom vrijedi [latex]2t=c[/latex], pa je [latex]\tiangle AMC[/latex] jednakokracan, tj [latex]\angle CAB \cong \angle MCA[/latex]. Kako je pravac [latex]MC[/latex] simetrala pravog kuta to su kutevi [latex]\angle DCM \cong \angle HCD = \frac{\pi}{4}-\alpha[/latex]. Sada se lako vidi i da je [latex]\angle MDC = \frac{3\pi}{4}-\alpha[/latex].
Oznacimo sada [latex]e = d(M,D), f= d(D,H), v = d(H,C), t = d(M,C)[/latex].
Iz [latex]\triangle DHC[/latex] imamo [latex]\tan({\frac{\pi}{4}-\alpha})=\frac{f}{v}[/latex].
Iz [latex]\triangle MDC[/latex] citamo [latex]\frac{\sin({\frac{\pi}{4}-\alpha})}{\sin({\frac{3\pi}{4}-\alpha})}=\frac{e}{t}[/latex].
Sto daje [latex]\frac{e}{t} = \frac{f}{v}[/latex].
Nadalje [latex]\triangle MHC[/latex] je pravokutan pa vrijedi [latex]t^2=v^2+x^2[/latex], sto, kada supstituiramo po [latex]v[/latex] u gornji omjer, dobivamo:
[latex]v=\frac{fx}{\sqrt{e^2-f^2}}[/latex].
Sada se [latex]v[/latex] lako konstruira kao cetvrta proporcionala.
Ostaje konstruirati okomicu u [latex]N[/latex], nanjeti [latex]v[/latex] nebili dobili tocku [latex]C[/latex], te spustiti tezisnicu na dani pravac, sa svake strane tocke [latex]M[/latex].
Trokut je jednistven do na orjentaciju, rijesenja nece biti kada je [latex]e < f[/latex] ili [latex] D \cong H \neq M[/latex] kada se trokut degenerira, dok ce u slucaju [latex]M\cong D \cong H [/latex] postojati, neizmjerno mnogo rijesenja.
Drugi zadatak:
Zamislimo da je zadatak rijesen. Uz oznake kao na slici lako vidimo da je 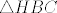 slican slican 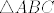 pa je kut pa je kut 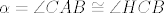 . S druge strane, za tezisnicu nad hipotenuzom vrijedi . S druge strane, za tezisnicu nad hipotenuzom vrijedi 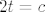 , pa je , pa je 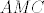 jednakokracan, tj jednakokracan, tj  . Kako je pravac . Kako je pravac 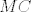 simetrala pravog kuta to su kutevi simetrala pravog kuta to su kutevi 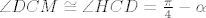 . Sada se lako vidi i da je . Sada se lako vidi i da je 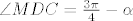 . .
Oznacimo sada 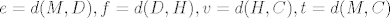 . .
Iz 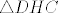 imamo imamo 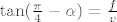 . .
Iz 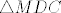 citamo citamo 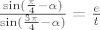 . .
Sto daje  . .
Nadalje 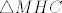 je pravokutan pa vrijedi je pravokutan pa vrijedi 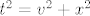 , sto, kada supstituiramo po , sto, kada supstituiramo po  u gornji omjer, dobivamo: u gornji omjer, dobivamo:
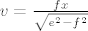 . .
Sada se  lako konstruira kao cetvrta proporcionala. lako konstruira kao cetvrta proporcionala.
Ostaje konstruirati okomicu u  , nanjeti , nanjeti  nebili dobili tocku nebili dobili tocku  , te spustiti tezisnicu na dani pravac, sa svake strane tocke , te spustiti tezisnicu na dani pravac, sa svake strane tocke  . .
Trokut je jednistven do na orjentaciju, rijesenja nece biti kada je 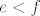 ili ili 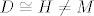 kada se trokut degenerira, dok ce u slucaju kada se trokut degenerira, dok ce u slucaju 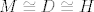 postojati, neizmjerno mnogo rijesenja. postojati, neizmjerno mnogo rijesenja.
| Description: |
|

Download |
| Filename: |
zad2.zip |
| Filesize: |
7.53 KB |
| Downloaded: |
107 Time(s) |
|
|
| [Vrh] |
|
mery
Forumaš(ica)

Pridružen/a: 01. 12. 2008. (21:57:21)
Postovi: (43)16
|
|
| [Vrh] |
|
renatobab
Forumaš(ica)
Pridružen/a: 09. 02. 2010. (15:56:08)
Postovi: (6)16
|
 Postano: 18:47 ned, 9. 5. 2010 Naslov: Postano: 18:47 ned, 9. 5. 2010 Naslov: |
    |
|
|
Treci zadatak:
Konstruirajmo prvo [latex]\triangle M_a H_a A[/latex] kojem je [latex]t_a[/latex] hipotenuza, a [latex]v_a[/latex] jedna kateta.
Iz povrsine znamo da je [latex]a\cdot v_a = b \cdot v_b[/latex], odnosno udaljenosti do tocke [latex]C[/latex] moraju biti u omjeru [latex]\frac{d(M_a,C)}{d(A,C)}=\frac{v_b}{2v_a}[/latex].
Sada znamo konstruirati ovakvo geometrijsko mjesto tocaka [latex]C[/latex] (kruznica), tamo gdje se ova kruznica sijece sa pravcem [latex]M_a H_a[/latex] je trazena tocka [latex]C[/latex].
Jedino jos preostaje prenjeti [latex]d(M_a,C)[/latex] na drugu stranu nebi li dobili tocku [latex]B[/latex].
U slucaju da smo prenjeli tocku [latex]M_a[/latex] na drugu stranu dobili bi isti trokut samo suprotno orijentiran.
Treci zadatak:
Konstruirajmo prvo 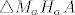 kojem je kojem je 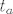 hipotenuza, a hipotenuza, a 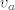 jedna kateta. jedna kateta.
Iz povrsine znamo da je 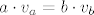 , odnosno udaljenosti do tocke , odnosno udaljenosti do tocke  moraju biti u omjeru moraju biti u omjeru 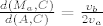 . .
Sada znamo konstruirati ovakvo geometrijsko mjesto tocaka  (kruznica), tamo gdje se ova kruznica sijece sa pravcem (kruznica), tamo gdje se ova kruznica sijece sa pravcem 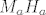 je trazena tocka je trazena tocka  . .
Jedino jos preostaje prenjeti 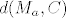 na drugu stranu nebi li dobili tocku na drugu stranu nebi li dobili tocku  . .
U slucaju da smo prenjeli tocku 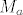 na drugu stranu dobili bi isti trokut samo suprotno orijentiran. na drugu stranu dobili bi isti trokut samo suprotno orijentiran.
| Description: |
|

Download |
| Filename: |
zad3.zip |
| Filesize: |
8.46 KB |
| Downloaded: |
113 Time(s) |
|
|
| [Vrh] |
|
bernhard
Forumaš(ica)

Pridružen/a: 23. 03. 2010. (20:38:33)
Postovi: (6E)16
Lokacija: Multiple users - od 2012 profil iskljucivo koristi Maria Culjak
|
|
| [Vrh] |
|
renatobab
Forumaš(ica)
Pridružen/a: 09. 02. 2010. (15:56:08)
Postovi: (6)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Antonija
Forumaš(ica)


Pridružen/a: 04. 11. 2007. (09:38:06)
Postovi: (139)16
|
|
| [Vrh] |
|
Bug
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: 
Lokacija: Kako kad!!
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
renatobab
Forumaš(ica)
Pridružen/a: 09. 02. 2010. (15:56:08)
Postovi: (6)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 1:51 pon, 10. 5. 2010 Naslov: Postano: 1:51 pon, 10. 5. 2010 Naslov: |
    |
|
|
Da, to je ta ideja, ali ti konstrukcija nije dorađena, pa ti se u jednom trenutku sve raspadne i nemaš više jednakostranični, nego jednakokračni trokut. To se riješi na način da rotiraš i manju i veću kružnicu. Jednu za [latex]+\frac{\pi}{3}[/latex], drugu za [latex]-\frac{\pi}{3}[/latex].
Da, to je ta ideja, ali ti konstrukcija nije dorađena, pa ti se u jednom trenutku sve raspadne i nemaš više jednakostranični, nego jednakokračni trokut. To se riješi na način da rotiraš i manju i veću kružnicu. Jednu za 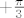 , drugu za , drugu za 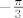 . .
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
|
|
| [Vrh] |
|
renatobab
Forumaš(ica)
Pridružen/a: 09. 02. 2010. (15:56:08)
Postovi: (6)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
mery
Forumaš(ica)

Pridružen/a: 01. 12. 2008. (21:57:21)
Postovi: (43)16
|
|
| [Vrh] |
|
niky
Forumaš(ica)
Pridružen/a: 04. 11. 2008. (17:08:33)
Postovi: (2F)16
|
|
| [Vrh] |
|
:)
Forumaš(ica)
Pridružen/a: 25. 04. 2009. (16:17:14)
Postovi: (66)16
|
|
| [Vrh] |
|
1122
Gost
|
|
| [Vrh] |
|
|







