| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
 Postano: 12:28 ned, 30. 5. 2010 Naslov: Postano: 12:28 ned, 30. 5. 2010 Naslov: |
    |
|
|
Mislim da je netko već pisao, ali nema veze, probat ću ja objasnit, bog mi pomogo :D
Znači, danu bazu za potprostor M ortonormiraš GS postupkom, pa ćeš dobit prikaz matrice na sljedeći način:
[latex]A = \alpha_{1}E_{1}+\alpha_{2}E_{2}+...+\alpha_{9}E_{9}[/latex], gdje [latex]\{E_{1},E_{2}\}[/latex] ortonormirana baza za potprostor M.
Sada slijedi da ove [latex]\alpha{1},\alpha{2}[/latex] dobiješ kao [latex]\alpha_{1}=<A,E_{1}>,\ \alpha_{2}=<A,E_{2}>[/latex] zbog ornormiranosti baze.
Tako onda lagano dobiješ [latex]B = \alpha_{1}E_{1}+\alpha_{2}E_{2}\in M[/latex], pa iz toga i C = A-B.
Mislim da to bi to trebalo bit dobro :D
Mislim da je netko već pisao, ali nema veze, probat ću ja objasnit, bog mi pomogo 
Znači, danu bazu za potprostor M ortonormiraš GS postupkom, pa ćeš dobit prikaz matrice na sljedeći način:
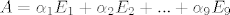 , gdje , gdje 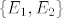 ortonormirana baza za potprostor M. ortonormirana baza za potprostor M.
Sada slijedi da ove 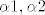 dobiješ kao dobiješ kao 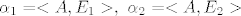 zbog ornormiranosti baze. zbog ornormiranosti baze.
Tako onda lagano dobiješ 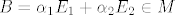 , pa iz toga i C = A-B. , pa iz toga i C = A-B.
Mislim da to bi to trebalo bit dobro 
|
|
| [Vrh] |
|
A_je_to
Forumaš(ica)

Pridružen/a: 19. 02. 2009. (16:51:22)
Postovi: (6D)16
Spol: 
|
|
| [Vrh] |
|
some_dude
Forumaš(ica)
Pridružen/a: 08. 11. 2009. (16:23:13)
Postovi: (59)16
Spol: 
Lokacija: Zd-Zg
|
 Postano: 14:03 ned, 30. 5. 2010 Naslov: Postano: 14:03 ned, 30. 5. 2010 Naslov: |
    |
|
|
[quote="A_je_to"]Kako izgleda baza za M ortogonalni komplement u 2. zad. Hvala!
http://web.math.hr/nastava/la/kolokviji/06-07/la2/kol2b.pdf[/quote]
{ (-1,1,-1,0), (0,0,0,1) }
{ (-1,1,-1,0), (0,0,0,1) }
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
c4rimson
Forumaš(ica)

Pridružen/a: 11. 01. 2010. (18:57:26)
Postovi: (3B)16
|
|
| [Vrh] |
|
suza
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (14:37:50)
Postovi: (65)16
Spol: 
|
|
| [Vrh] |
|
c4rimson
Forumaš(ica)

Pridružen/a: 11. 01. 2010. (18:57:26)
Postovi: (3B)16
|
|
| [Vrh] |
|
michelangelo
Forumaš(ica)

Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
c4rimson
Forumaš(ica)

Pridružen/a: 11. 01. 2010. (18:57:26)
Postovi: (3B)16
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
 Postano: 19:27 ned, 30. 5. 2010 Naslov: Postano: 19:27 ned, 30. 5. 2010 Naslov: |
    |
|
|
[quote="kaj"][quote="smajl"]Koje se rjesenje dobije u 2. zadatku? http://web.math.hr/nastava/la/kolokviji/07-08/la2/kol2a.pdf
Vidjela sam da se na pocetku raspravljalo o tom zadatku, a mene samo zanima rjesenje... hvala :lol:[/quote]
A koje je tvoje rješenje ?[/quote]
stavila sam da mi je B=alfaA1+betaA2, a C=A-B i dobila sam da mi je beta= -82/79, a alfa=-406/117 (nije mi se do dalo kratit, ak je moguce), sto mi se cini kao krivo rjesenje :cry: pa nisam dalje racunala B i C :?
Sad sam skuzila da sam krivo nesto izmnozila, pa sam sad dobila da mi je beta=-1 a alfa=2, jel to onda dobro?
| kaj (napisa): |
A koje je tvoje rješenje ? |
stavila sam da mi je B=alfaA1+betaA2, a C=A-B i dobila sam da mi je beta= -82/79, a alfa=-406/117 (nije mi se do dalo kratit, ak je moguce), sto mi se cini kao krivo rjesenje  pa nisam dalje racunala B i C pa nisam dalje racunala B i C 
Sad sam skuzila da sam krivo nesto izmnozila, pa sam sad dobila da mi je beta=-1 a alfa=2, jel to onda dobro?
|
|
| [Vrh] |
|
NeonBlack
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (15:46:24)
Postovi: (37)16
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
 Postano: 21:22 ned, 30. 5. 2010 Naslov: Postano: 21:22 ned, 30. 5. 2010 Naslov: |
    |
|
|
Prvo G.S. A1 i A2. , alfa = <A,F1>, beta = <A,F2>, gdje su F1 i F2 ortonormirani elementi iz M. C = A - B , A nam je zadan, a B je alfa*F1 + beta*F2.
Prvo G.S. A1 i A2. , alfa = <A,F1>, beta = <A,F2>, gdje su F1 i F2 ortonormirani elementi iz M. C = A - B , A nam je zadan, a B je alfa*F1 + beta*F2.
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
|














