| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Tvrtko
Forumaš(ica)

Pridružen/a: 21. 10. 2006. (12:12:34)
Postovi: (10A)16
Lokacija: CCP 4345 / PMF-MO 225
|
 Postano: 17:14 uto, 27. 4. 2010 Naslov: Postano: 17:14 uto, 27. 4. 2010 Naslov: |
    |
|
|
[quote="Tygy"]
Nadalje, npr 2. zadatak pola nas nije znalo ni počet jer smo zaboravili od proslog semestra kako se traže rjesenja one jednadžbe, trebali su nas bar upozorit na takve stvari...
[/quote]
Da vidimo... Prvo sto se trazilo u zadatku je bilo koliko rjesenja ima jednadzba
[latex]x+y+z=3024[/latex]
u skupu prirodnih brojeva. (Druga grupa je imala slicno.)
Na vjezbama se radi apsolutno isti primjer u opcenitoj formi tj. koliko rjesenja ima jednadzba
[latex]x_1+x_2+\ldots+x_r=n[/latex]
u skupu prirodnih brojeva (pritom je [latex]r\leq n[/latex]).
Rjesenja ove jednadzbe ima kao sto je tamo vec obrazlozeno [latex]\binom{n-1}{r-1}[/latex].
Dakle drugim rijecima pocetna jednadzba ima [latex]\binom{3023}{2}[/latex] rjesenja. To je pocetak koji nosi 3 boda (2 boda ako ste napravili neku gresku, tipa zaboravili da ne dopustamo 0 da budu rjesenja.)
Ako nasumce odaberemo rješenje (x',y',z') jednadžbe kolika je vjerojatnost da brojevi x', y', z' pri dijeljenju s 3 daju ostatak 1?
Tada je x'=3x_0+1, y'=3y_0+1, z'=3z_0+1, gdje x_0,y_0,z_0 mogu biti iz [latex]\mathbb{N}_0[/latex]. (Slicnog stimanja da uvjeti jednakosti budu zadovoljeni je bilo na vjezbama.) Uvrstimo u pocetnu jednadzbu i dobivamo
[latex]3x_0+1+3y_0+1+3z_0+1=3024.[/latex]
tada je
[latex]x_0+y_0+z_0=1007.[/latex]
Ova jednakost ima (prema zadatku na vježbama) rješenja [latex]\binom{1009}{2}[/latex] (ovdje i 0 moze biti rjesenje).
Trazena vjerojatnost je [latex]\binom{1009}{2}/\binom{3023}{2}.[/latex]
| Tygy (napisa): |
Nadalje, npr 2. zadatak pola nas nije znalo ni počet jer smo zaboravili od proslog semestra kako se traže rjesenja one jednadžbe, trebali su nas bar upozorit na takve stvari...
|
Da vidimo... Prvo sto se trazilo u zadatku je bilo koliko rjesenja ima jednadzba
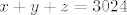
u skupu prirodnih brojeva. (Druga grupa je imala slicno.)
Na vjezbama se radi apsolutno isti primjer u opcenitoj formi tj. koliko rjesenja ima jednadzba

u skupu prirodnih brojeva (pritom je 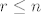 ). ).
Rjesenja ove jednadzbe ima kao sto je tamo vec obrazlozeno 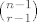 . .
Dakle drugim rijecima pocetna jednadzba ima 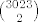 rjesenja. To je pocetak koji nosi 3 boda (2 boda ako ste napravili neku gresku, tipa zaboravili da ne dopustamo 0 da budu rjesenja.) rjesenja. To je pocetak koji nosi 3 boda (2 boda ako ste napravili neku gresku, tipa zaboravili da ne dopustamo 0 da budu rjesenja.)
Ako nasumce odaberemo rješenje (x',y',z') jednadžbe kolika je vjerojatnost da brojevi x', y', z' pri dijeljenju s 3 daju ostatak 1?
Tada je x'=3x_0+1, y'=3y_0+1, z'=3z_0+1, gdje x_0,y_0,z_0 mogu biti iz 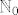 . (Slicnog stimanja da uvjeti jednakosti budu zadovoljeni je bilo na vjezbama.) Uvrstimo u pocetnu jednadzbu i dobivamo . (Slicnog stimanja da uvjeti jednakosti budu zadovoljeni je bilo na vjezbama.) Uvrstimo u pocetnu jednadzbu i dobivamo
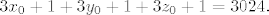
tada je
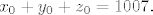
Ova jednakost ima (prema zadatku na vježbama) rješenja 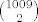 (ovdje i 0 moze biti rjesenje). (ovdje i 0 moze biti rjesenje).
Trazena vjerojatnost je 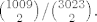
|
|
| [Vrh] |
|
barbarag
Forumaš(ica)

Pridružen/a: 27. 03. 2008. (14:54:10)
Postovi: (29)16
|
|
| [Vrh] |
|
insane_raver
Forumaš(ica)


Pridružen/a: 05. 05. 2009. (21:55:06)
Postovi: (1DB)16
Spol: 
Lokacija: ZGB
|
|
| [Vrh] |
|
Tvrtko
Forumaš(ica)

Pridružen/a: 21. 10. 2006. (12:12:34)
Postovi: (10A)16
Lokacija: CCP 4345 / PMF-MO 225
|
|
| [Vrh] |
|
kakt00s
Forumaš(ica)


Pridružen/a: 17. 10. 2007. (12:19:40)
Postovi: (183)16
Spol: 
Lokacija: :ɐɾıɔɐʞoן
|
|
| [Vrh] |
|
barbarag
Forumaš(ica)

Pridružen/a: 27. 03. 2008. (14:54:10)
Postovi: (29)16
|
|
| [Vrh] |
|
5kyica
Forumaš(ica)

Pridružen/a: 03. 12. 2007. (16:11:37)
Postovi: (16)16
|
|
| [Vrh] |
|
Crvenkapica
Forumaš(ica)

Pridružen/a: 16. 04. 2007. (14:52:45)
Postovi: (AB)16
|
|
| [Vrh] |
|
thomary
Forumaš(ica)

Pridružen/a: 20. 11. 2007. (20:45:28)
Postovi: (87)16
|
|
| [Vrh] |
|
Crvenkapica
Forumaš(ica)

Pridružen/a: 16. 04. 2007. (14:52:45)
Postovi: (AB)16
|
|
| [Vrh] |
|
thomary
Forumaš(ica)

Pridružen/a: 20. 11. 2007. (20:45:28)
Postovi: (87)16
|
|
| [Vrh] |
|
Crvenkapica
Forumaš(ica)

Pridružen/a: 16. 04. 2007. (14:52:45)
Postovi: (AB)16
|
|
| [Vrh] |
|
thomary
Forumaš(ica)

Pridružen/a: 20. 11. 2007. (20:45:28)
Postovi: (87)16
|
|
| [Vrh] |
|
Crvenkapica
Forumaš(ica)

Pridružen/a: 16. 04. 2007. (14:52:45)
Postovi: (AB)16
|
|
| [Vrh] |
|
tammy
Forumaš(ica)

Pridružen/a: 02. 07. 2007. (20:37:10)
Postovi: (197)16
|
|
| [Vrh] |
|
Crvenkapica
Forumaš(ica)

Pridružen/a: 16. 04. 2007. (14:52:45)
Postovi: (AB)16
|
|
| [Vrh] |
|
tammy
Forumaš(ica)

Pridružen/a: 02. 07. 2007. (20:37:10)
Postovi: (197)16
|
|
| [Vrh] |
|
Crvenkapica
Forumaš(ica)

Pridružen/a: 16. 04. 2007. (14:52:45)
Postovi: (AB)16
|
|
| [Vrh] |
|
Tvrtko
Forumaš(ica)

Pridružen/a: 21. 10. 2006. (12:12:34)
Postovi: (10A)16
Lokacija: CCP 4345 / PMF-MO 225
|
 Postano: 21:46 pet, 4. 6. 2010 Naslov: Postano: 21:46 pet, 4. 6. 2010 Naslov: |
    |
|
|
Mozete ocekivati ono sto se radilo :? :
nezavisnost, ponavljanje pokusa
uvjetne vjerojatnosti, Bayesova formula, formula potpune vjerojatnosti
slučajne varijable, distribucija sl. varijabli
ocekivanje, varijanca, sl. vektori, korelacija
aproksimacija normalnom
(Ako sam na vjezbama rekao nesto vise, slobodno me ispravite.)
Moram reci da meni Bronstajn nikad nije pokazao korisnim, u principu vam iz njega treba
tablica vrijednosti normalne distribucije koju mozete preuzeti [url=http://web.math.hr/nastava/uuv/files/norm.pdf]ovdje[/url], mozete imati i list papira s formulama po vlastitom izboru,
kao i kalkulator. 8)
Meni se cini da je prvi kolokvij obicno uvijek tezi jer sadrzi vise kombinatorike, dok je to u drugom manje potrebno. :wink:
Na proslom kolokviju je bilo i nekoliko slucajeva :twisted: gdje su ljudi napisali [latex]\sum_{n=1}^\infty \frac{1}{3^n}=0[/latex], pa molim da se takve stvari znaju! :roll:
Mozete ocekivati ono sto se radilo  : :
nezavisnost, ponavljanje pokusa
uvjetne vjerojatnosti, Bayesova formula, formula potpune vjerojatnosti
slučajne varijable, distribucija sl. varijabli
ocekivanje, varijanca, sl. vektori, korelacija
aproksimacija normalnom
(Ako sam na vjezbama rekao nesto vise, slobodno me ispravite.)
Moram reci da meni Bronstajn nikad nije pokazao korisnim, u principu vam iz njega treba
tablica vrijednosti normalne distribucije koju mozete preuzeti ovdje, mozete imati i list papira s formulama po vlastitom izboru,
kao i kalkulator. 
Meni se cini da je prvi kolokvij obicno uvijek tezi jer sadrzi vise kombinatorike, dok je to u drugom manje potrebno. 
Na proslom kolokviju je bilo i nekoliko slucajeva  gdje su ljudi napisali gdje su ljudi napisali 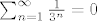 , pa molim da se takve stvari znaju! , pa molim da se takve stvari znaju! 
|
|
| [Vrh] |
|
Crvenkapica
Forumaš(ica)

Pridružen/a: 16. 04. 2007. (14:52:45)
Postovi: (AB)16
|
|
| [Vrh] |
|
|





