| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
zizu
Forumaš(ica)
Pridružen/a: 28. 03. 2010. (18:30:02)
Postovi: (A)16
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
šišmiš
Forumaš(ica)

Pridružen/a: 19. 04. 2010. (21:01:19)
Postovi: (29)16
|
|
| [Vrh] |
|
amimoza
Forumaš(ica)


Pridružen/a: 06. 04. 2010. (12:25:46)
Postovi: (14)16
Spol: 
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 18:38 ned, 6. 6. 2010 Naslov: Postano: 18:38 ned, 6. 6. 2010 Naslov: |
    |
|
|
2.56 (a) Granični kriterij s 1/x. Primjeti da je [latex]\displaystyle \lim_{x \to +\infty} \frac{\ln x}{\sqrt[p]{x}} = 0,\ \forall \, p \geq 1[/latex]
2.56 (b) Uzeti apsolutnu vrijednost, maknuti kosinus. Granični kriterij s [latex]\displaystyle \frac{1}{x^p}[/latex], gdje p može biti bilo što iz [latex]\langle 1, 1.5 \rangle[/latex].
2.57 Integral racionalne funkcije. Jedna primitivna fja. je [latex]\displaystyle \ln \frac{\sqrt{x^2 + 4}}{\sqrt[3]{(3 x + 4)^a}}[/latex]. Dakle, a = 3.
2.59 (b) [latex]\displaystyle \frac{1}{\sqrt{(x - a)(b - x)}} = \frac{1}{\sqrt{\left( \frac{b - a}{2} \right)^2 - \left( x - \frac{a + b}{2} \right)^2}}[/latex] Hint: derivacija od arcsin.
@smajl: supstitucija [latex]t = \sqrt[6]{x}[/latex]
2.56 (a) Granični kriterij s 1/x. Primjeti da je 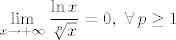
2.56 (b) Uzeti apsolutnu vrijednost, maknuti kosinus. Granični kriterij s 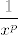 , gdje p može biti bilo što iz , gdje p može biti bilo što iz 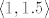 . .
2.57 Integral racionalne funkcije. Jedna primitivna fja. je 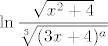 . Dakle, a = 3. . Dakle, a = 3.
2.59 (b) 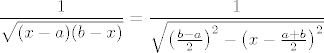 Hint: derivacija od arcsin. Hint: derivacija od arcsin.
@smajl: supstitucija 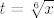
|
|
| [Vrh] |
|
NeonBlack
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (15:46:24)
Postovi: (37)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
NeonBlack
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (15:46:24)
Postovi: (37)16
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 22:03 ned, 6. 6. 2010 Naslov: Postano: 22:03 ned, 6. 6. 2010 Naslov: |
    |
|
|
Ako misliš na drugi kolokvij iz 2008., 2. grupa, zadatak 2. b), onda primjetiš da je lik (čija se površina traži) simetričan s obzirom na x-os, pa traženu površinu možeš izračunati kao (dio površine u I. kvadrantu)*2. Poanta, smiješ baciti korijen i staviti predznak + ispred. :D
Ako misliš na drugi kolokvij iz 2008., 2. grupa, zadatak 2. b), onda primjetiš da je lik (čija se površina traži) simetričan s obzirom na x-os, pa traženu površinu možeš izračunati kao (dio površine u I. kvadrantu)*2. Poanta, smiješ baciti korijen i staviti predznak + ispred. 
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 22:25 ned, 6. 6. 2010 Naslov: Postano: 22:25 ned, 6. 6. 2010 Naslov: |
    |
|
|
Zavisi, npr. u 2. kol. 2008., 1. grupa, 2. b), se može skužiti da je krivulja simetrična s obzirom na x i y os (zbog kvadrata), pa je dovoljno gledati I. kvadrant. Zatim se vidi da je [latex]x \in [-2, 2][/latex], jer je [latex]4 y^2 \geq 0 \ \Leftrightarrow \ 4 x^2 - x^4 \geq 0 \ \Leftrightarrow \ x^2 (x + 2) (x - 2) \leq 0[/latex], pa je tražena površna jednaka [latex]\displaystyle 4 \int \limits_0^2 \sqrt{x^2 - \frac{x^4}{4}} \, dx[/latex].
Zavisi, npr. u 2. kol. 2008., 1. grupa, 2. b), se može skužiti da je krivulja simetrična s obzirom na x i y os (zbog kvadrata), pa je dovoljno gledati I. kvadrant. Zatim se vidi da je 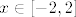 , jer je , jer je 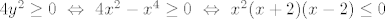 , pa je tražena površna jednaka , pa je tražena površna jednaka 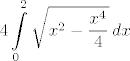 . .
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
A_je_to
Forumaš(ica)

Pridružen/a: 19. 02. 2009. (16:51:22)
Postovi: (6D)16
Spol: 
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
|
















