| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Blondie
Forumaš(ica)


Pridružen/a: 16. 11. 2009. (15:11:18)
Postovi: (47)16
Spol: 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
Neno
Forumaš(ica)

Pridružen/a: 08. 02. 2008. (20:03:15)
Postovi: (98)16
Spol: 
Lokacija: Zagreb
|
 Postano: 0:12 pon, 11. 10. 2010 Naslov: Postano: 0:12 pon, 11. 10. 2010 Naslov: |
    |
|
|
[quote="Blondie"][quote="jirrxj"]
A uputa za 21. zadatak je da povučeš paralelu sa stranicom BC kroz točku A i tamo gdje ona siječe pravac MN označimo točku s npr. slovom R. Sada ako znamo da je PR jednake duljine kao i visina trokuta i da su trokuti MRA i NRA sukladni možemo zbroj PM + PN izraziti preko visine v(na stranicu a).[/quote]
Zašto bi PR bio jednake duljine kao visina trokuta? Piše da je P proizvoljna točka na stranici BC. A da bude jednaka visini, P treba biti točno na polovici BC.[/quote]
Razlog, zašto povlačiš paralelu kroz neku točku je da dobiješ 2 sukladna trokuta, to jest, još [u]moraš [/u]dokazati da su sukladni.
I tako si ovdje kroz A povukla paralelu sa [latex]\overline{BC}[/latex], a sjecište sa [latex]\overline{PN}[/latex] imenovala [latex]R[/latex].
Gledaj skicu: [latex]|PM|+|PN|[/latex] (to je ono što te pita, traži) = [latex]|PM|+[/latex] (sad PN rastaviš na) [latex]|PM|+|MN|=2|PM|+|MN|[/latex]. ( ****zvjezdica, to znači, ovdje ćeš se još vratiti).
1. [latex]|AR|=|AR|[/latex] jer je to zajednička stranica
2. [latex]\angle{NRA}=\angle{MRA}[/latex] pravi kutevi
3. [latex]\angle{NAR}=\angle{ACB}[/latex], kutevi sa paralelnim kracima, [latex]=\angle{ABC}[/latex] (jer je zadan jednakokračni trokut) [latex]=\angle{MAR}[/latex] (kutevi uz transverzalu, uz presječnicu, sa paralelnim kracima).
Sve 3 jednakosti vrijede, ispunjeni su uvjeti teorema SKS, [latex]\triangle{RAN}\cong\triangle{RMA}\implies|NR|=|MR|[/latex].
Vrati se u ****zvjezdicu.
[latex]2|PM+|MN|[/latex] (ne!!!!, prekriži MN, razčlanjuješ MN, umjesto MN pišeš [latex]|MR|+|NR|[/latex]) = [latex]2|PM|+2|MR|[/latex] (jer su jednake MR i NR) [latex]=2(|PM|+|MR|)=2|PR|=2\cdot{v}[/latex] trokuta, koja ne ovisi o izboru, položaju točke [latex]P[/latex].
| Blondie (napisa): | | jirrxj (napisa): |
A uputa za 21. zadatak je da povučeš paralelu sa stranicom BC kroz točku A i tamo gdje ona siječe pravac MN označimo točku s npr. slovom R. Sada ako znamo da je PR jednake duljine kao i visina trokuta i da su trokuti MRA i NRA sukladni možemo zbroj PM + PN izraziti preko visine v(na stranicu a). |
Zašto bi PR bio jednake duljine kao visina trokuta? Piše da je P proizvoljna točka na stranici BC. A da bude jednaka visini, P treba biti točno na polovici BC. |
Razlog, zašto povlačiš paralelu kroz neku točku je da dobiješ 2 sukladna trokuta, to jest, još moraš dokazati da su sukladni.
I tako si ovdje kroz A povukla paralelu sa 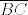 , a sjecište sa , a sjecište sa 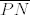 imenovala imenovala 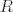 . .
Gledaj skicu:  (to je ono što te pita, traži) = (to je ono što te pita, traži) = 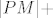 (sad PN rastaviš na) (sad PN rastaviš na) 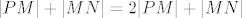 . ( ****zvjezdica, to znači, ovdje ćeš se još vratiti). . ( ****zvjezdica, to znači, ovdje ćeš se još vratiti).
1. 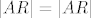 jer je to zajednička stranica jer je to zajednička stranica
2. 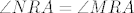 pravi kutevi pravi kutevi
3. 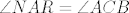 , kutevi sa paralelnim kracima, , kutevi sa paralelnim kracima, 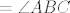 (jer je zadan jednakokračni trokut) (jer je zadan jednakokračni trokut) 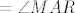 (kutevi uz transverzalu, uz presječnicu, sa paralelnim kracima). (kutevi uz transverzalu, uz presječnicu, sa paralelnim kracima).
Sve 3 jednakosti vrijede, ispunjeni su uvjeti teorema SKS, 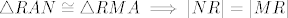 . .
Vrati se u ****zvjezdicu.
 (ne!!!!, prekriži MN, razčlanjuješ MN, umjesto MN pišeš (ne!!!!, prekriži MN, razčlanjuješ MN, umjesto MN pišeš  ) = ) =  (jer su jednake MR i NR) (jer su jednake MR i NR) 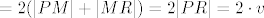 trokuta, koja ne ovisi o izboru, položaju točke trokuta, koja ne ovisi o izboru, položaju točke  . .
|
|
| [Vrh] |
|
jirrxj
Forumaš(ica)

Pridružen/a: 12. 02. 2009. (17:24:06)
Postovi: (40)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
Mignon
Forumaš(ica)


Pridružen/a: 12. 09. 2010. (14:05:45)
Postovi: (B6)16
Spol: 
Lokacija: 206
|
|
| [Vrh] |
|
|









