| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
lalala5
Forumaš(ica)

Pridružen/a: 06. 10. 2010. (17:54:28)
Postovi: (3C)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 23:28 sri, 6. 10. 2010 Naslov: Postano: 23:28 sri, 6. 10. 2010 Naslov: |
    |
|
|
S obzirom da je A skup čije elemente ne znaš, niti nećeš moći raspisati P(A) i F(A).
Kod takvih zadataka, ako nemaš odmah ideju, uvijek je dobro krenuti prvo sa konkretnim skupovima. Razne inkluzije često znaju pasti kada se za A ili B uzme da je prazan skup pa zadaj si da je npr. [latex]A=\emptyset[/latex] i B bilo koji skup različit od praznog, npr. B={1} i provjeri da li relacije štimaju. Ako ne štimaju, nađen je primjer koji neka inkluzija ne zadovoljava, a ako štimaju, onda uzmi za A neki malo kompliciraniji skup, npr. A={1,2}. Nakon malo raspisivanja dobiti ćeš ideju kako na općenitim skupovima funkcioniraju inkluzije.
Npr. za 5.c. Neka je [latex]A\neq\emptyset[/latex] i [latex]B=\emptyset[/latex]. Tada je [latex]\mathcal{P}(A\setminus B)=\mathcal{P}(A\setminus\emptyset)=\mathcal{P}(A)\subseteq\mathcal{P}(A)=\mathcal{P}(A)\setminus\emptyset = \mathcal{P}(A)\setminus\mathcal{P}(\emptyset)=\mathcal{P}(A)\setminus\mathcal{P}(B)[/latex].
Dakle, inkluzija vrijedi ako je B prazan skup. Sada možemo provjeriti što se događa ako B nije prazan, npr. neka je B={1} i neka je A različit od B, npr. A={1,2}.
Tu izračunaj P(A\B), P(A) i P(B) i pogledaj u kakvom su odnosu P(A\B) i P(A)\P(B).
[spoiler]
[latex]\mathcal{P}(A\setminus B)=\mathcal{P}(\{2\})=\{\emptyset, \{2\}\}[/latex].
S druge strane, [latex]\mathcal{P}(A)=\mathcal{P}(\{1,2\})=\{\emptyset, \{1\},\{2\},\{1,2\}\}[/latex]
[latex]\mathcal{P}(B)=\mathcal{P}(\{1\})=\{\emptyset,\{1\}\}[/latex]
pa je [latex]\mathcal{P}(A)\setminus\mathcal{P}(B)=\{\{2\},\{1,2\}\}[/latex] pa inkluzija općenito ne vrijedi.[/spoiler]
S obzirom da je A skup čije elemente ne znaš, niti nećeš moći raspisati P(A) i F(A).
Kod takvih zadataka, ako nemaš odmah ideju, uvijek je dobro krenuti prvo sa konkretnim skupovima. Razne inkluzije često znaju pasti kada se za A ili B uzme da je prazan skup pa zadaj si da je npr. 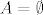 i B bilo koji skup različit od praznog, npr. B={1} i provjeri da li relacije štimaju. Ako ne štimaju, nađen je primjer koji neka inkluzija ne zadovoljava, a ako štimaju, onda uzmi za A neki malo kompliciraniji skup, npr. A={1,2}. Nakon malo raspisivanja dobiti ćeš ideju kako na općenitim skupovima funkcioniraju inkluzije. i B bilo koji skup različit od praznog, npr. B={1} i provjeri da li relacije štimaju. Ako ne štimaju, nađen je primjer koji neka inkluzija ne zadovoljava, a ako štimaju, onda uzmi za A neki malo kompliciraniji skup, npr. A={1,2}. Nakon malo raspisivanja dobiti ćeš ideju kako na općenitim skupovima funkcioniraju inkluzije.
Npr. za 5.c. Neka je 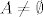 i i 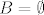 . Tada je . Tada je 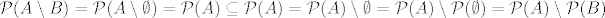 . .
Dakle, inkluzija vrijedi ako je B prazan skup. Sada možemo provjeriti što se događa ako B nije prazan, npr. neka je B={1} i neka je A različit od B, npr. A={1,2}.
Tu izračunaj P(A\B), P(A) i P(B) i pogledaj u kakvom su odnosu P(A\B) i P(A)\P(B).
| Spoiler [hidden; click to show]: |
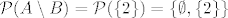 .
S druge strane, 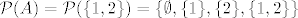
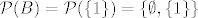
pa je 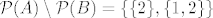 pa inkluzija općenito ne vrijedi. |
_________________
The Dude Abides
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
lalala5
Forumaš(ica)

Pridružen/a: 06. 10. 2010. (17:54:28)
Postovi: (3C)16
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
zbunjena
Forumaš(ica)
Pridružen/a: 28. 06. 2010. (09:50:31)
Postovi: (14)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 18:22 ned, 10. 10. 2010 Naslov: Postano: 18:22 ned, 10. 10. 2010 Naslov: |
    |
|
|
[quote="zbunjena"]može li mi netko detaljnije riješiti 6.zadatak???[/quote]
Treba dokazati [latex](\mathcal{P}(S) \setminus \{ \emptyset \}) \cap (\mathcal{P}(T) \setminus \{ \emptyset \}) = \emptyset \ \Leftrightarrow \ S \cap T = \emptyset[/latex]. Dokažimo ekvivalentnu tvrdnju: [latex](\mathcal{P}(S) \setminus \{ \emptyset \}) \cap (\mathcal{P}(T) \setminus \{ \emptyset \}) \neq \emptyset \ \Leftrightarrow \ S \cap T \neq \emptyset[/latex] (prvotna tvrdnja se može pokazati i preko kontradikcije, ali mi se neda pisati stvari poput "pretpostavimo suprotno" :)).
Dokažimo nužnost. Znači, pretpostavimo da vrijedi [latex](\mathcal{P}(S) \setminus \{ \emptyset \}) \cap (\mathcal{P}(T) \setminus \{ \emptyset \}) \neq \emptyset[/latex]. Slijedi da postoji skup [latex]A \neq \emptyset[/latex] td. [latex]A \in \mathcal{P}(S) \setminus \{ \emptyset \}[/latex] i [latex]A \in \mathcal{P}(T) \setminus \{ \emptyset \}[/latex] (npr. [latex](\mathcal{P}(S) \setminus \{ \emptyset \}) \cap (\mathcal{P}(T) \setminus \{ \emptyset \})[/latex]). To povlači da je [latex]A \subseteq S[/latex] i [latex]A \subseteq T[/latex], tj. [latex]A \subseteq S \cap T[/latex]. Dakle, [latex]S \cap T \neq \emptyset[/latex].
Slično se pokaže dovoljnost, pa to ostavljam tebi. Ako ne ide, javi. :)
| zbunjena (napisa): | | može li mi netko detaljnije riješiti 6.zadatak??? |
Treba dokazati 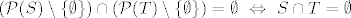 . Dokažimo ekvivalentnu tvrdnju: . Dokažimo ekvivalentnu tvrdnju: 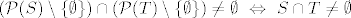 (prvotna tvrdnja se može pokazati i preko kontradikcije, ali mi se neda pisati stvari poput "pretpostavimo suprotno" (prvotna tvrdnja se može pokazati i preko kontradikcije, ali mi se neda pisati stvari poput "pretpostavimo suprotno"  ). ).
Dokažimo nužnost. Znači, pretpostavimo da vrijedi 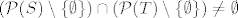 . Slijedi da postoji skup . Slijedi da postoji skup 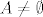 td. td. 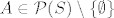 i i 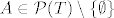 (npr. (npr.  ). To povlači da je ). To povlači da je  i i  , tj. , tj. 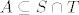 . Dakle, . Dakle, 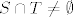 . .
Slično se pokaže dovoljnost, pa to ostavljam tebi. Ako ne ide, javi. 
Zadnja promjena: pmli; 21:47 čet, 28. 10. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 18:22 ned, 10. 10. 2010 Naslov: Postano: 18:22 ned, 10. 10. 2010 Naslov: |
    |
|
|
[quote="zbunjena"]može li mi netko detaljnije riješiti 6.zadatak???
hvala[/quote]
Poanta rješavanja zadataka na forumu je da ti se objasni što nije jasno, a ne da forum bude servis za rješavanje zadataka. :wink:
Dakle, prvi korak bi bio da napišeš svoj pokušaj rješavanja i objasniš gdje si zapela i što ti nije jasno.
Kratki hintovi: s obzirom da se u rečenici pojavljuje ako i samo ako, treba se dokazati
1) [latex]P(S)\setminus\{\emptyset\}[/latex] i [latex]P(T)\setminus\{\emptyset\}[/latex] disjunktni -> S i T disjunktni
2) S i T disjunktni -> [latex]P(S)\setminus\{\emptyset\}[/latex] i [latex]P(T)\setminus\{\emptyset\}[/latex] disjunktni
1) Koja je definicija partitivnog skupa? Da li partitivni skup skupa S sadrži skup S? Ako su čitavi [latex]P(S)\setminus\{\emptyset\}[/latex] i [latex]P(T)\setminus\{\emptyset\}[/latex] disjunktni , a S i T su sadržani u pripadnim partitivnim skupovima, što to onda govori o S i T?
2) Ako su S i T disjunktni, može li se dogoditi da postoji takav podskup od S (odnosno T) koji nije prazan, a da sadrži neki element koji je iz T (odnosno S)?
| zbunjena (napisa): | može li mi netko detaljnije riješiti 6.zadatak???
hvala |
Poanta rješavanja zadataka na forumu je da ti se objasni što nije jasno, a ne da forum bude servis za rješavanje zadataka. 
Dakle, prvi korak bi bio da napišeš svoj pokušaj rješavanja i objasniš gdje si zapela i što ti nije jasno.
Kratki hintovi: s obzirom da se u rečenici pojavljuje ako i samo ako, treba se dokazati
1) 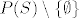 i i 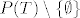 disjunktni → S i T disjunktni disjunktni → S i T disjunktni
2) S i T disjunktni → 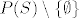 i i 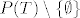 disjunktni disjunktni
1) Koja je definicija partitivnog skupa? Da li partitivni skup skupa S sadrži skup S? Ako su čitavi 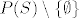 i i 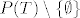 disjunktni , a S i T su sadržani u pripadnim partitivnim skupovima, što to onda govori o S i T? disjunktni , a S i T su sadržani u pripadnim partitivnim skupovima, što to onda govori o S i T?
2) Ako su S i T disjunktni, može li se dogoditi da postoji takav podskup od S (odnosno T) koji nije prazan, a da sadrži neki element koji je iz T (odnosno S)?
_________________
The Dude Abides
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
|
| [Vrh] |
|
zbunjena
Forumaš(ica)
Pridružen/a: 28. 06. 2010. (09:50:31)
Postovi: (14)16
Spol: 
|
|
| [Vrh] |
|
Rufert
Forumaš(ica)

Pridružen/a: 02. 10. 2010. (17:58:52)
Postovi: (12)16
Spol: 
Lokacija: Dubrava
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
Rufert
Forumaš(ica)

Pridružen/a: 02. 10. 2010. (17:58:52)
Postovi: (12)16
Spol: 
Lokacija: Dubrava
|
|
| [Vrh] |
|
|

















