| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Fikus
Forumaš(ica)


Pridružen/a: 14. 07. 2010. (00:00:23)
Postovi: (1C)16
Lokacija: Somewhere around the world
|
 Postano: 17:19 pet, 22. 10. 2010 Naslov: Inverz funkcije na intervalu Postano: 17:19 pet, 22. 10. 2010 Naslov: Inverz funkcije na intervalu |
    |
|
|
ovako, zanima me dali ja kod 4. zadatka kad trazim inverz funkcije na nekom intervalu trebam sve raspisivat ko sto se radilo na vjezbama, tipa f|<0,1>:<0,1>-->R (restrigirano jel), pa onda tako rjesavat, il mogu jednostavno napisat x^2+2x=y i rijesit sve po x, i onda kasnije samo uvrstit u kompoziciju...
Mislim malo glupo pitanje, al neda mi se cijelo vrijeme tak raspisivat, kad za duplo krace vremena mogu naci inverz, pa me zanima jel se to mora bas tak, oce se gubit bodovi ako se ne ide tako postepeno, jer mislim ako dokazemo prije u zadatku da su sve kompozicije injekcije onda mi nema smisla sve to pisat i raspisivat kad mugu jednostavno napisat f(x)=y i rijesit sve po x, nadam se da ste shvatili sta pitam:D hvala unaprijed
ovako, zanima me dali ja kod 4. zadatka kad trazim inverz funkcije na nekom intervalu trebam sve raspisivat ko sto se radilo na vjezbama, tipa f|<0,1>:<0,1>-->R (restrigirano jel), pa onda tako rjesavat, il mogu jednostavno napisat x^2+2x=y i rijesit sve po x, i onda kasnije samo uvrstit u kompoziciju...
Mislim malo glupo pitanje, al neda mi se cijelo vrijeme tak raspisivat, kad za duplo krace vremena mogu naci inverz, pa me zanima jel se to mora bas tak, oce se gubit bodovi ako se ne ide tako postepeno, jer mislim ako dokazemo prije u zadatku da su sve kompozicije injekcije onda mi nema smisla sve to pisat i raspisivat kad mugu jednostavno napisat f(x)=y i rijesit sve po x, nadam se da ste shvatili sta pitam:D hvala unaprijed
_________________
Pokušate li, možda nećete uspjeti, ne pokušate li, sigurno nećete.
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
Fikus
Forumaš(ica)


Pridružen/a: 14. 07. 2010. (00:00:23)
Postovi: (1C)16
Lokacija: Somewhere around the world
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 9:20 ned, 24. 10. 2010 Naslov: Postano: 9:20 ned, 24. 10. 2010 Naslov: |
    |
|
|
Da, možeš to i tako shvatiti (pri čemu to zapravo nije restrikcija funkcije u doslovnom smislu tog izraza). Mislim, ako se [latex]\[-2,0\rangle[/latex] nikad ne postiže, praslika tog intervala je [latex]\emptyset[/latex]. Znaš da vrijedi [latex]f^{-1}(\[-2,8\])=f^{-1}(\[-2,0\rangle\cup\[0,8\])[/latex], a koristeći da je praslika unije ujedno i unija praslika, dobivaš da je to jednako [latex]f^{-1}(\[-2,0\rangle)\cup f^{-1}(\[0,8\])=\emptyset\cup f^{-1}(\[0,8\])=f^{-1}(\[0,8\])[/latex].
Da, možeš to i tako shvatiti (pri čemu to zapravo nije restrikcija funkcije u doslovnom smislu tog izraza). Mislim, ako se 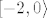 nikad ne postiže, praslika tog intervala je nikad ne postiže, praslika tog intervala je  . Znaš da vrijedi . Znaš da vrijedi 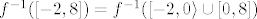 , a koristeći da je praslika unije ujedno i unija praslika, dobivaš da je to jednako , a koristeći da je praslika unije ujedno i unija praslika, dobivaš da je to jednako 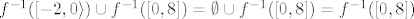 . .
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 10:36 ned, 24. 10. 2010 Naslov: Postano: 10:36 ned, 24. 10. 2010 Naslov: |
    |
|
|
Možeš ako ti je tako lakše, to je svakako točno. Samo, nemoj se opterećivati traženjem slike, pa onda gledanjem jel praslika podskup od slike ili je nekakva ovakva situacija itd. Prirodno ćeš sve ovo moći pročitati s grafa ili kako već rješavaš zadatak - npr. neka je [latex]f(x)=\sin^2 x[/latex] i neka se traži [latex]f^{-1}(\[-1,2\])[/latex]. Sad, ti ne moraš uvidjeti da je zapravo slika funkcije [latex]f[/latex] jednaka [latex]\[0,1\][/latex] (makar vjerojatno hoćeš, ali recimo diskusije radi da to nisi primijetio), pa da onda primjenjuješ ove unije.
Pogledaj kako bismo riješili taj zadatak s kompozicijom: [latex]g(x)=x^2[/latex], [latex]h(x)=\sin h[/latex] i [latex]f=g\circ h[/latex]. Dakle, tražimo [latex]f^{-1}(\[-1,2\])[/latex], tj. [latex]h^{-1}(g^{-1}(\[-1,2\]))[/latex]. E, sad pogledaj prvo kada je [latex]g[/latex] od [latex]-1[/latex] do [latex]2[/latex]. To pogledaj s grafa ili računski ili što već: rješenje je [latex]\[-\sqrt{2},\sqrt{2}\][/latex]. Sad, mi primjećujemo da [latex]g[/latex] uopće nikad nije manji od [latex]0[/latex], ali to nam nije od nekog interesa. Na kraju, zanima nas [latex]h^{-1}(\[-\sqrt{2},\sqrt{2}\])[/latex]. Dakle, kada je sinus unutar tog intervala. No, to je, naravno, uvijek: sinus ide od [latex]-1[/latex] do [latex]1[/latex]. Dakle, ukupno rješenje je cijeli [latex]\mathbb{R}[/latex]. što smo legalno dobili bez da smo igdje eksplicitno tražili sliku ove funkcije.
Naravno, ovaj zadatak se mogao trivijalno odmah i direktno riješiti, ali to nije bila poanta. :D
Možeš ako ti je tako lakše, to je svakako točno. Samo, nemoj se opterećivati traženjem slike, pa onda gledanjem jel praslika podskup od slike ili je nekakva ovakva situacija itd. Prirodno ćeš sve ovo moći pročitati s grafa ili kako već rješavaš zadatak - npr. neka je 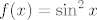 i neka se traži i neka se traži 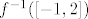 . Sad, ti ne moraš uvidjeti da je zapravo slika funkcije . Sad, ti ne moraš uvidjeti da je zapravo slika funkcije  jednaka jednaka 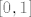 (makar vjerojatno hoćeš, ali recimo diskusije radi da to nisi primijetio), pa da onda primjenjuješ ove unije. (makar vjerojatno hoćeš, ali recimo diskusije radi da to nisi primijetio), pa da onda primjenjuješ ove unije.
Pogledaj kako bismo riješili taj zadatak s kompozicijom:  , , 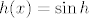 i i 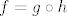 . Dakle, tražimo . Dakle, tražimo 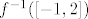 , tj. , tj. 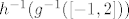 . E, sad pogledaj prvo kada je . E, sad pogledaj prvo kada je  od od  do do  . To pogledaj s grafa ili računski ili što već: rješenje je . To pogledaj s grafa ili računski ili što već: rješenje je 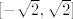 . Sad, mi primjećujemo da . Sad, mi primjećujemo da  uopće nikad nije manji od uopće nikad nije manji od  , ali to nam nije od nekog interesa. Na kraju, zanima nas , ali to nam nije od nekog interesa. Na kraju, zanima nas 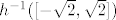 . Dakle, kada je sinus unutar tog intervala. No, to je, naravno, uvijek: sinus ide od . Dakle, kada je sinus unutar tog intervala. No, to je, naravno, uvijek: sinus ide od  do do  . Dakle, ukupno rješenje je cijeli . Dakle, ukupno rješenje je cijeli  . što smo legalno dobili bez da smo igdje eksplicitno tražili sliku ove funkcije. . što smo legalno dobili bez da smo igdje eksplicitno tražili sliku ove funkcije.
Naravno, ovaj zadatak se mogao trivijalno odmah i direktno riješiti, ali to nije bila poanta. 
|
|
| [Vrh] |
|
|







