| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
 Postano: 20:06 sub, 23. 10. 2010 Naslov: Postano: 20:06 sub, 23. 10. 2010 Naslov: |
    |
|
|
Kad bi funkcija bila surjekcija onda bi postojao x1 takav da je [latex]f(x1)=100->99=sin^3(x1)[/latex], što je nemoguće.
Što se tiče injekcije, raspisi po samoj definiciji iste.[latex] f(x1)=f(x2) -> x1=x2[/latex],tj.[latex]sin^3(x1) +1=sin^3(x2) +1 -> sin^3(x1) -sin^3(x2)=0 [/latex] i sad koristis formulu za razliku kubova pa imas:
[latex](sin(x1) - sin(x2))(sin^2(x1) +sin(x1)sin(x2) + sin^2(x2)=0[/latex]
Slucaj a) sin(x1)=sin(x2) . Sad nisam siguran je li potrebno dokazivati da je sin(x) injekcija na ovom intervalu. Ugl je, pa to povlaci x1=x2.
Slucaj b) posto su sin(x1) i sin (x2) oboje negativni za svaki x1,x2 u domeni, onda je njihov produkt pozitivan, pa je i 2sin(x1)sin(x2)>sin(x1)sin(x2). Takodjer je sin^2(x1) + sin^2(x2)>=2sin(x1)sin(x2) po A-G nejednakosti, a jednakost se postize kad su oba jednaki. Znaci izraz u drugoj zagradi moze biti 0 ako i samo ako su x1=x2=2PI.
Ovo se takodjer moze rijesiti nadopunom do potpunog kvadrata..
Sto se tice inverza, mozes gledati ovako: f(x) postize vrijednosti u intervalu [0,1], pa f(x)-1 postize vrijednosti od [-1,0], pa (f(x)-1)^(1/3) postize vrijednosti u intervalu [-1,0]. Znaci da mozes izraziti x jer je arcsin(p) definirana za sve p koji su u intervalu [-1,1].
Kad bi funkcija bila surjekcija onda bi postojao x1 takav da je 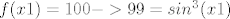 , što je nemoguće. , što je nemoguće.
Što se tiče injekcije, raspisi po samoj definiciji iste.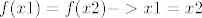 ,tj. ,tj.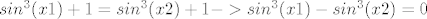 i sad koristis formulu za razliku kubova pa imas: i sad koristis formulu za razliku kubova pa imas:
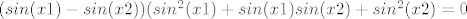
Slucaj a) sin(x1)=sin(x2) . Sad nisam siguran je li potrebno dokazivati da je sin(x) injekcija na ovom intervalu. Ugl je, pa to povlaci x1=x2.
Slucaj b) posto su sin(x1) i sin (x2) oboje negativni za svaki x1,x2 u domeni, onda je njihov produkt pozitivan, pa je i 2sin(x1)sin(x2)>sin(x1)sin(x2). Takodjer je sin^2(x1) + sin^2(x2)>=2sin(x1)sin(x2) po A-G nejednakosti, a jednakost se postize kad su oba jednaki. Znaci izraz u drugoj zagradi moze biti 0 ako i samo ako su x1=x2=2PI.
Ovo se takodjer moze rijesiti nadopunom do potpunog kvadrata..
Sto se tice inverza, mozes gledati ovako: f(x) postize vrijednosti u intervalu [0,1], pa f(x)-1 postize vrijednosti od [-1,0], pa (f(x)-1)^(1/3) postize vrijednosti u intervalu [-1,0]. Znaci da mozes izraziti x jer je arcsin(p) definirana za sve p koji su u intervalu [-1,1].
|
|
| [Vrh] |
|
rimidalv1991
Forumaš(ica)

Pridružen/a: 07. 07. 2009. (21:14:20)
Postovi: (22)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
rimidalv1991
Forumaš(ica)

Pridružen/a: 07. 07. 2009. (21:14:20)
Postovi: (22)16
|
|
| [Vrh] |
|
sailor m
Forumaš(ica)
Pridružen/a: 23. 10. 2010. (10:46:13)
Postovi: (4E)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 15:09 ned, 24. 10. 2010 Naslov: Postano: 15:09 ned, 24. 10. 2010 Naslov: |
    |
|
|
[quote="sailor m"]da li na kolokviju baš moram dokazivat formulama da li je surjekcija (ili injekcija) ili mogu nacrtat graf i pomoći njega pokazati da li je ili nije?[/quote]
Što se surjektivnosti tiče, dovoljno je odrediti sliku, imajući na umu da je svaka fja surjekcija na svoju sliku (i napisati to, ako osjećaš potrebu :)). Za injektivnost treba reći da je nešto strogo rastuće/padajuće. Strogu monotonost ne treba dokazivati, jer ste za jednostavnije fje. odredili kako se ponašaju na predavanjima/vježbama, pa se na to slobodno pozivate.
Npr. pojavi ti se negdje fja. [latex]x \mapsto x^2[/latex]. Možeš bez grižnje savjesti reći da je to bijekcija sa [latex][0, +\infty \rangle[/latex] na to isto. :)
[quote="Tomislav"]Koliko ja znam, citanje iz grafa nikad se nije smatralo dokazom..[/quote]
Istina, ali za sada se ne očekuje od vas da znate dokazati, npr. da je [latex]f : \mathbb{R} \to [0, +\infty \rangle[/latex], [latex]f(x) = x^2[/latex] surjekcija. :)
| sailor m (napisa): | | da li na kolokviju baš moram dokazivat formulama da li je surjekcija (ili injekcija) ili mogu nacrtat graf i pomoći njega pokazati da li je ili nije? |
Što se surjektivnosti tiče, dovoljno je odrediti sliku, imajući na umu da je svaka fja surjekcija na svoju sliku (i napisati to, ako osjećaš potrebu  ). Za injektivnost treba reći da je nešto strogo rastuće/padajuće. Strogu monotonost ne treba dokazivati, jer ste za jednostavnije fje. odredili kako se ponašaju na predavanjima/vježbama, pa se na to slobodno pozivate. ). Za injektivnost treba reći da je nešto strogo rastuće/padajuće. Strogu monotonost ne treba dokazivati, jer ste za jednostavnije fje. odredili kako se ponašaju na predavanjima/vježbama, pa se na to slobodno pozivate.
Npr. pojavi ti se negdje fja. 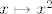 . Možeš bez grižnje savjesti reći da je to bijekcija sa . Možeš bez grižnje savjesti reći da je to bijekcija sa 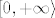 na to isto. na to isto. 
| Tomislav (napisa): | | Koliko ja znam, citanje iz grafa nikad se nije smatralo dokazom.. |
Istina, ali za sada se ne očekuje od vas da znate dokazati, npr. da je 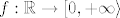 , , 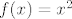 surjekcija. surjekcija. 
|
|
| [Vrh] |
|
sailor m
Forumaš(ica)
Pridružen/a: 23. 10. 2010. (10:46:13)
Postovi: (4E)16
|
|
| [Vrh] |
|
|








