| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 18:42 sub, 9. 10. 2010 Naslov: Postano: 18:42 sub, 9. 10. 2010 Naslov: |
    |
|
|
Ja mislim, ali samo mislim, da nebi trebali biti takvi zadaci za 15 min, ma da opet, koliko kazu, zadaci iz zadace ce biti u blicu (kao), a ako izlucimo bar zadanja 3 zadatka onda od skupova ostaje samo 5.zad, sto je sad malo cudno.
Da se uvjerim, pisemo samo skupove bez relacija, jel tako ?
Ja mislim, ali samo mislim, da nebi trebali biti takvi zadaci za 15 min, ma da opet, koliko kazu, zadaci iz zadace ce biti u blicu (kao), a ako izlucimo bar zadanja 3 zadatka onda od skupova ostaje samo 5.zad, sto je sad malo cudno.
Da se uvjerim, pisemo samo skupove bez relacija, jel tako ?
|
|
| [Vrh] |
|
27re
Forumaš(ica)


Pridružen/a: 06. 10. 2010. (16:07:02)
Postovi: (17)16
|
 Postano: 21:32 sub, 9. 10. 2010 Naslov: Postano: 21:32 sub, 9. 10. 2010 Naslov: |
    |
|
|
[quote="frutabella"]Ja mislim, ali samo mislim, da nebi trebali biti takvi zadaci za 15 min, ma da opet, koliko kazu, zadaci iz zadace ce biti u blicu (kao), a ako izlucimo bar zadanja 3 zadatka onda od skupova ostaje samo 5.zad, sto je sad malo cudno.
Da se uvjerim, pisemo samo skupove bez relacija, jel tako ?[/quote]
Pa kao prvo relacije nisu bile u ovoj zadaći, a i rečeno je da ih neće biti
| frutabella (napisa): | Ja mislim, ali samo mislim, da nebi trebali biti takvi zadaci za 15 min, ma da opet, koliko kazu, zadaci iz zadace ce biti u blicu (kao), a ako izlucimo bar zadanja 3 zadatka onda od skupova ostaje samo 5.zad, sto je sad malo cudno.
Da se uvjerim, pisemo samo skupove bez relacija, jel tako ? |
Pa kao prvo relacije nisu bile u ovoj zadaći, a i rečeno je da ih neće biti
|
|
| [Vrh] |
|
888
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (18:26:14)
Postovi: (29)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 13:00 ned, 10. 10. 2010 Naslov: Postano: 13:00 ned, 10. 10. 2010 Naslov: |
    |
|
|
Pa trebala bi se dokazati opcenita tvrdnja...
u a) dijelu, to znaci da treba raspisati opcenito, a u b) zadatku (ako se nasluti da tvrdnja ne vrijedi), dovoljno je naci konkretan kontraprimjer:
X={1,2} F={{1},{2}}
Y={2,3}, G={{2},{3}}
Sada imamo FuG={{1},{2},{3}}, a to je ocito particija skupa {1,2,3}=XuY,
ali X i Y nisu disjunktni. =>b) ne vrijedi.
Ako treba jos raspisati a), reci
Pa trebala bi se dokazati opcenita tvrdnja...
u a) dijelu, to znaci da treba raspisati opcenito, a u b) zadatku (ako se nasluti da tvrdnja ne vrijedi), dovoljno je naci konkretan kontraprimjer:
X={1,2} F={{1},{2}}
Y={2,3}, G={{2},{3}}
Sada imamo FuG={{1},{2},{3}}, a to je ocito particija skupa {1,2,3}=XuY,
ali X i Y nisu disjunktni. =>b) ne vrijedi.
Ako treba jos raspisati a), reci
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 14:29 ned, 10. 10. 2010 Naslov: Postano: 14:29 ned, 10. 10. 2010 Naslov: |
    |
|
|
[quote="pbakic"]Pa trebala bi se dokazati opcenita tvrdnja...
u a) dijelu, to znaci da treba raspisati opcenito, a u b) zadatku (ako se nasluti da tvrdnja ne vrijedi), dovoljno je naci konkretan kontraprimjer:
X={1,2} F={{1},{2}}
Y={2,3}, G={{2},{3}}
Sada imamo FuG={{1},{2},{3}}, a to je ocito particija skupa {1,2,3}=XuY,
ali X i Y nisu disjunktni. =>b) ne vrijedi.
Ako treba jos raspisati a), reci[/quote]
Ako može za mene raspisati a) još... Intuitivno mi je jasno zašto je tako, ali ne znam da li mogu to ispravno formalno dokazati.
| pbakic (napisa): | Pa trebala bi se dokazati opcenita tvrdnja...
u a) dijelu, to znaci da treba raspisati opcenito, a u b) zadatku (ako se nasluti da tvrdnja ne vrijedi), dovoljno je naci konkretan kontraprimjer:
X={1,2} F={{1},{2}}
Y={2,3}, G={{2},{3}}
Sada imamo FuG={{1},{2},{3}}, a to je ocito particija skupa {1,2,3}=XuY,
ali X i Y nisu disjunktni. ⇒b) ne vrijedi.
Ako treba jos raspisati a), reci |
Ako može za mene raspisati a) još... Intuitivno mi je jasno zašto je tako, ali ne znam da li mogu to ispravno formalno dokazati.
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 14:44 ned, 10. 10. 2010 Naslov: Postano: 14:44 ned, 10. 10. 2010 Naslov: |
    |
|
|
evo za a) dokaz:
Da bi FuG bila particija XuY, mora zadovoljavati ona 3 svojstva:
1) FuG ne sadrzi prazan skup (to je ocito, jer ni F ni G ne sadrze prazan skup, buduci da su F i G particije)
2) za svaka dva elementa iz FuG, presjek im je prazan:
ako su oba elementa iz F ili oba iz G, onda im je presjek prazan jer su F i G particije pa to svojstvo vrijedi unutar njih.
ako je jedan iz F, drugi iz G: buduci da su X i Y disjunktni, onda pogotovo za bilo koja dva podskupa [latex]A\subseteq X[/latex] i [latex]B\subseteq Y[/latex] vrijedi [latex]A\cap B=\varnothing[/latex].
3) unija svih elemenata FuG daje XuY:
Unija svih elemenata iz F daje X (jer je F particija), unija svih elemenata iz G daje Y, pa kad napravimo uniju jednih i drugih, dobit cemo XuY
evo za a) dokaz:
Da bi FuG bila particija XuY, mora zadovoljavati ona 3 svojstva:
1) FuG ne sadrzi prazan skup (to je ocito, jer ni F ni G ne sadrze prazan skup, buduci da su F i G particije)
2) za svaka dva elementa iz FuG, presjek im je prazan:
ako su oba elementa iz F ili oba iz G, onda im je presjek prazan jer su F i G particije pa to svojstvo vrijedi unutar njih.
ako je jedan iz F, drugi iz G: buduci da su X i Y disjunktni, onda pogotovo za bilo koja dva podskupa 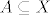 i i 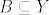 vrijedi vrijedi 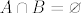 . .
3) unija svih elemenata FuG daje XuY:
Unija svih elemenata iz F daje X (jer je F particija), unija svih elemenata iz G daje Y, pa kad napravimo uniju jednih i drugih, dobit cemo XuY
Zadnja promjena: pbakic; 19:28 ned, 10. 10. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
AnaP
Forumaš(ica)

Pridružen/a: 02. 05. 2008. (15:41:46)
Postovi: (153)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
AnaP
Forumaš(ica)

Pridružen/a: 02. 05. 2008. (15:41:46)
Postovi: (153)16
|
|
| [Vrh] |
|
<gogo>
Forumaš(ica)


Pridružen/a: 09. 09. 2010. (09:09:31)
Postovi: (19)16
Spol: 
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
888
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (18:26:14)
Postovi: (29)16
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
 Postano: 21:17 pon, 25. 10. 2010 Naslov: Postano: 21:17 pon, 25. 10. 2010 Naslov: |
    |
|
|
zna li itko,3, zadatak iz druge domaće zadaće...tj zanima me samo,je li ta relacija totalni uređaj na RxR? i ako je,molila bih da netko obajsni zašto...
http://web.math.hr/nastava/em/EM1/zadace/dz2010/dz2.pdf --> tu je taj zadatak,3.
hvala unaprijed =)
zna li itko,3, zadatak iz druge domaće zadaće...tj zanima me samo,je li ta relacija totalni uređaj na RxR? i ako je,molila bih da netko obajsni zašto...
http://web.math.hr/nastava/em/EM1/zadace/dz2010/dz2.pdf --> tu je taj zadatak,3.
hvala unaprijed =)
|
|
| [Vrh] |
|
<gogo>
Forumaš(ica)


Pridružen/a: 09. 09. 2010. (09:09:31)
Postovi: (19)16
Spol: 
|
|
| [Vrh] |
|
|














