| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Allmighty
Forumaš(ica)

Pridružen/a: 09. 07. 2009. (12:59:46)
Postovi: (22)16
|
|
| [Vrh] |
|
some_dude
Forumaš(ica)
Pridružen/a: 08. 11. 2009. (16:23:13)
Postovi: (59)16
Spol: 
Lokacija: Zd-Zg
|
|
| [Vrh] |
|
Pero Kvrzica
Forumaš(ica)
Pridružen/a: 26. 06. 2010. (12:45:56)
Postovi: (19)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
homesweethome
Forumaš(ica)

Pridružen/a: 21. 10. 2009. (16:25:25)
Postovi: (1C)16
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
ankovacic
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (19:28:17)
Postovi: (5C)16
Spol: 
|
 Postano: 16:08 ned, 31. 10. 2010 Naslov: Postano: 16:08 ned, 31. 10. 2010 Naslov: |
    |
|
|
http://web.math.hr/nastava/uuv/files/chap1.pdf
Zadatak 1.17. Koji je prostor elementarnih događaja uopće i koji mu je kardinalni broj?
Ja mislim da je nešto tipa ovog ali sam duboko nesiguran u to:
O={(a1,..ai,6..,6): a1,...ai€{1,...5}} X {(b1,..bj,6..,6): b1,...bj€{1,...6}} X {(c1,..ck..,6): c1,...ck€{1,...6}} i da je k(O)=5^(i+j+k)
MOLIM POMOĆ
http://web.math.hr/nastava/uuv/files/chap1.pdf
Zadatak 1.17. Koji je prostor elementarnih događaja uopće i koji mu je kardinalni broj?
Ja mislim da je nešto tipa ovog ali sam duboko nesiguran u to:
O={(a1,..ai,6..,6): a1,...ai€{1,...5}} X {(b1,..bj,6..,6): b1,...bj€{1,...6}} X {(c1,..ck..,6): c1,...ck€{1,...6}} i da je k(O)=5^(i+j+k)
MOLIM POMOĆ
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
homesweethome
Forumaš(ica)

Pridružen/a: 21. 10. 2009. (16:25:25)
Postovi: (1C)16
|
|
| [Vrh] |
|
NeonBlack
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (15:46:24)
Postovi: (37)16
|
|
| [Vrh] |
|
some_dude
Forumaš(ica)
Pridružen/a: 08. 11. 2009. (16:23:13)
Postovi: (59)16
Spol: 
Lokacija: Zd-Zg
|
|
| [Vrh] |
|
NeonBlack
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (15:46:24)
Postovi: (37)16
|
 Postano: 18:43 pon, 1. 11. 2010 Naslov: Postano: 18:43 pon, 1. 11. 2010 Naslov: |
    |
|
|
Hvala! Bio mi je problem šta sam ga pokušavala riješit kako nam ga je ona na satu započela, tako da još ne znam di sam se pogubila :D
Eee, i još nešto, al` nije P(h1)=P(h2)= 1/2^3 :? . Mislim, ne utječe na rezultat jer se skrati,ali samo za provjeru sebe pitam.
Hvala! Bio mi je problem šta sam ga pokušavala riješit kako nam ga je ona na satu započela, tako da još ne znam di sam se pogubila 
Eee, i još nešto, al` nije P(h1)=P(h2)= 1/2^3  . Mislim, ne utječe na rezultat jer se skrati,ali samo za provjeru sebe pitam. . Mislim, ne utječe na rezultat jer se skrati,ali samo za provjeru sebe pitam.
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 17:44 uto, 2. 11. 2010 Naslov: Postano: 17:44 uto, 2. 11. 2010 Naslov: |
    |
|
|
Tu nam treba formula potpune vjerojatnosti:
neka su
H1={izabrali smo prvi dio kutije} , P(H1)=1/2
H2={izabrali smo drugi dio kutije} , P(H2)=1/2
i neka je dogadjaj A={izvukli smo dvije istobojne kuglice}
Tada je P(A)=P(A|H1)P(H1) + P(A|H2)P(H2) (*)
preostaje, dakle, izracunati P(A|H1) i P(A|H2)
P(A|H1):
nalazimo se u prvom dijelu kutije, imamo 3 plave i 3 bijele kuglice na raspolaganju
Dvije istobojne mozemo izabrati na [latex]2{3 \choose 2}
[/latex] - dvojka za odabir boje i 3 povrh 2 za odabir 2 od 3 kuglice
Ukupno mozemo izabrati par kuglica na [latex]{6 \choose 2}[/latex] nacina.
=> [latex]P(A|H1)=\frac{2{3 \choose 2}}{{6 \choose 2}} = \frac{2}{5}[/latex]
P(A|H2):
slicno kao u prvom slucaju, samo sada imamo
[latex]{3 \choose 2}+{4 \choose 2} [/latex] povoljnih odabira, a [latex]{7 \choose 2}[/latex] mogucih
=> [latex]P(A|H2)=\frac{{3 \choose 2}+{4 \choose 2}}{{7 \choose 2}}[/latex]
Sad se ovi rezultati vrate u (*), i to je to...
Tu nam treba formula potpune vjerojatnosti:
neka su
H1={izabrali smo prvi dio kutije} , P(H1)=1/2
H2={izabrali smo drugi dio kutije} , P(H2)=1/2
i neka je dogadjaj A={izvukli smo dvije istobojne kuglice}
Tada je P(A)=P(A|H1)P(H1) + P(A|H2)P(H2) (*)
preostaje, dakle, izracunati P(A|H1) i P(A|H2)
P(A|H1):
nalazimo se u prvom dijelu kutije, imamo 3 plave i 3 bijele kuglice na raspolaganju
Dvije istobojne mozemo izabrati na 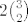 - dvojka za odabir boje i 3 povrh 2 za odabir 2 od 3 kuglice - dvojka za odabir boje i 3 povrh 2 za odabir 2 od 3 kuglice
Ukupno mozemo izabrati par kuglica na 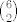 nacina. nacina.
⇒ 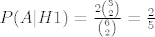
P(A|H2):
slicno kao u prvom slucaju, samo sada imamo
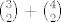 povoljnih odabira, a povoljnih odabira, a 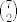 mogucih mogucih
⇒ 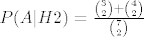
Sad se ovi rezultati vrate u (*), i to je to...
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Allmighty
Forumaš(ica)

Pridružen/a: 09. 07. 2009. (12:59:46)
Postovi: (22)16
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 23:24 uto, 2. 11. 2010 Naslov: Postano: 23:24 uto, 2. 11. 2010 Naslov: |
    |
|
|
Uzmimo, radi kraćeg zapisa, da se radi o brojevima, a ne o bojama (znači, kuglice nisu obojane, nego su na njima zapisani brojevi od 1 do 5).
Označimo s [latex]A_i[/latex] događaj "u 10 izvlačenja nikad se nije dogodio ishod [latex](i, i)[/latex]". Vidimo da je [latex]\displaystyle \mathsf{P}(A_i) = \left( \frac{25 - 1}{25} \right)^{10}[/latex], [latex]\displaystyle \mathsf{P}(A_i \cap A_j) = \left( \frac{25 - 2}{25} \right)^{10}[/latex] za [latex]i \neq j[/latex], itd.
Nas zanima [latex]\displaystyle \mathsf{P} \left( \bigcap_{i = 1}^5 A_i^{\complement} \right) = 1 - \mathsf{P} \left( \bigcup_{i = 1}^5 A_i \right)[/latex], što možemo raspisati po Sylvestru. Dobi se [latex]\frac{1406527416}{762939453125} \approx 0.00184356[/latex].
Uzmimo, radi kraćeg zapisa, da se radi o brojevima, a ne o bojama (znači, kuglice nisu obojane, nego su na njima zapisani brojevi od 1 do 5).
Označimo s 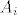 događaj "u 10 izvlačenja nikad se nije dogodio ishod događaj "u 10 izvlačenja nikad se nije dogodio ishod 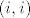 ". Vidimo da je ". Vidimo da je 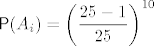 , , 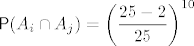 za za 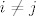 , itd. , itd.
Nas zanima 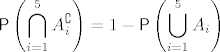 , što možemo raspisati po Sylvestru. Dobi se , što možemo raspisati po Sylvestru. Dobi se 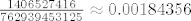 . .
|
|
| [Vrh] |
|
Black Mamba
Forumaš(ica)

Pridružen/a: 12. 10. 2009. (21:08:31)
Postovi: (58)16
|
|
| [Vrh] |
|
|













