| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
spot137
Forumaš(ica)
Pridružen/a: 02. 11. 2009. (13:33:18)
Postovi: (55)16
Spol: 
|
|
| [Vrh] |
|
some_dude
Forumaš(ica)
Pridružen/a: 08. 11. 2009. (16:23:13)
Postovi: (59)16
Spol: 
Lokacija: Zd-Zg
|
 Postano: 15:54 sri, 3. 11. 2010 Naslov: Postano: 15:54 sri, 3. 11. 2010 Naslov: |
    |
|
|
[quote="spot137"]Evo jedan zadatak ako se kome da rijesiti, pa da stavi, jer imamo nesuglasice oko riješenja :D
Bacamo 3 kocke, koje razlikujemo (svaka je druge boje). Koja je vjerojatnost da je na bijeloj kocki pala 4 ako je zbroj svih kocka 13?[/quote]
4/(6)^3
EDIT: krivo shvatia zadatak, pbakic je dobro rijesia :wink:
| spot137 (napisa): | Evo jedan zadatak ako se kome da rijesiti, pa da stavi, jer imamo nesuglasice oko riješenja 
Bacamo 3 kocke, koje razlikujemo (svaka je druge boje). Koja je vjerojatnost da je na bijeloj kocki pala 4 ako je zbroj svih kocka 13? |
4/(6)^3
EDIT: krivo shvatia zadatak, pbakic je dobro rijesia 
Zadnja promjena: some_dude; 16:32 sri, 3. 11. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
 Postano: 16:05 sri, 3. 11. 2010 Naslov: Postano: 16:05 sri, 3. 11. 2010 Naslov: |
    |
|
|
Jel bi mogo neko rjesit zd: koja je najmanja sigma algebra koja sadrzi skupove A={2,5}, B={1,2,4}, C={3,6} omega={1,2,3,4,5,6}.
To je zd iz ovog kolokvija:
http://web.math.hr/nastava/uuv/files/uuv-0607-kol1.pdf
Jel bi mogo neko rjesit zd: koja je najmanja sigma algebra koja sadrzi skupove A={2,5}, B={1,2,4}, C={3,6} omega={1,2,3,4,5,6}.
To je zd iz ovog kolokvija:
http://web.math.hr/nastava/uuv/files/uuv-0607-kol1.pdf
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 16:22 sri, 3. 11. 2010 Naslov: Postano: 16:22 sri, 3. 11. 2010 Naslov: |
    |
|
|
E za ovaj zadatak s kockama ja dobivam nes skroz drugo...
stavimo [latex]\Omega=\{(a,b,c)\in \mathbb{N}^3: a,b,c\leq 6\}[/latex] , [latex]k(\Omega)=6^3
[/latex]
Ako je dogadjaj A={na bijeloj kocki pada 4} i B={zbroj je 13}, onda vrijedi:
[latex]P(A|B)=\frac{P(A\cap B)}{P(B)}[/latex]
brojimo nacine na koje moze pasti zbroj 13:
6,6,1 - 3 nacina
6,5,2 - 6 nacina
6,4,3 - 6 nacina
5,5,3 - 3 nacina
5,4,4 - 3 nacina
=> ukupno 21 nacin za dobit 13 na 3 kocke
ako je na bijeloj kocki 4, moramo prebrojati nacine na koje preostale dvije kocke u zbroju daju 9 (dakle ukupno 13) - to ce nam dati broj elementarnih dogadjaja iz [latex]A\cap B[/latex]:
6,3 - 2 nacina
5,4 - 2 nacina
=> ukupno 4 nacina
[latex]\Rightarrow P(A\cap B)=\frac{4}{6^3}[/latex] i
[latex]P(B)=\frac{21}{6^3}[/latex]
Kad se to podijeli, dobije se [latex]P(A|B)=\frac{4}{21}[/latex]
E za ovaj zadatak s kockama ja dobivam nes skroz drugo...
stavimo 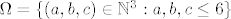 , , 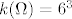
Ako je dogadjaj A={na bijeloj kocki pada 4} i B={zbroj je 13}, onda vrijedi:
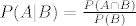
brojimo nacine na koje moze pasti zbroj 13:
6,6,1 - 3 nacina
6,5,2 - 6 nacina
6,4,3 - 6 nacina
5,5,3 - 3 nacina
5,4,4 - 3 nacina
⇒ ukupno 21 nacin za dobit 13 na 3 kocke
ako je na bijeloj kocki 4, moramo prebrojati nacine na koje preostale dvije kocke u zbroju daju 9 (dakle ukupno 13) - to ce nam dati broj elementarnih dogadjaja iz  : :
6,3 - 2 nacina
5,4 - 2 nacina
⇒ ukupno 4 nacina
 i i
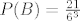
Kad se to podijeli, dobije se 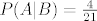
Zadnja promjena: pbakic; 16:24 sri, 3. 11. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 16:22 sri, 3. 11. 2010 Naslov: Postano: 16:22 sri, 3. 11. 2010 Naslov: |
    |
|
|
[quote="eve"]Jel bi mogo neko rjesit zd: koja je najmanja sigma algebra koja sadrzi skupove A={2,5}, B={1,2,4}, C={3,6} omega={1,2,3,4,5,6}.
To je zd iz ovog kolokvija:
http://web.math.hr/nastava/uuv/files/uuv-0607-kol1.pdf[/quote]
{0}-prazan skup
{1,3,4,6}, {3,5,6}, {1,2,4,5}
{2,3,5,6}
{1,2,3,4,6},{1,3,5,6}
i naravno A,B,C i omega
nadam se da nisam nešto zaboravila..
edit:
jesam,razlike i presjeke..jooooj,a sad mi se to neda :D
ima neki kraći način?
| eve (napisa): | Jel bi mogo neko rjesit zd: koja je najmanja sigma algebra koja sadrzi skupove A={2,5}, B={1,2,4}, C={3,6} omega={1,2,3,4,5,6}.
To je zd iz ovog kolokvija:
http://web.math.hr/nastava/uuv/files/uuv-0607-kol1.pdf |
{0}-prazan skup
{1,3,4,6}, {3,5,6}, {1,2,4,5}
{2,3,5,6}
{1,2,3,4,6},{1,3,5,6}
i naravno A,B,C i omega
nadam se da nisam nešto zaboravila..
edit:
jesam,razlike i presjeke..jooooj,a sad mi se to neda 
ima neki kraći način?
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
some_dude
Forumaš(ica)
Pridružen/a: 08. 11. 2009. (16:23:13)
Postovi: (59)16
Spol: 
Lokacija: Zd-Zg
|
 Postano: 16:30 sri, 3. 11. 2010 Naslov: Postano: 16:30 sri, 3. 11. 2010 Naslov: |
    |
|
|
[quote="eve"]Jel bi mogo neko rjesit zd: koja je najmanja sigma algebra koja sadrzi skupove A={2,5}, B={1,2,4}, C={3,6} omega={1,2,3,4,5,6}.
To je zd iz ovog kolokvija:
http://web.math.hr/nastava/uuv/files/uuv-0607-kol1.pdf[/quote]
Trazena sigma algbera mora sadržavati prazan skup, skupove A,B i C te njihove komplemente i sve moguće unije navedenih skupova. Ali bilo bi glupo sada to sve raspisivati. Imaš ovo:
komplement od A: {1,3,4,6}
komplement od B: {3,5,6}
komplement od C: {1,2,4,5}.
Također sa vježbi znamo da ako su A i B iz neke sigma algebre F, tada je i presjek tih skupova i razlika također u F. Sada probaj sam/sama dobiti da u sigma algberi moraju biti {1}, {2}, {3}, {4}, {5} i {6} pa i sve moguće unije tih skupova. Tako dobiješ sve moguće podskupove od omega pa je najmanja sigma algebra koja sadrži A, B i C partitivni skup od omega.
EDIT: Mogu raspisati ako treba...
| eve (napisa): | Jel bi mogo neko rjesit zd: koja je najmanja sigma algebra koja sadrzi skupove A={2,5}, B={1,2,4}, C={3,6} omega={1,2,3,4,5,6}.
To je zd iz ovog kolokvija:
http://web.math.hr/nastava/uuv/files/uuv-0607-kol1.pdf |
Trazena sigma algbera mora sadržavati prazan skup, skupove A,B i C te njihove komplemente i sve moguće unije navedenih skupova. Ali bilo bi glupo sada to sve raspisivati. Imaš ovo:
komplement od A: {1,3,4,6}
komplement od B: {3,5,6}
komplement od C: {1,2,4,5}.
Također sa vježbi znamo da ako su A i B iz neke sigma algebre F, tada je i presjek tih skupova i razlika također u F. Sada probaj sam/sama dobiti da u sigma algberi moraju biti {1}, {2}, {3}, {4}, {5} i {6} pa i sve moguće unije tih skupova. Tako dobiješ sve moguće podskupove od omega pa je najmanja sigma algebra koja sadrži A, B i C partitivni skup od omega.
EDIT: Mogu raspisati ako treba...
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
 Postano: 17:33 sri, 3. 11. 2010 Naslov: Postano: 17:33 sri, 3. 11. 2010 Naslov: |
    |
|
|
[quote="some_dude"]Trazena sigma algbera mora sadržavati prazan skup, skupove A,B i C te njihove komplemente i sve moguće unije navedenih skupova. Ali bilo bi glupo sada to sve raspisivati. Imaš ovo:
komplement od A: {1,3,4,6}
komplement od B: {3,5,6}
komplement od C: {1,2,4,5}.
Također sa vježbi znamo da ako su A i B iz neke sigma algebre F, tada je i presjek tih skupova i razlika također u F. Sada probaj sam/sama dobiti da u sigma algberi moraju biti {1}, {2}, {3}, {4}, {5} i {6} pa i sve moguće unije tih skupova. Tako dobiješ sve moguće podskupove od omega pa je najmanja sigma algebra koja sadrži A, B i C partitivni skup od omega.
EDIT: Mogu raspisati ako treba...[/quote]
Da li to onda znaci da sigma algebra uvijek sadrzi sve podskupove od omega?
| some_dude (napisa): | Trazena sigma algbera mora sadržavati prazan skup, skupove A,B i C te njihove komplemente i sve moguće unije navedenih skupova. Ali bilo bi glupo sada to sve raspisivati. Imaš ovo:
komplement od A: {1,3,4,6}
komplement od B: {3,5,6}
komplement od C: {1,2,4,5}.
Također sa vježbi znamo da ako su A i B iz neke sigma algebre F, tada je i presjek tih skupova i razlika također u F. Sada probaj sam/sama dobiti da u sigma algberi moraju biti {1}, {2}, {3}, {4}, {5} i {6} pa i sve moguće unije tih skupova. Tako dobiješ sve moguće podskupove od omega pa je najmanja sigma algebra koja sadrži A, B i C partitivni skup od omega.
EDIT: Mogu raspisati ako treba... |
Da li to onda znaci da sigma algebra uvijek sadrzi sve podskupove od omega?
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 17:55 sri, 3. 11. 2010 Naslov: Postano: 17:55 sri, 3. 11. 2010 Naslov: |
    |
|
|
kada sam napisala prošli post mi je sinuo zadatak s vježbi i mislim da ne mora sadržavati 2^n elemenata, jer se traži "najmanja". mislim,ja to ne kužim skroz,ali evo zadatka s vježbi,isti tekst zadataka a skupovi su {1},{1,2},{1,2,3},{1,2,3,4}, a najmanja sigma algebra toga je omega={1,2,3,4,5}-zadana u zadatku,prazan skup,ti zadani skupovi i {1},{2},{4},{3},{5}.
sad,ovdje npr nije u njoj {1,2,3,4}/{1,2}={3,4} napisan eksplicitno, ali je u njoj kao {3}U{4}, jer kod sigma algebre vrijedi A1,A2 e F -> A1uA2 e F
isto tako za komplemente
sve ja to kužim,ali neznam kako odrediti točne skupove.. pa može pomoć??
edit:i može rješenje 1. i 2. zadatka u http://web.math.hr/nastava/uuv/files/uuv-0607-kol1.pdf ako ne tražim previše? :)
kada sam napisala prošli post mi je sinuo zadatak s vježbi i mislim da ne mora sadržavati 2^n elemenata, jer se traži "najmanja". mislim,ja to ne kužim skroz,ali evo zadatka s vježbi,isti tekst zadataka a skupovi su {1},{1,2},{1,2,3},{1,2,3,4}, a najmanja sigma algebra toga je omega={1,2,3,4,5}-zadana u zadatku,prazan skup,ti zadani skupovi i {1},{2},{4},{3},{5}.
sad,ovdje npr nije u njoj {1,2,3,4}/{1,2}={3,4} napisan eksplicitno, ali je u njoj kao {3}U{4}, jer kod sigma algebre vrijedi A1,A2 e F -> A1uA2 e F
isto tako za komplemente
sve ja to kužim,ali neznam kako odrediti točne skupove.. pa može pomoć??
edit:i može rješenje 1. i 2. zadatka u http://web.math.hr/nastava/uuv/files/uuv-0607-kol1.pdf ako ne tražim previše? 
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 18:18 sri, 3. 11. 2010 Naslov: Postano: 18:18 sri, 3. 11. 2010 Naslov: |
    |
|
|
Treba sadrzavati 2^n, al ne za n=broj elemenata u omega, nego nekakav n...
A za ovaj zadatak:
ako su zadani {1},{1,2},{1,2,3},{1,2,3,4} i omega={1,2,3,4,5}
ocito da su u toj sigma algebri i skupovi
{1},{2},{3},{4},{5} (kao razlike ovih uzastopnih)
E sad, kad imamo ovakve skupove (particiju), onda je jasno da svaki podskup od omega mora biti u sigma algebri, jer se moze dobiti kao unija nekih od ovih 5 skupova => u ovom slucaju s.algebra=partitivni(omega)
[size=9][color=#999999]Added after 2 minutes:[/color][/size]
Evo 06/07 stize uskoro :)
[size=9][color=#999999]Added after 11 minutes:[/color][/size]
1) pretpostavimo da postoji takav niz disjunktnih dogadjaja. Tada je
P(UAi) = suma P(Ai) (naravno i ide od 0 do beskonacno)
ocito vrijedi
1>=P(UAi) = suma P(Ai)= suma 1/(2i+1)= beskonacno
(s analize 2 znamo da divergira ovaj red s desne strane :))
dakle dobivamo 1>=oo (beskonacno :)), sto je kontradikcija, tj. takav skup ne postoji
2) (da ne bi mor'o u texu, p=presjek, u=unija)
Ocito u ovakvoj sigma-algebri moraju biti sljedeci skupovi:
{2}
{5} (kao A \ ApB)
{1,4} (AuB \ A)
{3,6}
Sad samo napravimo sve moguce unije ovih skupova (ima ih 16) i provjerimo jesu li A,B,C medju tim skupovima (sve moguce unije neke particije su sigurno sigma-algebra)
unija moze imati...
0 clanova : prazan skup
1 clan: {2},{5},{1,4},{3,6}
2 clana: {2,5},{1,2,4},{2,3,6},{1,4,5},{3,5,6},{1,3,4,6}
3 clana: {1,3,4,5,6},{1,2,3,4,6},{2,3,5,6},{1,2,4,5}
4 clana: {1,2,3,4,5,6}
vidi se da su nasi A={2,5}, B={1,2,4} , C={3,6} medju ovim skupovima, a ovo je sigma algebra => to je to :D
Treba sadrzavati 2^n, al ne za n=broj elemenata u omega, nego nekakav n...
A za ovaj zadatak:
ako su zadani {1},{1,2},{1,2,3},{1,2,3,4} i omega={1,2,3,4,5}
ocito da su u toj sigma algebri i skupovi
{1},{2},{3},{4},{5} (kao razlike ovih uzastopnih)
E sad, kad imamo ovakve skupove (particiju), onda je jasno da svaki podskup od omega mora biti u sigma algebri, jer se moze dobiti kao unija nekih od ovih 5 skupova ⇒ u ovom slucaju s.algebra=partitivni(omega)
Added after 2 minutes:
Evo 06/07 stize uskoro 
Added after 11 minutes:
1) pretpostavimo da postoji takav niz disjunktnih dogadjaja. Tada je
P(UAi) = suma P(Ai) (naravno i ide od 0 do beskonacno)
ocito vrijedi
1>=P(UAi) = suma P(Ai)= suma 1/(2i+1)= beskonacno
(s analize 2 znamo da divergira ovaj red s desne strane  ) )
dakle dobivamo 1>=oo (beskonacno  ), sto je kontradikcija, tj. takav skup ne postoji ), sto je kontradikcija, tj. takav skup ne postoji
2) (da ne bi mor'o u texu, p=presjek, u=unija)
Ocito u ovakvoj sigma-algebri moraju biti sljedeci skupovi:
{2}
{5} (kao A \ ApB)
{1,4} (AuB \ A)
{3,6}
Sad samo napravimo sve moguce unije ovih skupova (ima ih 16) i provjerimo jesu li A,B,C medju tim skupovima (sve moguce unije neke particije su sigurno sigma-algebra)
unija moze imati...
0 clanova : prazan skup
1 clan: {2},{5},{1,4},{3,6}
2 clana: {2,5},{1,2,4},{2,3,6},{1,4,5},{3,5,6},{1,3,4,6}
3 clana: {1,3,4,5,6},{1,2,3,4,6},{2,3,5,6},{1,2,4,5}
4 clana: {1,2,3,4,5,6}
vidi se da su nasi A={2,5}, B={1,2,4} , C={3,6} medju ovim skupovima, a ovo je sigma algebra ⇒ to je to 
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 18:23 sri, 3. 11. 2010 Naslov: Postano: 18:23 sri, 3. 11. 2010 Naslov: |
    |
|
|
jel je sada najmanja sigma algebra ({2} ,{5}, {1,4},{3,6},) ili još A,B,C i ove sve unije?
i naravno omega i prazan skup
PS.puno hvalaaaa
jel je sada najmanja sigma algebra ({2} ,{5}, {1,4},{3,6},) ili još A,B,C i ove sve unije?
i naravno omega i prazan skup
PS.puno hvalaaaa
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 19:03 sri, 3. 11. 2010 Naslov: Postano: 19:03 sri, 3. 11. 2010 Naslov: |
    |
|
|
Nije bas istina da se svi podskupovi od omega trebaju moc prikazat pomocu elemenata sigma-algebre...
Primjer
prazan skup, {1,2,3}, {4,5,6} i {1,2,3,4,5,6} cine sigma algebru na skupu {1,2,3,4,5,6}
(ocito mozes prikazat samo ova 4 skupa pomocu njih)
Fora je u tome da se svaki element sigma algebre moze dobiti pomocu operacija s ostalim elementima sigma-algebre.
Vrijedi i obrat: ako se neki skup moze dobiti pomocu elemenata sigma algebre, onda je on u toj s.algebri...
To smo koristili u prethodnom zadatku; nasli smo neke skupove koji moraju bit u salgebri (onih 5) i skuzili da sve njihove unije takodjer moraju bit...
Nije bas istina da se svi podskupovi od omega trebaju moc prikazat pomocu elemenata sigma-algebre...
Primjer
prazan skup, {1,2,3}, {4,5,6} i {1,2,3,4,5,6} cine sigma algebru na skupu {1,2,3,4,5,6}
(ocito mozes prikazat samo ova 4 skupa pomocu njih)
Fora je u tome da se svaki element sigma algebre moze dobiti pomocu operacija s ostalim elementima sigma-algebre.
Vrijedi i obrat: ako se neki skup moze dobiti pomocu elemenata sigma algebre, onda je on u toj s.algebri...
To smo koristili u prethodnom zadatku; nasli smo neke skupove koji moraju bit u salgebri (onih 5) i skuzili da sve njihove unije takodjer moraju bit...
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
 Postano: 19:48 sri, 3. 11. 2010 Naslov: Postano: 19:48 sri, 3. 11. 2010 Naslov: |
    |
|
|
[quote="pbakic"]
2) (da ne bi mor'o u texu, p=presjek, u=unija)
Ocito u ovakvoj sigma-algebri moraju biti sljedeci skupovi:
{2}
{5} (kao A \ ApB)
{1,4} (AuB \ A)
{3,6}
Sad samo napravimo sve moguce unije ovih skupova (ima ih 16) i provjerimo jesu li A,B,C medju tim skupovima (sve moguce unije neke particije su sigurno sigma-algebra)
unija moze imati...
0 clanova : prazan skup
1 clan: {2},{5},{1,4},{3,6}
2 clana: {2,5},{1,2,4},{2,3,6},{1,4,5},{3,5,6},{1,3,4,6}
3 clana: {1,3,4,5,6},{1,2,3,4,6},{2,3,5,6},{1,2,4,5}
4 clana: {1,2,3,4,5,6}
vidi se da su nasi A={2,5}, B={1,2,4} , C={3,6} medju ovim skupovima, a ovo je sigma algebra => to je to :D[/quote]
Ja imam jedno glupo pitanje. Nisam skuzila kako se dobiju ove unije. Pa jel bi mogao netko to raspisat? barem kako ide za uniju sa npr. 2 clana...
:oops: :oops:
| pbakic (napisa): |
2) (da ne bi mor'o u texu, p=presjek, u=unija)
Ocito u ovakvoj sigma-algebri moraju biti sljedeci skupovi:
{2}
{5} (kao A \ ApB)
{1,4} (AuB \ A)
{3,6}
Sad samo napravimo sve moguce unije ovih skupova (ima ih 16) i provjerimo jesu li A,B,C medju tim skupovima (sve moguce unije neke particije su sigurno sigma-algebra)
unija moze imati...
0 clanova : prazan skup
1 clan: {2},{5},{1,4},{3,6}
2 clana: {2,5},{1,2,4},{2,3,6},{1,4,5},{3,5,6},{1,3,4,6}
3 clana: {1,3,4,5,6},{1,2,3,4,6},{2,3,5,6},{1,2,4,5}
4 clana: {1,2,3,4,5,6}
vidi se da su nasi A={2,5}, B={1,2,4} , C={3,6} medju ovim skupovima, a ovo je sigma algebra ⇒ to je to  |
Ja imam jedno glupo pitanje. Nisam skuzila kako se dobiju ove unije. Pa jel bi mogao netko to raspisat? barem kako ide za uniju sa npr. 2 clana...
 
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 20:11 sri, 3. 11. 2010 Naslov: Postano: 20:11 sri, 3. 11. 2010 Naslov: |
    |
|
|
je li ovo točno:
a={1,3,4}, b={2,4,6}, c={5}
namanja sigma algebra:
{4},{1,3},{2,6},{5}
prazan skup, {1,3,4}, {2,4,6},{4,5}, {1,2,3,6},{1,3,5}, {2,5,6},
{1,2,3,4,6},{2,4,5,6},{1,2,3,5,6},omega
i {1,3,4,5}
i još ovo: http://web.math.hr/nastava/uuv/files/uuv-0708-kol1.pdf
drugi zadatak:
vidimo da je [0,1] podskup [0,2] ... podskup [0,5]
pa mi se čini,ali samo čini :D ,da je najmanja sigma algebra
prazan skup,[0,5],<5,10],omega
pretpostavljam da nije točno,pa ako može točno rješenje? :?
je li ovo točno:
a={1,3,4}, b={2,4,6}, c={5}
namanja sigma algebra:
{4},{1,3},{2,6},{5}
prazan skup, {1,3,4}, {2,4,6},{4,5}, {1,2,3,6},{1,3,5}, {2,5,6},
{1,2,3,4,6},{2,4,5,6},{1,2,3,5,6},omega
i {1,3,4,5}
i još ovo: http://web.math.hr/nastava/uuv/files/uuv-0708-kol1.pdf
drugi zadatak:
vidimo da je [0,1] podskup [0,2] ... podskup [0,5]
pa mi se čini,ali samo čini  ,da je najmanja sigma algebra ,da je najmanja sigma algebra
prazan skup,[0,5],<5,10],omega
pretpostavljam da nije točno,pa ako može točno rješenje? 
|
|
| [Vrh] |
|
|




















