| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
|
| [Vrh] |
|
Lanek_
Forumaš(ica)

Pridružen/a: 22. 10. 2010. (18:51:42)
Postovi: (31)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 21:30 ned, 26. 12. 2010 Naslov: Postano: 21:30 ned, 26. 12. 2010 Naslov: |
    |
|
|
A zašto ne prva grupa? :P (Mislim, princip je isti, pa pitam... :))
U svakom slučaju, čak sam, mislim, i riješio to tu negdje... aha, evo te! :D Daklem, [url=http://degiorgi.math.hr/forum/viewtopic.php?p=147246#147246]ovdje[/url] sam svojedobno napisao to što ti tu zahtijevaš. :D
A zašto ne prva grupa?  (Mislim, princip je isti, pa pitam... (Mislim, princip je isti, pa pitam...  ) )
U svakom slučaju, čak sam, mislim, i riješio to tu negdje... aha, evo te!  Daklem, ovdje sam svojedobno napisao to što ti tu zahtijevaš. Daklem, ovdje sam svojedobno napisao to što ti tu zahtijevaš. 
|
|
| [Vrh] |
|
Lanek_
Forumaš(ica)

Pridružen/a: 22. 10. 2010. (18:51:42)
Postovi: (31)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 15:01 pon, 27. 12. 2010 Naslov: Postano: 15:01 pon, 27. 12. 2010 Naslov: |
    |
|
|
Dobro, gotovo pa kriminalna nepreciznost aside :P (nije [latex]=[/latex] nego [latex]\to[/latex], a ima i još jedan tipfeler :P), stvar je zapravo slična onome što ste vjerojatno radili na dosta zadataka.
Možda će biti lakše ako ovako napišemo. Dakle, znamo da za [latex]t\to 0[/latex] vrijedi [latex]\displaystyle\frac{e^t+e^{-t}-2}{t^2}\to 1[/latex]. Sad uvrstimo [latex]x\ln 4=:t[/latex]. Vidi se da je [latex]t\to 0[/latex] ekvivalentno s [latex]x\to 0[/latex] - to nam je bitno. Naime, onda znamo da je [latex]1=\displaystyle\lim_{t\to 0}\frac{e^t+e^{-t}-2}{t^2}=\lim_{x\to 0}\frac{e^t+e^{-t}-2}{t^2}[/latex]. Umjesto [latex]t[/latex] sad pišemo [latex]x\ln 4[/latex] i gotovo direktno dobivamo [latex]\displaystyle\lim_{x\to 0}\frac{4^x+4^{-x}-2}{(x\ln 4)^2}=1[/latex]. No, mi tražimo [latex]\displaystyle\lim_{x\to 0}\frac{4^x+4^{-x}-2}{x^2}[/latex], što znači da gornji izraz množimo s [latex]\ln^2 4[/latex] (da bismo dobili ono što tražimo) - od tuda to množenje koje te muči. :)
Iz [latex]\displaystyle\frac{4^x+4^{-x}-2}{(x\ln 4)^2}\to 1[/latex] imamo, dakle, [latex]\displaystyle\frac{4^x+4^{-x}-2}{(x\ln 4)^2}\ln^2 4\to \ln^2 4[/latex], tj. kad se stvar pokrati [latex]\displaystyle\frac{4^x+4^{-x}-2}{x^2}\to \ln^2 4[/latex]. Eto, sad smo gotovi. (Postupak je u svakom slučaju sasvim u redu. Iako, sjetiti se toga... moram reći da sam sumnjičav. :) But that's just me. :))
Dobro, gotovo pa kriminalna nepreciznost aside  (nije (nije  nego nego  , a ima i još jedan tipfeler , a ima i još jedan tipfeler  ), stvar je zapravo slična onome što ste vjerojatno radili na dosta zadataka. ), stvar je zapravo slična onome što ste vjerojatno radili na dosta zadataka.
Možda će biti lakše ako ovako napišemo. Dakle, znamo da za 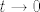 vrijedi vrijedi 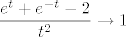 . Sad uvrstimo . Sad uvrstimo 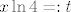 . Vidi se da je . Vidi se da je 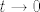 ekvivalentno s ekvivalentno s 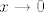 - to nam je bitno. Naime, onda znamo da je - to nam je bitno. Naime, onda znamo da je 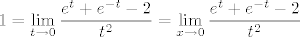 . Umjesto . Umjesto  sad pišemo sad pišemo 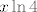 i gotovo direktno dobivamo i gotovo direktno dobivamo 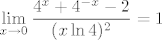 . No, mi tražimo . No, mi tražimo 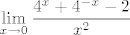 , što znači da gornji izraz množimo s , što znači da gornji izraz množimo s 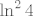 (da bismo dobili ono što tražimo) - od tuda to množenje koje te muči. (da bismo dobili ono što tražimo) - od tuda to množenje koje te muči. 
Iz 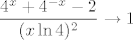 imamo, dakle, imamo, dakle, 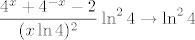 , tj. kad se stvar pokrati , tj. kad se stvar pokrati 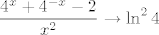 . Eto, sad smo gotovi. (Postupak je u svakom slučaju sasvim u redu. Iako, sjetiti se toga... moram reći da sam sumnjičav. . Eto, sad smo gotovi. (Postupak je u svakom slučaju sasvim u redu. Iako, sjetiti se toga... moram reći da sam sumnjičav.  But that's just me. But that's just me.  ) )
|
|
| [Vrh] |
|
Lanek_
Forumaš(ica)

Pridružen/a: 22. 10. 2010. (18:51:42)
Postovi: (31)16
|
|
| [Vrh] |
|
kre5o
Forumaš(ica)
Pridružen/a: 14. 09. 2009. (22:20:52)
Postovi: (32)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 18:05 sri, 29. 12. 2010 Naslov: Postano: 18:05 sri, 29. 12. 2010 Naslov: |
    |
|
|
A gle, kakve limese znamo (tj. kakve možemo naći u tablici)? Uglavnom one gdje [latex]x\to +\infty[/latex] i [latex]x\to 0[/latex] (ne znam ima li neki u kojem [latex]x\to 1[/latex]). Stoga, ideja je dovesti stvar na neki od njih. E, sad, uzevši to u obzir, čini se smisleno da umjesto [latex]x\to 7[/latex] gledamo [latex]x-7\to 0[/latex]. Dakle, idemo uzeti [latex]t:=x-7[/latex].
Sad je [latex]t\to 0[/latex] ekvivalentno s [latex]x\to 7[/latex], pa tražimo [latex]\displaystyle\lim_{t\to 0}\frac{2-\sqrt{x-3}}{x^2-49}[/latex]. Sad ćemo umjesto [latex]x[/latex] pisati [latex]t+7[/latex] i dobiti [latex]\displaystyle\lim_{t\to 0}\frac{2-\sqrt{t+4}}{t^2+14t}[/latex].
E, a ovo nam se već sviđa. :) Sad znamo kako dalje - množimo i brojnik i nazivnik s [latex]2+\sqrt{t+4}[/latex] i dobivamo razlomak [latex]\displaystyle\frac{-t}{t(t+14)(2+\sqrt{t+4})}[/latex]. Pokratimo [latex]t[/latex] i sad nam je limes jasan: iznosi [latex]\displaystyle-\frac{1}{56}[/latex].
Evo, to je to. Ta se ideja inače javlja u dosta zadataka, pa ju je valjda korisno zapamtiti. :)
(Inače, ne znam treba li komentirati, valjda ne, ali za svaki slučaj da spomenem, kad sam se sad sjetio: tražiti ovaj limes ima smisla u kontekstu definiranosti jer je funkcija [latex]\displaystyle f(x)=\frac{2-\sqrt{x-3}}{x^2-49}[/latex] definirana na nekoj otvorenoj okolini točke [latex]7[/latex]. Na primjer, tražiti [latex]\displaystyle\lim_{x\to 3}\frac{2-\sqrt{x-3}}{x^2-49}[/latex] ne bi imalo smisla tražiti jer gornja funkcija [latex]f[/latex] nije definirana ni za koji [latex]x<3[/latex]. Imalo bi smisla tražiti limes kad [latex]x\to 3+[/latex], ali to je druga stvar.)
A gle, kakve limese znamo (tj. kakve možemo naći u tablici)? Uglavnom one gdje 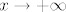 i i 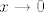 (ne znam ima li neki u kojem (ne znam ima li neki u kojem 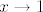 ). Stoga, ideja je dovesti stvar na neki od njih. E, sad, uzevši to u obzir, čini se smisleno da umjesto ). Stoga, ideja je dovesti stvar na neki od njih. E, sad, uzevši to u obzir, čini se smisleno da umjesto 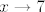 gledamo gledamo 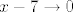 . Dakle, idemo uzeti . Dakle, idemo uzeti 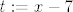 . .
Sad je 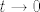 ekvivalentno s ekvivalentno s 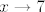 , pa tražimo , pa tražimo 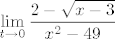 . Sad ćemo umjesto . Sad ćemo umjesto  pisati pisati 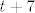 i dobiti i dobiti 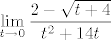 . .
E, a ovo nam se već sviđa.  Sad znamo kako dalje - množimo i brojnik i nazivnik s Sad znamo kako dalje - množimo i brojnik i nazivnik s 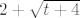 i dobivamo razlomak i dobivamo razlomak 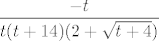 . Pokratimo . Pokratimo  i sad nam je limes jasan: iznosi i sad nam je limes jasan: iznosi 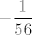 . .
Evo, to je to. Ta se ideja inače javlja u dosta zadataka, pa ju je valjda korisno zapamtiti. 
(Inače, ne znam treba li komentirati, valjda ne, ali za svaki slučaj da spomenem, kad sam se sad sjetio: tražiti ovaj limes ima smisla u kontekstu definiranosti jer je funkcija 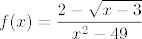 definirana na nekoj otvorenoj okolini točke definirana na nekoj otvorenoj okolini točke 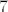 . Na primjer, tražiti . Na primjer, tražiti 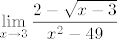 ne bi imalo smisla tražiti jer gornja funkcija ne bi imalo smisla tražiti jer gornja funkcija  nije definirana ni za koji nije definirana ni za koji 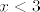 . Imalo bi smisla tražiti limes kad . Imalo bi smisla tražiti limes kad 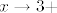 , ali to je druga stvar.) , ali to je druga stvar.)
|
|
| [Vrh] |
|
kre5o
Forumaš(ica)
Pridružen/a: 14. 09. 2009. (22:20:52)
Postovi: (32)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 19:02 sri, 29. 12. 2010 Naslov: Postano: 19:02 sri, 29. 12. 2010 Naslov: |
    |
|
|
Sad sam shvatio, moj predivni rad i mudre pouke na stranu :D, ima i znatno lakši način rješavanja, ne treba uopće uvoditi supstituciju - samo pomnoži i brojnik i nazivnik s [latex]2+\sqrt{x-3}[/latex], kako ste to već radili na puno zadataka. Tada imamo [latex]\displaystyle\frac{7-x}{(x-7)(x+7)(2+\sqrt{x-3})}[/latex]. [latex]x-7[/latex] se pokrati i onda limes lako dobivamo. Naravno, i dalje iznosi [latex]\displaystyle -\frac{1}{(7+7)(2+\sqrt{7-3})}=-\frac{1}{56}[/latex]. :P
Sorry na ovom nepotrebnom kompliciranju. :)
Sad sam shvatio, moj predivni rad i mudre pouke na stranu  , ima i znatno lakši način rješavanja, ne treba uopće uvoditi supstituciju - samo pomnoži i brojnik i nazivnik s , ima i znatno lakši način rješavanja, ne treba uopće uvoditi supstituciju - samo pomnoži i brojnik i nazivnik s 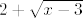 , kako ste to već radili na puno zadataka. Tada imamo , kako ste to već radili na puno zadataka. Tada imamo 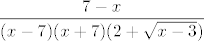 . . 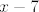 se pokrati i onda limes lako dobivamo. Naravno, i dalje iznosi se pokrati i onda limes lako dobivamo. Naravno, i dalje iznosi 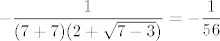 . . 
Sorry na ovom nepotrebnom kompliciranju. 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 18:00 čet, 30. 12. 2010 Naslov: Postano: 18:00 čet, 30. 12. 2010 Naslov: |
    |
|
|
A sa ln je uvijek ista finta: kad imas ln(f(x)) gdje f(x) tezi u 1, onda je to isto kao da imas f(x)-1. Tocnije, [latex]\displaystyle \lim_{x\rightarrow 1} \frac{\ln x}{x-1}[/latex]
Iz toga vidis da je korisno sve pomnoziti i podijeliti s cosx-1, pa dobijemo
[latex]\frac{\sin^2 x + x^2}{\cos x -1}\frac{\cos x - 1}{\ln(\cos x)}[/latex]
Sad ovaj desni razlomak tezi u 1 (zbog ovog limesa gore), pa promatramo samo lijevi. Tu nam je ocito dobro podijelit i pomnozit s x^2, jer znamo [latex]\displaystyle \lim_{x\rightarrow 0} \frac{1-\cos x}{x^2}=\frac{1}{2}[/latex]
Sad imamo znaci
[latex]\frac{\sin^2 x + x^2}{x^2}\frac{x^2}{\cos x - 1}[/latex]
Prvi razlomcic ocito ide u 2, a drugi u -2, pa ukupno sve ide u -4
A sa ln je uvijek ista finta: kad imas ln(f(x)) gdje f(x) tezi u 1, onda je to isto kao da imas f(x)-1. Tocnije, 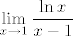
Iz toga vidis da je korisno sve pomnoziti i podijeliti s cosx-1, pa dobijemo
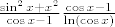
Sad ovaj desni razlomak tezi u 1 (zbog ovog limesa gore), pa promatramo samo lijevi. Tu nam je ocito dobro podijelit i pomnozit s x^2, jer znamo 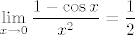
Sad imamo znaci
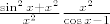
Prvi razlomcic ocito ide u 2, a drugi u -2, pa ukupno sve ide u -4
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 16:23 sub, 1. 1. 2011 Naslov: Postano: 16:23 sub, 1. 1. 2011 Naslov: |
    |
|
|
[quote="pbakic"]A sa ln je uvijek ista finta: kad imas ln(f(x)) gdje f(x) tezi u 1, onda je to isto kao da imas f(x)-1. Tocnije, [latex]\displaystyle \lim_{x\rightarrow 1} \frac{\ln x}{x-1}[/latex]
Iz toga vidis da je korisno sve pomnoziti i podijeliti s cosx-1, pa dobijemo
[latex]\frac{\sin^2 x + x^2}{\cos x -1}\frac{\cos x - 1}{\ln(\cos x)}[/latex]
Sad ovaj desni razlomak tezi u 1 (zbog ovog limesa gore), pa promatramo samo lijevi. Tu nam je ocito dobro podijelit i pomnozit s x^2, jer znamo [latex]\displaystyle \lim_{x\rightarrow 0} \frac{1-\cos x}{x^2}=\frac{1}{2}[/latex]
Sad imamo znaci
[latex]\frac{\sin^2 x + x^2}{x^2}\frac{x^2}{\cos x - 1}[/latex]
HVALA NE POMOCI!
Ako se nekome da, zamolila bih da objasni kako u wolf.izracunati limese, to bi mi dobro doslo, da ne pitam tu bas za rezultat svakog zadatka cijeg rjesenja nemam.
Zanima me 5. zadatak s kolokvija 2007. :
lim (ch ( 1/ sq(X) ))^ x , limes tezi u +BESK.
sq = KORJEN
Nadam se da je razumljivo, znaci rijecimo jos: kosinus hiper. ( 1 kroz korjen x,) pa sve to na x.
[quote="pbakic"]A sa ln je uvijek ista finta: kad imas ln(f(x)) gdje f(x) tezi u 1, onda je to isto kao da imas f(x)-1. Tocnije, 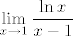
Iz toga vidis da je korisno sve pomnoziti i podijeliti s cosx-1, pa dobijemo
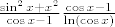
Sad ovaj desni razlomak tezi u 1 (zbog ovog limesa gore), pa promatramo samo lijevi. Tu nam je ocito dobro podijelit i pomnozit s x^2, jer znamo 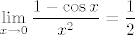
Sad imamo znaci
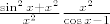
HVALA NE POMOCI!
Ako se nekome da, zamolila bih da objasni kako u wolf.izracunati limese, to bi mi dobro doslo, da ne pitam tu bas za rezultat svakog zadatka cijeg rjesenja nemam.
Zanima me 5. zadatak s kolokvija 2007. :
lim (ch ( 1/ sq(X) ))^ x , limes tezi u +BESK.
sq = KORJEN
Nadam se da je razumljivo, znaci rijecimo jos: kosinus hiper. ( 1 kroz korjen x,) pa sve to na x.
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 17:14 sub, 1. 1. 2011 Naslov: Postano: 17:14 sub, 1. 1. 2011 Naslov: |
    |
|
|
Kada koristiš Wolfram Alphu za limese, moraš napisati "limit *varijabla* to *vrijednost*" i onda pišeš izraz kojemu tražiš limes. Jedino zna biti problem kada tipkaš imena nekih funkcija; npr., u ovom primjeru ch je zapravo cosh za Wolfram Alphu, jer on "ch" interpretira kao kotangens hiperbolni.
Evo ti link kako to izgleda: [url=http://www.wolframalpha.com/input/?i=limit+x+to+infinity+%28ch%281%2Fsqrt%28x%29%29^x]primjer[/url].
Ako varijabla teži u (plus) beskonačno, onda možeš navesti samo "limit", ali onda je moguće da navede više mogućih limesa, kao npr., [url=http://www.wolframalpha.com/input/?i=limit+%28cosh%281%2Fsqrt%28x%29%29^x]ovdje[/url].
A sad na zadatak:
[latex]\displaystyle\lim_{x\to +\infty}(ch(\frac{1}{\sqrt x}))^x=[1^+^\infty]=e^{\displaystyle\lim_{x\to +\infty}(ch(\frac{1}{\sqrt x})-1)*x}=e^{\displaystyle\lim_{x\to +\infty}\frac{ch(\frac{1}{\sqrt x})-1}{(\frac{1}{\sqrt x})^2}}=e^\frac{1}{2}=\sqrt e[/latex]
U početku je dobro provjeriti je li ovo oblika [latex][1^+^\infty][/latex] (jer imamo bazu i eksponent). Uočavamo da je to traženi oblik i raspišemo formulu po eksponentu (a baza je e). Sada, kako nam je ch najviše problematičan, želimo po poznatoj formuli namjestiti nazivnik tako da u njemu imamo [latex](\frac{1}{\sqrt x})^2[/latex], a to možemo raditi jer izraz unutar funkcije ch teži u 0 (baš kao i u općoj formuli). Ali u ovom primjeru nemamo potrebe za namještanjem jer je taj izraz recipročna vrijednost samog x-a, kojeg imamo kao jedan od faktora. (Ako to ne primijetiš, nije problem - samo namjesti nazivnik kakav ti odgovara i, kada pomnožiš izraz sa nazivnikom (da izraz ostane isti; sve množiš i dijeliš s istim izrazom), "skratit" će se s x-om.) Limes je sada poznat.
Kada koristiš Wolfram Alphu za limese, moraš napisati "limit *varijabla* to *vrijednost*" i onda pišeš izraz kojemu tražiš limes. Jedino zna biti problem kada tipkaš imena nekih funkcija; npr., u ovom primjeru ch je zapravo cosh za Wolfram Alphu, jer on "ch" interpretira kao kotangens hiperbolni.
Evo ti link kako to izgleda: primjer.
Ako varijabla teži u (plus) beskonačno, onda možeš navesti samo "limit", ali onda je moguće da navede više mogućih limesa, kao npr., ovdje.
A sad na zadatak:
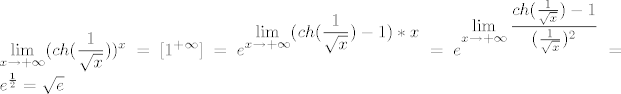
U početku je dobro provjeriti je li ovo oblika 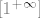 (jer imamo bazu i eksponent). Uočavamo da je to traženi oblik i raspišemo formulu po eksponentu (a baza je e). Sada, kako nam je ch najviše problematičan, želimo po poznatoj formuli namjestiti nazivnik tako da u njemu imamo (jer imamo bazu i eksponent). Uočavamo da je to traženi oblik i raspišemo formulu po eksponentu (a baza je e). Sada, kako nam je ch najviše problematičan, želimo po poznatoj formuli namjestiti nazivnik tako da u njemu imamo 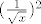 , a to možemo raditi jer izraz unutar funkcije ch teži u 0 (baš kao i u općoj formuli). Ali u ovom primjeru nemamo potrebe za namještanjem jer je taj izraz recipročna vrijednost samog x-a, kojeg imamo kao jedan od faktora. (Ako to ne primijetiš, nije problem - samo namjesti nazivnik kakav ti odgovara i, kada pomnožiš izraz sa nazivnikom (da izraz ostane isti; sve množiš i dijeliš s istim izrazom), "skratit" će se s x-om.) Limes je sada poznat. , a to možemo raditi jer izraz unutar funkcije ch teži u 0 (baš kao i u općoj formuli). Ali u ovom primjeru nemamo potrebe za namještanjem jer je taj izraz recipročna vrijednost samog x-a, kojeg imamo kao jedan od faktora. (Ako to ne primijetiš, nije problem - samo namjesti nazivnik kakav ti odgovara i, kada pomnožiš izraz sa nazivnikom (da izraz ostane isti; sve množiš i dijeliš s istim izrazom), "skratit" će se s x-om.) Limes je sada poznat.
|
|
| [Vrh] |
|
Buki
Forumaš(ica)

Pridružen/a: 17. 10. 2010. (20:15:17)
Postovi: (56)16
|
 Postano: 14:48 sri, 5. 1. 2011 Naslov: Postano: 14:48 sri, 5. 1. 2011 Naslov: |
    |
|
|
[quote="mornik"]Evo hint :) :
Limes od [latex]\displaystyle\frac{x^2}{\tan(x^2)}[/latex] znaš. Znaš i limes od [latex]\displaystyle\frac{x^2}{\sin(x^2)}[/latex]. U brojniku, [latex](\tan(x)-\sin(x))^2=\tan^2(x)\cdot\displaystyle(1-\cos(x))^2[/latex]. To znaš usporediti s [latex]x^6[/latex].
E, sad, kad pomnožimo ta tri limesa koja smo gore spomenuli, dobivamo traženi limes. Ili? :)
Reci ako treba još šta.[/quote]
zanima me koliko iznose ti navedeni limes, i jel se na kolokviju kao poznati limesi priznaju samo oni iz tablica ili i oni koje smo na vjezbama radili?
| mornik (napisa): | Evo hint  : :
Limes od 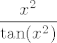 znaš. Znaš i limes od znaš. Znaš i limes od 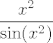 . U brojniku, . U brojniku, 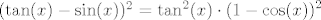 . To znaš usporediti s . To znaš usporediti s 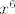 . .
E, sad, kad pomnožimo ta tri limesa koja smo gore spomenuli, dobivamo traženi limes. Ili? 
Reci ako treba još šta. |
zanima me koliko iznose ti navedeni limes, i jel se na kolokviju kao poznati limesi priznaju samo oni iz tablica ili i oni koje smo na vjezbama radili?
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 15:13 sri, 5. 1. 2011 Naslov: Postano: 15:13 sri, 5. 1. 2011 Naslov: |
    |
|
|
Iznose [latex]1[/latex], [latex]1[/latex] i [latex]1\cdot 0.25=0.25[/latex], ako se ne varam. Mislim, to ti zbilja nije teško izračunati, ne znam baš što predstavlja problem... :) Znaš da [latex]\displaystyle\frac{\sin(x)}{x}\to 1[/latex], pa i [latex]\displaystyle\frac{\tan(x)}{x}=\cos(x)\cdot\frac{\sin(x)}{x}\to 1\cdot 1=1[/latex]. Sad onda znaš i limese od [latex]\displaystyle\frac{x^2}{\tan(x^2)}[/latex], [latex]\displaystyle\frac{x^2}{\sin(x^2)}[/latex] (primijeti da [latex]x\to 0 \Leftrightarrow x^2\to 0[/latex], pa možeš formalno uvesti supstituciju [latex]t:=x^2[/latex]). Za ovaj treći limes, znaš da [latex]\displaystyle\frac{1-\cos(x)}{x^2}\to 0.5[/latex], pa [latex]\displaystyle\frac{(1-\cos(x))^2}{x^4}\to 0.25[/latex]. Kako [latex]\displaystyle\frac{\tan^2(x)}{x^2}\to 1[/latex], gotovi smo. :)
A što se tiče ovog drugog pitanja, ne znam baš definitivan odgovor, ali u svakom slučaju, vjerojatno je "dopustivije" tvrditi bez dokaza da [latex]\displaystyle\frac{\tan(x)}{x}\to 1[/latex] nego reći "ovo direktno slijedi iz 17. zadatka s vježbi kod asis. Gogića, samo uvrstimo [latex]a=2[/latex]". :D Eto, znam da nisam bio od neke pomoći. :)
Iznose  , ,  i i 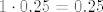 , ako se ne varam. Mislim, to ti zbilja nije teško izračunati, ne znam baš što predstavlja problem... , ako se ne varam. Mislim, to ti zbilja nije teško izračunati, ne znam baš što predstavlja problem...  Znaš da Znaš da 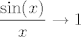 , pa i , pa i 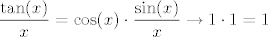 . Sad onda znaš i limese od . Sad onda znaš i limese od 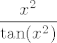 , , 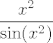 (primijeti da (primijeti da  , pa možeš formalno uvesti supstituciju , pa možeš formalno uvesti supstituciju 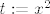 ). Za ovaj treći limes, znaš da ). Za ovaj treći limes, znaš da 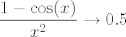 , pa , pa 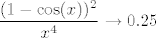 . Kako . Kako 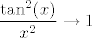 , gotovi smo. , gotovi smo. 
A što se tiče ovog drugog pitanja, ne znam baš definitivan odgovor, ali u svakom slučaju, vjerojatno je "dopustivije" tvrditi bez dokaza da 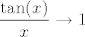 nego reći "ovo direktno slijedi iz 17. zadatka s vježbi kod asis. Gogića, samo uvrstimo nego reći "ovo direktno slijedi iz 17. zadatka s vježbi kod asis. Gogića, samo uvrstimo 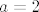 ". ".  Eto, znam da nisam bio od neke pomoći. Eto, znam da nisam bio od neke pomoći. 
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
|







