| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Cauchy
Forumaš(ica)
Pridružen/a: 29. 12. 2010. (10:50:16)
Postovi: (18)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 14:39 sri, 29. 12. 2010 Naslov: Postano: 14:39 sri, 29. 12. 2010 Naslov: |
    |
|
|
Evo kako bih ja to.
Odaberemo [latex]\epsilon> 0[/latex] po volji. Za njega želimo naći neki [latex]n_0 \in \mathbb{N}[/latex] takav da vrijedi [latex]| a^{\frac{1}{n}}-1 | < \epsilon [/latex] za sve [latex]n \geq n_0[/latex]. (to je definicija limesa)
za a=1 je tvrdnja trivijalna.
neka je a>1. Tada onu apsolutnu vrijednost možemo maknuti pa imamo:
[latex] a^{\frac{1}{n}}-1 < \epsilon [/latex] odnosno [latex] a^{\frac{1}{n}} < \epsilon +1 [/latex]
Želimo doći do n-a, pa cijelu nejednakost logaritmiramo (najljepše sa [latex]log_a[/latex] jer će nam onda onaj dio na lijevoj strani nestati, a znak nejednakosti se neće promijeniti jer je a>1 ). Ako logaritmiramo po bazi 10, onda ćemo dobiti ovo što si ti napisala.
Dobivamo:
[latex] \frac{1}{n} < log_a(\epsilon +1) [/latex] odnosno
[latex] n > \frac{1}{log_a(\epsilon +1)} [/latex]
(znak nejednakosti se neće promijeniti jer je ovaj log pozitivan)
Dakle [latex] a^{\frac{1}{n}}-1 < \epsilon [/latex] vrijedi čim je [latex] n > \frac{1}{log_a(\epsilon +1)} [/latex].
Pa uzmemo [latex]n_0 = \lfloor\frac{1}{log_a(\epsilon +1)} \rfloor +1[/latex]
pa ćemo imati da je za sve [latex]n \geq n_0[/latex] zadovoljeno [latex] a^{\frac{1}{n}}-1 < \epsilon [/latex] što daje da je 1 limes našeg niza.
Jako slično se radi za [latex]0<a<1[/latex], samo se treba paziti na predznake, i izraz unutar apsolutne vrijednosti se treba okrenuti. Probaj sama, pa ako neće ići pitaj :D
Evo kako bih ja to.
Odaberemo 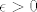 po volji. Za njega želimo naći neki po volji. Za njega želimo naći neki  takav da vrijedi takav da vrijedi 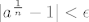 za sve za sve  . (to je definicija limesa) . (to je definicija limesa)
za a=1 je tvrdnja trivijalna.
neka je a>1. Tada onu apsolutnu vrijednost možemo maknuti pa imamo:
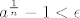 odnosno odnosno 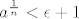
Želimo doći do n-a, pa cijelu nejednakost logaritmiramo (najljepše sa  jer će nam onda onaj dio na lijevoj strani nestati, a znak nejednakosti se neće promijeniti jer je a>1 ). Ako logaritmiramo po bazi 10, onda ćemo dobiti ovo što si ti napisala. jer će nam onda onaj dio na lijevoj strani nestati, a znak nejednakosti se neće promijeniti jer je a>1 ). Ako logaritmiramo po bazi 10, onda ćemo dobiti ovo što si ti napisala.
Dobivamo:
 odnosno odnosno
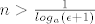
(znak nejednakosti se neće promijeniti jer je ovaj log pozitivan)
Dakle 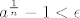 vrijedi čim je vrijedi čim je 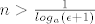 . .
Pa uzmemo 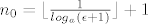
pa ćemo imati da je za sve  zadovoljeno zadovoljeno 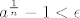 što daje da je 1 limes našeg niza. što daje da je 1 limes našeg niza.
Jako slično se radi za 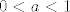 , samo se treba paziti na predznake, i izraz unutar apsolutne vrijednosti se treba okrenuti. Probaj sama, pa ako neće ići pitaj , samo se treba paziti na predznake, i izraz unutar apsolutne vrijednosti se treba okrenuti. Probaj sama, pa ako neće ići pitaj 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
Cauchy
Forumaš(ica)
Pridružen/a: 29. 12. 2010. (10:50:16)
Postovi: (18)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
Cauchy
Forumaš(ica)
Pridružen/a: 29. 12. 2010. (10:50:16)
Postovi: (18)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Cauchy
Forumaš(ica)
Pridružen/a: 29. 12. 2010. (10:50:16)
Postovi: (18)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Cauchy
Forumaš(ica)
Pridružen/a: 29. 12. 2010. (10:50:16)
Postovi: (18)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
Cauchy
Forumaš(ica)
Pridružen/a: 29. 12. 2010. (10:50:16)
Postovi: (18)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
Cauchy
Forumaš(ica)
Pridružen/a: 29. 12. 2010. (10:50:16)
Postovi: (18)16
|
|
| [Vrh] |
|
|













