| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 11:26 pet, 7. 1. 2011 Naslov: Postano: 11:26 pet, 7. 1. 2011 Naslov: |
    |
|
|
Ma nije to teoretski. :) Uglavnom, to se vjerojatno isto javljalo po forumu, ali da sad ne tražim...
Ima, naravno, hrpa primjera, mislim da sam se ja prvo sjetio nečega ogavnog što je sadržavalo [latex]\displaystyle\frac{1}{x}[/latex], ali vjerojatno je najjednostavniji kontraprimjer [latex]f(x)=\mathrm{sign}(x)[/latex], gdje je [latex]\mathrm{sign}[/latex] "funkcija predznaka" - za pozitivne [latex]x[/latex] je [latex]1[/latex], a za negativne [latex]-1[/latex] (da nam je nula u domeni, u njoj bi bila [latex]0[/latex]).
Funkcija očito nema limes u [latex]0[/latex] (zdesna je uvijek [latex]1[/latex], a slijeva [latex]-1[/latex]), a postoji limes od [latex]f(x^2)[/latex]. Naime, [latex]x^2>0[/latex], pa je u ovom slučaju vrijednost funkcije uvijek [latex]1[/latex]. Naravno, i sve druge grupe su potpuno iste i isti kontraprimjer vrijedi - poanta je da uvijek imamo uvjet da postoji limes od [latex]f(g(x))[/latex], gdje je [latex]g[/latex] neka funkcija veća od [latex]0[/latex].
Kažem, ovo je samo jedan od primjera - lako se vidi, mislim, da je nužni i dovoljni uvjet da funkcija bude kontraprimjer (za sve grupe) da ima limes u nuli zdesna, a da limes u nuli slijeva ili nema ili, ako ima, da on nije jednak limesu zdesna.
Ma nije to teoretski.  Uglavnom, to se vjerojatno isto javljalo po forumu, ali da sad ne tražim... Uglavnom, to se vjerojatno isto javljalo po forumu, ali da sad ne tražim...
Ima, naravno, hrpa primjera, mislim da sam se ja prvo sjetio nečega ogavnog što je sadržavalo 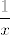 , ali vjerojatno je najjednostavniji kontraprimjer , ali vjerojatno je najjednostavniji kontraprimjer 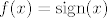 , gdje je , gdje je 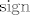 "funkcija predznaka" - za pozitivne "funkcija predznaka" - za pozitivne  je je  , a za negativne , a za negativne  (da nam je nula u domeni, u njoj bi bila (da nam je nula u domeni, u njoj bi bila  ). ).
Funkcija očito nema limes u  (zdesna je uvijek (zdesna je uvijek  , a slijeva , a slijeva  ), a postoji limes od ), a postoji limes od 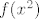 . Naime, . Naime, 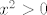 , pa je u ovom slučaju vrijednost funkcije uvijek , pa je u ovom slučaju vrijednost funkcije uvijek  . Naravno, i sve druge grupe su potpuno iste i isti kontraprimjer vrijedi - poanta je da uvijek imamo uvjet da postoji limes od . Naravno, i sve druge grupe su potpuno iste i isti kontraprimjer vrijedi - poanta je da uvijek imamo uvjet da postoji limes od 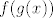 , gdje je , gdje je  neka funkcija veća od neka funkcija veća od  . .
Kažem, ovo je samo jedan od primjera - lako se vidi, mislim, da je nužni i dovoljni uvjet da funkcija bude kontraprimjer (za sve grupe) da ima limes u nuli zdesna, a da limes u nuli slijeva ili nema ili, ako ima, da on nije jednak limesu zdesna.
|
|
| [Vrh] |
|
zvonkec
Forumaš(ica)

Pridružen/a: 04. 11. 2010. (20:56:30)
Postovi: (37)16
Spol: 
|
|
| [Vrh] |
|
Togepi
Forumaš(ica)
Pridružen/a: 21. 11. 2010. (14:31:41)
Postovi: (2B)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 11:49 sub, 8. 1. 2011 Naslov: Postano: 11:49 sub, 8. 1. 2011 Naslov: |
    |
|
|
Nisi napisao/la o kojoj se grupi radi, a podosta su različite... no dobro, pretpostavljam da je u pitanju prva grupa jer se u trećoj ne radi o podjeli na "umnožak" skupova, a druga i četvrta ne bi trebale stvarati neke probleme s infimumima i supremumima (gledaj odvojeno parne i neparne [latex]m[/latex]).
E, a kod ove prve grupe radi se, u određenoj mjeri, o "zamci". Naime, niz od kojeg uzimamo najveće cijelo konvergira u dvije trećine, pa je sigurno da će nakon nekog (nadamo se kratkog) "vremena" svi članovi niza biti između [latex]0[/latex] i [latex]1[/latex]. Tada će to najveće cijelo biti [latex]0[/latex].
No dobro, pogledajmo kad je [latex]0\leq\displaystyle\frac{2n+3}{3n-8}<1[/latex]. Kao prvo, stavit ćemo uvjet da je [latex]n\geq 3[/latex] (jedinicu i dvojku lako provjerimo ručno). Dakle, ovo gore je u tom slučaju ekvivalentno s [latex]0\leq 2n+3<3n-8[/latex], tj. s [latex]n>11[/latex]. Dakle, sad znamo da će za sve [latex]n>11[/latex] najveće cijelo biti [latex]0[/latex].
Ove manje ili jednake [latex]11[/latex] možeš provjeriti i ručno, a možda je smisleno i ovako: dakle, računamo da (ako izuzmemo ovu prvu dvojicu, kad je nazivnik negativan), ako već ovaj razlomak nije manji od [latex]1[/latex], možda je za neke [latex]n[/latex] od [latex]3[/latex] do [latex]11[/latex] manji od [latex]2[/latex], a veći ili jednak [latex]1[/latex], pa mu opet znamo najveće cijelo. Pogledajmo: [latex]1\leq\displaystyle\frac{2n+3}{3n-8}<2[/latex] je ekvivalentno s [latex]n\leq 11[/latex] i [latex]n\geq 5[/latex].
I eto, sad smo manje-više gotovi: za [latex]n=1,2,3,4[/latex] ručno provjeri vrijednosti najvećeg cijelog (mislim da su [latex]-1[/latex], [latex]-4[/latex], [latex]9[/latex] i [latex]2[/latex], respektivno), a dalje se pojavljuju samo jedinice i nule. Stoga, supremum ovog skupa je najveći od spomenutih brojeva, [latex]9[/latex], a infimum najmanji: [latex]-4[/latex].
Eto, to je to. Nadam se da sam pogodio grupu. :)
(Naravno, u ovome gore, druga opcija koja ti se nudi je da uvidiš da je nakon trećeg člana ovaj pripadajući niz padajuć, a kako je najveće cijelo rastuća funkcija, tada je supremum ili u trećem članu ili u nekom od prve dvojice, a infimum ili u limesu za [latex]n\to +\infty[/latex] ili, ponovno, u nekom od prve dvojice. Tako ti je možda i lakše. :))
EDIT: Najveće cijelo nije neprekidna funkcija, naravno. :oops: Ispričavam se. Doduše, to ne mijenja ništa na ovom drugom ponuđenom rješenju - čak i kad bi išli tim putem, neprekidna je u [latex]2/3[/latex], gdje nam je bitno.
Nisi napisao/la o kojoj se grupi radi, a podosta su različite... no dobro, pretpostavljam da je u pitanju prva grupa jer se u trećoj ne radi o podjeli na "umnožak" skupova, a druga i četvrta ne bi trebale stvarati neke probleme s infimumima i supremumima (gledaj odvojeno parne i neparne  ). ).
E, a kod ove prve grupe radi se, u određenoj mjeri, o "zamci". Naime, niz od kojeg uzimamo najveće cijelo konvergira u dvije trećine, pa je sigurno da će nakon nekog (nadamo se kratkog) "vremena" svi članovi niza biti između  i i  . Tada će to najveće cijelo biti . Tada će to najveće cijelo biti  . .
No dobro, pogledajmo kad je 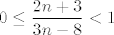 . Kao prvo, stavit ćemo uvjet da je . Kao prvo, stavit ćemo uvjet da je 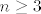 (jedinicu i dvojku lako provjerimo ručno). Dakle, ovo gore je u tom slučaju ekvivalentno s (jedinicu i dvojku lako provjerimo ručno). Dakle, ovo gore je u tom slučaju ekvivalentno s 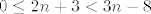 , tj. s , tj. s 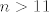 . Dakle, sad znamo da će za sve . Dakle, sad znamo da će za sve 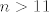 najveće cijelo biti najveće cijelo biti  . .
Ove manje ili jednake 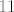 možeš provjeriti i ručno, a možda je smisleno i ovako: dakle, računamo da (ako izuzmemo ovu prvu dvojicu, kad je nazivnik negativan), ako već ovaj razlomak nije manji od možeš provjeriti i ručno, a možda je smisleno i ovako: dakle, računamo da (ako izuzmemo ovu prvu dvojicu, kad je nazivnik negativan), ako već ovaj razlomak nije manji od  , možda je za neke , možda je za neke  od od 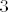 do do 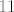 manji od manji od  , a veći ili jednak , a veći ili jednak  , pa mu opet znamo najveće cijelo. Pogledajmo: , pa mu opet znamo najveće cijelo. Pogledajmo: 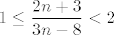 je ekvivalentno s je ekvivalentno s  i i 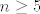 . .
I eto, sad smo manje-više gotovi: za 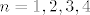 ručno provjeri vrijednosti najvećeg cijelog (mislim da su ručno provjeri vrijednosti najvećeg cijelog (mislim da su  , , 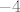 , ,  i i  , respektivno), a dalje se pojavljuju samo jedinice i nule. Stoga, supremum ovog skupa je najveći od spomenutih brojeva, , respektivno), a dalje se pojavljuju samo jedinice i nule. Stoga, supremum ovog skupa je najveći od spomenutih brojeva,  , a infimum najmanji: , a infimum najmanji: 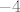 . .
Eto, to je to. Nadam se da sam pogodio grupu. 
(Naravno, u ovome gore, druga opcija koja ti se nudi je da uvidiš da je nakon trećeg člana ovaj pripadajući niz padajuć, a kako je najveće cijelo rastuća funkcija, tada je supremum ili u trećem članu ili u nekom od prve dvojice, a infimum ili u limesu za 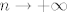 ili, ponovno, u nekom od prve dvojice. Tako ti je možda i lakše. ili, ponovno, u nekom od prve dvojice. Tako ti je možda i lakše.  ) )
EDIT: Najveće cijelo nije neprekidna funkcija, naravno.  Ispričavam se. Doduše, to ne mijenja ništa na ovom drugom ponuđenom rješenju - čak i kad bi išli tim putem, neprekidna je u Ispričavam se. Doduše, to ne mijenja ništa na ovom drugom ponuđenom rješenju - čak i kad bi išli tim putem, neprekidna je u 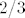 , gdje nam je bitno. , gdje nam je bitno.
Zadnja promjena: mornik; 11:58 sub, 8. 1. 2011; ukupno mijenjano 3 put/a.
|
|
| [Vrh] |
|
Togepi
Forumaš(ica)
Pridružen/a: 21. 11. 2010. (14:31:41)
Postovi: (2B)16
|
|
| [Vrh] |
|
Togepi
Forumaš(ica)
Pridružen/a: 21. 11. 2010. (14:31:41)
Postovi: (2B)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
 Postano: 17:04 sub, 8. 1. 2011 Naslov: Postano: 17:04 sub, 8. 1. 2011 Naslov: |
    |
|
|
Znaci ovako, posto su m,n pozitivni brojevi, izraz je takodjer strogo pozitivan, tako da ako imas neki izbor m,n (a imas) tako da postignes 0 od izraza, sigurno je to inf, jer ne postoji broj manji od 0, koji je pozitivan.
Znaci formalno je ovako: Neka je A=izraz. Zbog onog sto sam gore napisao je da je A>0. Sad n=1 i m->infinity, pa je lim A=0, stoga, dokazano.
Edit:
Drugi nacin bi bio ovakav.
0<A<epsilon (za neki fiksan epsilon) i za neke m>=m_0. Sada prema arhimedovom aksiomu postoji m_0 takav da je A<epsilon, za svaki epsilon, pa je prema teoremu o sendvicu limesA=0=infA
Znaci ovako, posto su m,n pozitivni brojevi, izraz je takodjer strogo pozitivan, tako da ako imas neki izbor m,n (a imas) tako da postignes 0 od izraza, sigurno je to inf, jer ne postoji broj manji od 0, koji je pozitivan.
Znaci formalno je ovako: Neka je A=izraz. Zbog onog sto sam gore napisao je da je A>0. Sad n=1 i m->infinity, pa je lim A=0, stoga, dokazano.
Edit:
Drugi nacin bi bio ovakav.
0<A<epsilon (za neki fiksan epsilon) i za neke m>=m_0. Sada prema arhimedovom aksiomu postoji m_0 takav da je A<epsilon, za svaki epsilon, pa je prema teoremu o sendvicu limesA=0=infA
|
|
| [Vrh] |
|
Buki
Forumaš(ica)

Pridružen/a: 17. 10. 2010. (20:15:17)
Postovi: (56)16
|
 Postano: 18:15 sub, 8. 1. 2011 Naslov: Postano: 18:15 sub, 8. 1. 2011 Naslov: |
    |
|
|
[quote="Tomislav"]Znaci ovako, posto su m,n pozitivni brojevi, izraz je takodjer strogo pozitivan, tako da ako imas neki izbor m,n (a imas) tako da postignes 0 od izraza, sigurno je to inf, jer ne postoji broj manji od 0, koji je pozitivan.
Znaci formalno je ovako: Neka je A=izraz. Zbog onog sto sam gore napisao je da je A>0. Sad n=1 i m->infinity, pa je lim A=0, stoga, dokazano.
Edit:
Drugi nacin bi bio ovakav.
0<A<epsilon (za neki fiksan epsilon) i za neke m>=m_0. Sada prema arhimedovom aksiomu postoji m_0 takav da je A<epsilon, za svaki epsilon, pa je prema teoremu o sendvicu limesA=0=infA[/quote]
vidio sam da se koristi finta da se kad je n=1 postize infinum, a kada je m=1 supremum,jel to dopusteno?
| Tomislav (napisa): | Znaci ovako, posto su m,n pozitivni brojevi, izraz je takodjer strogo pozitivan, tako da ako imas neki izbor m,n (a imas) tako da postignes 0 od izraza, sigurno je to inf, jer ne postoji broj manji od 0, koji je pozitivan.
Znaci formalno je ovako: Neka je A=izraz. Zbog onog sto sam gore napisao je da je A>0. Sad n=1 i m→infinity, pa je lim A=0, stoga, dokazano.
Edit:
Drugi nacin bi bio ovakav.
0<A<epsilon (za neki fiksan epsilon) i za neke m>=m_0. Sada prema arhimedovom aksiomu postoji m_0 takav da je A<epsilon, za svaki epsilon, pa je prema teoremu o sendvicu limesA=0=infA |
vidio sam da se koristi finta da se kad je n=1 postize infinum, a kada je m=1 supremum,jel to dopusteno?
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
zbunjena
Forumaš(ica)
Pridružen/a: 28. 06. 2010. (09:50:31)
Postovi: (14)16
Spol: 
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
|
| [Vrh] |
|
|








