| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Bruno^_^
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (20:22:27)
Postovi: (1D)16
|
 Postano: 20:52 čet, 13. 1. 2011 Naslov: Postano: 20:52 čet, 13. 1. 2011 Naslov: |
    |
|
|
Zapravo nije odgovoreno, dokazao sam da je <0,1> x <0,1> ekvipotentno s <0,1>, no da bi se dokazala tvdnja treba jos spomenuti (implicitnu) tvrdnju da je [0,1] ekvipotentno s <0,1> (koja u biti nije toliko implicitna ali se lako dokazuje).
Zapravo nije odgovoreno, dokazao sam da je <0,1> x <0,1> ekvipotentno s <0,1>, no da bi se dokazala tvdnja treba jos spomenuti (implicitnu) tvrdnju da je [0,1] ekvipotentno s <0,1> (koja u biti nije toliko implicitna ali se lako dokazuje).
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 20:58 čet, 13. 1. 2011 Naslov: Postano: 20:58 čet, 13. 1. 2011 Naslov: |
    |
|
|
[quote="Bruno^_^"]Zapravo nije odgovoreno, dokazao sam da je <0,1> x <0,1> ekvipotentno s <0,1>, no da bi se dokazala tvdnja treba jos spomenuti (implicitnu) tvrdnju da je [0,1] ekvipotentno s <0,1> (koja u biti nije toliko implicitna ali se lako dokazuje).[/quote]
Dokazao si da je [0,1]x[0,1] ekvipotentno sa [0,1]. Naime broj 0.999999999... koji je među ovim tvojim brojevima je zapravo jednak jedinici (geometrijski red).
Inače korisne stvari kod tih dokaza su da su svaka 2 intervala ekvipotentna (linearna fja) a <-pi/2,pi/2> je ekvipotentan sa R (tangens). S rubovima intervala isto nema problema, njih je lako zaobić :D
| Bruno^_^ (napisa): | | Zapravo nije odgovoreno, dokazao sam da je <0,1> x <0,1> ekvipotentno s <0,1>, no da bi se dokazala tvdnja treba jos spomenuti (implicitnu) tvrdnju da je [0,1] ekvipotentno s <0,1> (koja u biti nije toliko implicitna ali se lako dokazuje). |
Dokazao si da je [0,1]x[0,1] ekvipotentno sa [0,1]. Naime broj 0.999999999... koji je među ovim tvojim brojevima je zapravo jednak jedinici (geometrijski red).
Inače korisne stvari kod tih dokaza su da su svaka 2 intervala ekvipotentna (linearna fja) a ←pi/2,pi/2> je ekvipotentan sa R (tangens). S rubovima intervala isto nema problema, njih je lako zaobić 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
 Postano: 20:58 čet, 13. 1. 2011 Naslov: Postano: 20:58 čet, 13. 1. 2011 Naslov: |
    |
|
|
[quote="Phoenix"][quote="pedro"]može pomoć oko ovih zadataka:
[b]1)[/b] dokažite da su [0,1] x [0,1] i [0,1] ekvipotentni skupovi
[b]2)[/b] Konstruirajte surjekciju s Q u N.
[b]3)[/b] Konstruirajte surjekciju s R u Q.
nije mi baš jasno ni kak da započnem zadatak. hvala[/quote]
1) Već odgovoreno. :)
2) [latex]f(x)=|\left\lfloor x\right\rfloor|+1[/latex]
3) [latex]f(x)=g(x)*x[/latex]
[latex]g(x)[/latex] je Dirichletova funkcija. Znači, ako je [latex]x[/latex] iracionalan, [latex]f(x)=0[/latex]. U protivnom, [latex]f(x)=x[/latex], i to je tražena surjekcija.[/quote]
Hmm a kako bi onda npr f(x) moglo biti jednako -1/2?
Ako je x za kojeg ce f(x) biti -1/2 iracionalan, onda je g(x)*x=0, jer je g(x)=0.
Ako je x racionalan, onda je g(x)=x, pa je f(x)=x^2=-1/2..
Mozda g(x)=0 za iracionalne, a g(x)=1 za racionalne.. :wink: :idea:
| Phoenix (napisa): | | pedro (napisa): | može pomoć oko ovih zadataka:
1) dokažite da su [0,1] x [0,1] i [0,1] ekvipotentni skupovi
2) Konstruirajte surjekciju s Q u N.
3) Konstruirajte surjekciju s R u Q.
nije mi baš jasno ni kak da započnem zadatak. hvala |
1) Već odgovoreno. 
2) 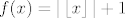
3) 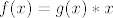
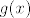 je Dirichletova funkcija. Znači, ako je je Dirichletova funkcija. Znači, ako je  iracionalan, iracionalan, 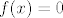 . U protivnom, . U protivnom, 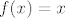 , i to je tražena surjekcija. , i to je tražena surjekcija. |
Hmm a kako bi onda npr f(x) moglo biti jednako -1/2?
Ako je x za kojeg ce f(x) biti -1/2 iracionalan, onda je g(x)*x=0, jer je g(x)=0.
Ako je x racionalan, onda je g(x)=x, pa je f(x)=x^2=-1/2..
Mozda g(x)=0 za iracionalne, a g(x)=1 za racionalne..  
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 21:22 čet, 13. 1. 2011 Naslov: Postano: 21:22 čet, 13. 1. 2011 Naslov: |
    |
|
|
Pa nije li to Pheonix napisao?!
Dirichletova funkcija je definirana na način da je 1 ako je x racionalan, a 0 ako je x iracionalan. ;)
Ako je [latex]x \in \mathbb{I}[/latex], onda je [latex]g(x) = 0[/latex], pa je [latex]f(x) = 0\cdot x = 0[/latex].
Ako je [latex]x \notin \mathbb{I}[/latex] (odnosno [latex]x \in \mathbb{Q}[/latex]), onda je [latex]g(x) = 1[/latex], pa je [latex]f(x) = 1 \cdot x = x[/latex].
Eto odgovora na pitanje kad će biti [latex]f(x) = -\frac{1}{2}[/latex]. To će biti kad je [latex]x = -\frac{1}{2}[/latex] (u tom je slučaju [latex]g(x) = 1[/latex] jer se radi o racionalnom broju).
Pa nije li to Pheonix napisao?!
Dirichletova funkcija je definirana na način da je 1 ako je x racionalan, a 0 ako je x iracionalan. 
Ako je 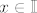 , onda je , onda je 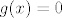 , pa je , pa je 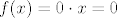 . .
Ako je 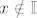 (odnosno (odnosno 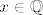 ), onda je ), onda je 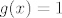 , pa je , pa je 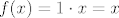 . .
Eto odgovora na pitanje kad će biti 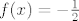 . To će biti kad je . To će biti kad je 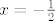 (u tom je slučaju (u tom je slučaju 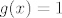 jer se radi o racionalnom broju). jer se radi o racionalnom broju).
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
|








