|
Ha dobro. Ugodnije je možda da pređem na limes funkcije - stvar je potpuno ista, ali ajde - ima više tabličnih limesa koji se time bave. Dakle, zanimat će nas [latex]\displaystyle\lim_{x\to +\infty} \sqrt{x}(x^{\frac{1}{x}}-1)=\lim_{x\to +\infty} \sqrt{x}(e^{\frac{\ln x}{x}}-1)[/latex]. Naravno, formalno, postojanje onog "tvog" limesa (za prirodne brojeve) ne garantira da će postojati ovaj tu limes, ali, ukoliko postoji limes ove funkcije (dakle, za sve realne brojeve), tada i onaj "tvoj" niz (koji se sastoji od vrijednosti funkcije za prirodne [latex]x[/latex]) konvergira prema istom limesu. To je intuitivno jasno, a nije teško ni za dokazati, reci ako treba pomoć. :)
E, sad, prije nego što odemo do kraja, samo jedna pomoćna tvrdnja. Za [latex]x\to +\infty[/latex] vrijedi [latex]\displaystyle\frac{\ln x}{x}\to 0[/latex]. Kako to dokazati (vidim da nema u tablici limesa): ovo čega sam se ja prvo sjetio i nije baš najljepše, ali ajde: dokazat ćemo da za dovoljno velike [latex]x[/latex] vrijedi [latex]0<\displaystyle\frac{\ln x}{x}<\frac{1}{\sqrt{x}}[/latex]. Lijeva strana je očita. Desna je ekvivalentna s [latex]\ln {x}<\sqrt{x}[/latex], tj. s [latex]x<e^{\sqrt{x}}[/latex]. A dobro, sad je dosta očito da to vrijedi, ali ako baš hoćemo biti formalni, neka je [latex]\lfloor\sqrt{x}\rfloor=t[/latex]. Tada je [latex]e^{\sqrt{x}}\geq e^t[/latex]. S druge strane, očito vrijedi [latex]x<(t+1)^2[/latex], a indukcijom lako pokažemo da za dovoljno velike prirodne [latex]t[/latex] vrijedi [latex]e^t>(t+1)^2[/latex]. Dakle, tvrdnja vrijedi za dovoljno velike [latex]x[/latex] - reci ako treba detaljnije raspisati.
No dobro, sad smo manje-više na kraju: [latex]\displaystyle\sqrt{x}(e^{\frac{\ln x}{x}}-1)=\sqrt{x}\frac{\ln{x}}{x}\frac{e^{\frac{\ln x}{x}}-1}{\frac{\ln{x}}{x}}[/latex]. Sad, kako znamo da razlomak s desne strane konvergira u [latex]1[/latex] (limes oblika [latex]\displaystyle\frac{e^t-1}{t}[/latex] za [latex]t\to 0[/latex]), a [latex]\displaystyle\sqrt{x}\frac{\ln{x}}{x}=2\frac{\ln{\sqrt{x}}}{\sqrt{x}}[/latex], pa i to, po gornjoj tvrdnji, konvergira u [latex]0[/latex], gotovi smo: limes je [latex]0\cdot 1=0[/latex].
Dakle, kao što sam gore objasnio, i limes pripadajućeg ("tvog") niza je [latex]0[/latex]. :)
Ha dobro. Ugodnije je možda da pređem na limes funkcije - stvar je potpuno ista, ali ajde - ima više tabličnih limesa koji se time bave. Dakle, zanimat će nas 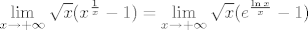 . Naravno, formalno, postojanje onog "tvog" limesa (za prirodne brojeve) ne garantira da će postojati ovaj tu limes, ali, ukoliko postoji limes ove funkcije (dakle, za sve realne brojeve), tada i onaj "tvoj" niz (koji se sastoji od vrijednosti funkcije za prirodne . Naravno, formalno, postojanje onog "tvog" limesa (za prirodne brojeve) ne garantira da će postojati ovaj tu limes, ali, ukoliko postoji limes ove funkcije (dakle, za sve realne brojeve), tada i onaj "tvoj" niz (koji se sastoji od vrijednosti funkcije za prirodne  ) konvergira prema istom limesu. To je intuitivno jasno, a nije teško ni za dokazati, reci ako treba pomoć. ) konvergira prema istom limesu. To je intuitivno jasno, a nije teško ni za dokazati, reci ako treba pomoć. 
E, sad, prije nego što odemo do kraja, samo jedna pomoćna tvrdnja. Za 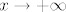 vrijedi vrijedi 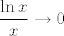 . Kako to dokazati (vidim da nema u tablici limesa): ovo čega sam se ja prvo sjetio i nije baš najljepše, ali ajde: dokazat ćemo da za dovoljno velike . Kako to dokazati (vidim da nema u tablici limesa): ovo čega sam se ja prvo sjetio i nije baš najljepše, ali ajde: dokazat ćemo da za dovoljno velike  vrijedi vrijedi 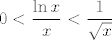 . Lijeva strana je očita. Desna je ekvivalentna s . Lijeva strana je očita. Desna je ekvivalentna s 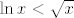 , tj. s , tj. s 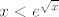 . A dobro, sad je dosta očito da to vrijedi, ali ako baš hoćemo biti formalni, neka je . A dobro, sad je dosta očito da to vrijedi, ali ako baš hoćemo biti formalni, neka je 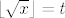 . Tada je . Tada je 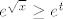 . S druge strane, očito vrijedi . S druge strane, očito vrijedi 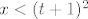 , a indukcijom lako pokažemo da za dovoljno velike prirodne , a indukcijom lako pokažemo da za dovoljno velike prirodne  vrijedi vrijedi 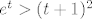 . Dakle, tvrdnja vrijedi za dovoljno velike . Dakle, tvrdnja vrijedi za dovoljno velike  - reci ako treba detaljnije raspisati. - reci ako treba detaljnije raspisati.
No dobro, sad smo manje-više na kraju: 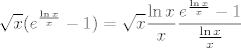 . Sad, kako znamo da razlomak s desne strane konvergira u . Sad, kako znamo da razlomak s desne strane konvergira u  (limes oblika (limes oblika 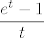 za za 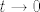 ), a ), a 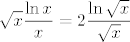 , pa i to, po gornjoj tvrdnji, konvergira u , pa i to, po gornjoj tvrdnji, konvergira u  , gotovi smo: limes je , gotovi smo: limes je 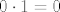 . .
Dakle, kao što sam gore objasnio, i limes pripadajućeg ("tvog") niza je  . . 
|






