| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Bug
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: 
Lokacija: Kako kad!!
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 16:49 pon, 17. 1. 2011 Naslov: Postano: 16:49 pon, 17. 1. 2011 Naslov: |
    |
|
|
ako se ne varam, a reko bih da se ne varam
f(lambda) = 1, f'(lambda) = 0
f(A) = f(0)p1+f'(0)p2 => I = 1p1+0p2 odakle je p1=I
f(lambda)=lambda, f'(lambda)=1
f(A)= f(0)p1+f'(0)p2= 0p1+1p2 odakle je p2=A
pa onda dalje ide ovo što piše
ako se ne varam, a reko bih da se ne varam
f(lambda) = 1, f'(lambda) = 0
f(A) = f(0)p1+f'(0)p2 => I = 1p1+0p2 odakle je p1=I
f(lambda)=lambda, f'(lambda)=1
f(A)= f(0)p1+f'(0)p2= 0p1+1p2 odakle je p2=A
pa onda dalje ide ovo što piše
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
Bug
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: 
Lokacija: Kako kad!!
|
 Postano: 16:59 pon, 17. 1. 2011 Naslov: Postano: 16:59 pon, 17. 1. 2011 Naslov: |
    |
|
|
[quote="Milojko"]ako se ne varam, a reko bih da se ne varam
f(lambda) = 1, f'(lambda) = 0
f(A) = f(0)p1+f'(0)p2 => I = 1p1+0p2 odakle je p1=I[/quote]
kako znam da je f(0) = 1
sta to vrijedi za bilo koji labmda pa tako i specijalno za 0
[quote="Milojko"]
f(lambda)=lambda, f'(lambda)=1
f(A)= f(0)p1+f'(0)p2= 0p1+1p2 odakle je p2=A
pa onda dalje ide ovo što piše[/quote]
zasto je ovdje f(0)=0...
aha ovdje ako sam skuzio vrijedi isto f(1)=1, f(2)=2....a za svaki izbor lambde, derivacija f-je u lambdi je 1? ili se varam?
| Milojko (napisa): | ako se ne varam, a reko bih da se ne varam
f(lambda) = 1, f'(lambda) = 0
f(A) = f(0)p1+f'(0)p2 ⇒ I = 1p1+0p2 odakle je p1=I |
kako znam da je f(0) = 1
sta to vrijedi za bilo koji labmda pa tako i specijalno za 0
| Milojko (napisa): |
f(lambda)=lambda, f'(lambda)=1
f(A)= f(0)p1+f'(0)p2= 0p1+1p2 odakle je p2=A
pa onda dalje ide ovo što piše |
zasto je ovdje f(0)=0...
aha ovdje ako sam skuzio vrijedi isto f(1)=1, f(2)=2....a za svaki izbor lambde, derivacija f-je u lambdi je 1? ili se varam?
_________________
Everybody Dies...
Nobody is perfect...
Non scholae, sed vitae discimus
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 17:04 pon, 17. 1. 2011 Naslov: Postano: 17:04 pon, 17. 1. 2011 Naslov: |
    |
|
|
kolko je f(0) ako je f(x) = 1?
kolka je onda derivacija?
a ako je f(x) = x, što je onda f(0)? a f'?
uvrštavaš te proizvoljne funkcije, obično oćeš poništit neke faktore uz neki p tka da ti je lakše za računat
kolko je f(0) ako je f(x) = 1?
kolka je onda derivacija?
a ako je f(x) = x, što je onda f(0)? a f'?
uvrštavaš te proizvoljne funkcije, obično oćeš poništit neke faktore uz neki p tka da ti je lakše za računat
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
Bug
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: 
Lokacija: Kako kad!!
|
|
| [Vrh] |
|
Bug
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: 
Lokacija: Kako kad!!
|
 Postano: 20:51 pon, 17. 1. 2011 Naslov: Postano: 20:51 pon, 17. 1. 2011 Naslov: |
    |
|
|
Evo ovakav je sad moj problem
[latex]f(A) = cos (2A^ 5) + cos (A^3)[/latex]
[latex]p_1= A, p_2=A-2I, p_3=1/2A^2-4A+4I[/latex]
[latex]minimalni=(2-\lambda)^2[/latex]
[latex]f(A)=f(2)p_1+f'(2)p_2+f''(2)p_3[/latex]
sad se jeli 2 uvrsti u [latex]f(A)[/latex], pa u [latex]f'(A)[/latex], pa u [latex]f''(A)[/latex]? Da dobijem brojeve...
Meni to nekak kobasicasto izgleda... jel netko rijesio 4. zadatak s kolokvija s prosle godine, da usporedimo rezultate
edit: ne zamjerite, ne znam pisat u latexu, ali se ipak ovako malo bolje vidi :)
Evo ovakav je sad moj problem
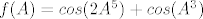
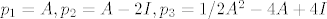
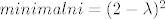
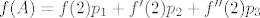
sad se jeli 2 uvrsti u 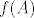 , pa u , pa u 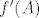 , pa u , pa u 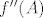 ? Da dobijem brojeve... ? Da dobijem brojeve...
Meni to nekak kobasicasto izgleda... jel netko rijesio 4. zadatak s kolokvija s prosle godine, da usporedimo rezultate
edit: ne zamjerite, ne znam pisat u latexu, ali se ipak ovako malo bolje vidi 
_________________
Everybody Dies...
Nobody is perfect...
Non scholae, sed vitae discimus
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 0:10 uto, 18. 1. 2011 Naslov: Postano: 0:10 uto, 18. 1. 2011 Naslov: |
    |
|
|
pa kad si dodo i ovu drugu derivaciju
imaš dvicu kao duplu nultočku minimalnog polinoma pa je oblik svake funkcije od A jednak
f(A)=f(2)p_1+f'(2)p_2
pa kad si dodo i ovu drugu derivaciju
imaš dvicu kao duplu nultočku minimalnog polinoma pa je oblik svake funkcije od A jednak
f(A)=f(2)p_1+f'(2)p_2
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
|












