| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
654321
Forumaš(ica)

Pridružen/a: 18. 01. 2011. (18:30:01)
Postovi: (D)16
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
 Postano: 12:29 sub, 22. 1. 2011 Naslov: Postano: 12:29 sub, 22. 1. 2011 Naslov: |
    |
|
|
Znaci pod a) nas zanima za koje x je funkcija definirana....
imamo samo korijen tako da x mora biti [0, +beskonacno>
Za b) i c) dio bilo bi najbolje funkciju rastaviti na kompoziciju funkcija...
[latex]f(x)=x-8\sqrt[2]{x}+12[/latex]
Rastavimo na [latex]g(x)=x^{2}-8x+12[/latex] i [latex]h(x)=\sqrt[2]{x}
[/latex]
b). trazimo f(x)=(<0,25>) => g(h(<0,25>)
i). gledamo prvo funkciju h(x), ona strogo raste za [0,+besk> pa nam je
h(<0,25>)=<0,5>
ii). gledamo funkciju g(x)= <0,5> vidimo da je to kvadratna funkcija sa nultockama 2,6... i otvorena je prema gore stoga nam je tu najmanja vrijednost tjeme funkcije (4,-4) a najveca iz intervala <0,5> za nulu i iznosi 12... Dakle f(<0,25>)=[-4,12>
c). Idemo obrnutim redosljedom nego u b) pa imamo
pa je [latex]f(<-3,0>)^{-1}=h^{-1} * [g^{-1}(<-3,0>)][/latex]
vidimo da kvadratna funkcija na tom intervalu <-3,0> pada pa je
[latex]-3<g^{-1}(<-3,0>)<0[/latex] i onda jos za h(x)^{-1} od intervala kojeg dobijes...
Nadam se da nisam nigdje pogrijesio... :)
Znaci pod a) nas zanima za koje x je funkcija definirana....
imamo samo korijen tako da x mora biti [0, +beskonacno>
Za b) i c) dio bilo bi najbolje funkciju rastaviti na kompoziciju funkcija...
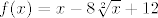
Rastavimo na 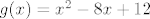 i i 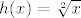
b). trazimo f(x)=(<0,25>) ⇒ g(h(<0,25>)
i). gledamo prvo funkciju h(x), ona strogo raste za [0,+besk> pa nam je
h(<0,25>)=<0,5>
ii). gledamo funkciju g(x)= <0,5> vidimo da je to kvadratna funkcija sa nultockama 2,6... i otvorena je prema gore stoga nam je tu najmanja vrijednost tjeme funkcije (4,-4) a najveca iz intervala <0,5> za nulu i iznosi 12... Dakle f(<0,25>)=[-4,12>
c). Idemo obrnutim redosljedom nego u b) pa imamo
pa je 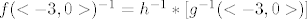
vidimo da kvadratna funkcija na tom intervalu ←3,0> pada pa je
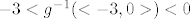 i onda jos za h(x)^{-1} od intervala kojeg dobijes... i onda jos za h(x)^{-1} od intervala kojeg dobijes...
Nadam se da nisam nigdje pogrijesio... 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 14:25 sub, 22. 1. 2011 Naslov: Postano: 14:25 sub, 22. 1. 2011 Naslov: |
    |
|
|
Ova praslika mi nije posve jasna,
ja sam ovako zapisala: f^-1 (<-3,0>)=(g_1)^-1 o (g_2)^-1(<-3,0>)=
(g_1)^-1 ( <2,3> U <5, 6> ) = <4, 9> U <25, 36>,
da li je to ispravan nacin.
Ili treba uvijek ici po definiciji praslike i rjesavat one dvije nejednadzbe.
g_1 = korjen(x)
g_2 = kvadratna
Ova praslika mi nije posve jasna,
ja sam ovako zapisala: f^-1 (<-3,0>)=(g_1)^-1 o (g_2)^-1(<-3,0>)=
(g_1)^-1 ( <2,3> U <5, 6> ) = <4, 9> U <25, 36>,
da li je to ispravan nacin.
Ili treba uvijek ici po definiciji praslike i rjesavat one dvije nejednadzbe.
g_1 = korjen(x)
g_2 = kvadratna
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
654321
Forumaš(ica)

Pridružen/a: 18. 01. 2011. (18:30:01)
Postovi: (D)16
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
654321
Forumaš(ica)

Pridružen/a: 18. 01. 2011. (18:30:01)
Postovi: (D)16
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
chiko
Forumaš(ica)


Pridružen/a: 14. 09. 2010. (17:43:27)
Postovi: (E)16
Spol: 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 17:50 ned, 23. 1. 2011 Naslov: Postano: 17:50 ned, 23. 1. 2011 Naslov: |
    |
|
|
Znaci prvo provjer par elemenata tog niza i utvrdi dal i je rastuci ili padajuci, odnoso od kojeg je elementa strogo padajuci odnosno rastuci (jer se moze desiti da prva dva, tri ... elementa budu izmjenicno, jedan veci drugi manji, pa onda ustvrdis da od jednog elementa niz je padaj ili rast.), no u oovm slucaju nakon prva tri elemnta vidimo da je niz rastuci, znaci:
a_1 = 1 (to vec imamo)
a_2=2
a_3=4 ... (te brojeve dobivamo tako da uvrstavamo n-ove )
----> Tvrdimo da je niz rastuci, a_n < a_n+1
DOKAZ: (indukcija)
BAZA: 1<2 (vrijedi)
PRETPOSTAVKA: Pretpostavimo da tvrdnja vrijedi za neki n iz N
KORAK: (provjeravamo za sljedeca dva clana da li su u istom odnosu)
a_n+1 < a_n+2
2^(a_n) < 2^(a_n+1) ----> prema pretpostsavci znamo da je
a_n<a_n+1
pa onda ta nejednakost vrijedi
-----> (sa strane si izracunao limes tog niza i uvidio da se potencija povecava, tako i broj ide u beskonacnost pa limes tog niza ne postoji jer nije omeđen odozgo, niz divergira)
Znaci: limes ne postoji.
Ja se nadam da je to dobro.
[size=9][color=#999999]Added after 3 minutes:[/color][/size]
[quote="Tomislav"]Ma zar je tako jako uzasno tesko pogledati zadnja 2-3 topica koji su jos uvijek aktivni, da SLUCAJNO mozda nisu ti ISTI zadaci vec rijeseni? Cisto da dodam imas link odmah iznad svog posta gdje ti je rjesenje... :shock: :?
Edit: Vidim da jos uvijek postoje "genijalci" koji mi za ovakve postove vole davati osude, umjesto da budu zahvalni sto im netko rjesava te zadacice.. mislim stvarno ste katastrofa.[/quote]
Rijec je o 2.zadatku iz 2009 ako se ja ne varam, a taj sigurno nismo rjesili na netu. Nemojte jedni drugima zamjerati, svima nam je ista briga, a to je matematika, zato postujte svecije pitanje, ako zelis odgovori, a ako ne, nemoj opet na takav nacin odoggovarati, nekome ce mozda to ozalostiti dan, meni recimo sigurno bi, da sam zatrazila pomoc,a dobila takav odogovor, zato mislim da bi mozda mogao jos nekoga. Lijep i na blag nacin komunicirajmo bez obzira da li netko pitao jednu stvar 100 puta.
Znaci prvo provjer par elemenata tog niza i utvrdi dal i je rastuci ili padajuci, odnoso od kojeg je elementa strogo padajuci odnosno rastuci (jer se moze desiti da prva dva, tri ... elementa budu izmjenicno, jedan veci drugi manji, pa onda ustvrdis da od jednog elementa niz je padaj ili rast.), no u oovm slucaju nakon prva tri elemnta vidimo da je niz rastuci, znaci:
a_1 = 1 (to vec imamo)
a_2=2
a_3=4 ... (te brojeve dobivamo tako da uvrstavamo n-ove )
----> Tvrdimo da je niz rastuci, a_n < a_n+1
DOKAZ: (indukcija)
BAZA: 1<2 (vrijedi)
PRETPOSTAVKA: Pretpostavimo da tvrdnja vrijedi za neki n iz N
KORAK: (provjeravamo za sljedeca dva clana da li su u istom odnosu)
a_n+1 < a_n+2
2^(a_n) < 2^(a_n+1) ----> prema pretpostsavci znamo da je
a_n<a_n+1
pa onda ta nejednakost vrijedi
-----> (sa strane si izracunao limes tog niza i uvidio da se potencija povecava, tako i broj ide u beskonacnost pa limes tog niza ne postoji jer nije omeđen odozgo, niz divergira)
Znaci: limes ne postoji.
Ja se nadam da je to dobro.
Added after 3 minutes:
| Tomislav (napisa): | Ma zar je tako jako uzasno tesko pogledati zadnja 2-3 topica koji su jos uvijek aktivni, da SLUCAJNO mozda nisu ti ISTI zadaci vec rijeseni? Cisto da dodam imas link odmah iznad svog posta gdje ti je rjesenje...  
Edit: Vidim da jos uvijek postoje "genijalci" koji mi za ovakve postove vole davati osude, umjesto da budu zahvalni sto im netko rjesava te zadacice.. mislim stvarno ste katastrofa. |
Rijec je o 2.zadatku iz 2009 ako se ja ne varam, a taj sigurno nismo rjesili na netu. Nemojte jedni drugima zamjerati, svima nam je ista briga, a to je matematika, zato postujte svecije pitanje, ako zelis odgovori, a ako ne, nemoj opet na takav nacin odoggovarati, nekome ce mozda to ozalostiti dan, meni recimo sigurno bi, da sam zatrazila pomoc,a dobila takav odogovor, zato mislim da bi mozda mogao jos nekoga. Lijep i na blag nacin komunicirajmo bez obzira da li netko pitao jednu stvar 100 puta.
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 18:06 ned, 23. 1. 2011 Naslov: Postano: 18:06 ned, 23. 1. 2011 Naslov: |
    |
|
|
[quote="Tomislav"]Mozes li molim te copy/paste link koji je chiko dao, te pogledati koji je 2. zadatak, tj. 2. zadatak pod a)? Meni se cini da je on identican onom koji sam ja rijesio u topicu kojeg sam linkao. A kao sto rekoh, topic je aktivan i moj post je 2. po redu, tako da vjerujem da bi se rjesenje naslo brze nego sto je trebalo da se napise pitanje da ga se rijesi i posta isto.[/quote]
Dobro, u pravu si. Covjek je spregledao, sta ces, nije kraj svijeta. :wink:
| Tomislav (napisa): | | Mozes li molim te copy/paste link koji je chiko dao, te pogledati koji je 2. zadatak, tj. 2. zadatak pod a)? Meni se cini da je on identican onom koji sam ja rijesio u topicu kojeg sam linkao. A kao sto rekoh, topic je aktivan i moj post je 2. po redu, tako da vjerujem da bi se rjesenje naslo brze nego sto je trebalo da se napise pitanje da ga se rijesi i posta isto. |
Dobro, u pravu si. Covjek je spregledao, sta ces, nije kraj svijeta. 
|
|
| [Vrh] |
|
chiko
Forumaš(ica)


Pridružen/a: 14. 09. 2010. (17:43:27)
Postovi: (E)16
Spol: 
|
|
| [Vrh] |
|
sstudentica
Forumaš(ica)
Pridružen/a: 30. 11. 2010. (13:18:02)
Postovi: (3A)16
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
|









