| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
klopka
Forumaš(ica)
Pridružen/a: 20. 01. 2011. (10:10:02)
Postovi: (1B)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 15:04 ned, 23. 1. 2011 Naslov: Postano: 15:04 ned, 23. 1. 2011 Naslov: |
    |
|
|
Ma, samo raspiši [latex]\displaystyle\frac{\sinh x}{x}[/latex] kao [latex]\displaystyle\frac{1}{2}\frac{e^x-e^{-x}}{x}=\frac{1}{2}(\frac{e^x-1}{x}+\frac{e^{-x}-1}{-x})[/latex]. Ove limese sad znaš odrediti. :) A što se tiče toga jel treba to dokazivati u kolokvijima, koliko vidim, stvar je u službenim formulama, pa pretpostavljam da se može koristiti kao poznata činjenica.
A, Phoenix je bio brži. :D
Ma, samo raspiši  kao kao 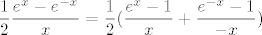 . Ove limese sad znaš odrediti. . Ove limese sad znaš odrediti.  A što se tiče toga jel treba to dokazivati u kolokvijima, koliko vidim, stvar je u službenim formulama, pa pretpostavljam da se može koristiti kao poznata činjenica. A što se tiče toga jel treba to dokazivati u kolokvijima, koliko vidim, stvar je u službenim formulama, pa pretpostavljam da se može koristiti kao poznata činjenica.
A, Phoenix je bio brži. 
|
|
| [Vrh] |
|
vuja
Forumaš(ica)


Pridružen/a: 26. 09. 2009. (12:57:07)
Postovi: (2C)16
Spol: 
|
|
| [Vrh] |
|
lalala5
Forumaš(ica)

Pridružen/a: 06. 10. 2010. (17:54:28)
Postovi: (3C)16
|
|
| [Vrh] |
|
vuja
Forumaš(ica)


Pridružen/a: 26. 09. 2009. (12:57:07)
Postovi: (2C)16
Spol: 
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 15:32 ned, 23. 1. 2011 Naslov: Postano: 15:32 ned, 23. 1. 2011 Naslov: |
    |
|
|
LaTeXu se ne sviđa kakav znak koristiš za minus. :D
Dakle, zadan je ovaj skup: [latex]S := \left\{ \frac{12m+ n-3mn+7}{5m-2n-2mn+5} : m,n \in \mathbb{N} \right\}[/latex].
Što radimo? Prvo uočavamo da se nazivnik može faktorizirati na sljedeći način: [latex](m+1)(5-2n)[/latex]. Sada bih volio nekako "oblikovati" brojnik tako da cjelokupni razlomak mogu rastaviti posebno na dva razlomka, pri čemu se u svakom od njih pojavljuje samo jedna varijabla. Tada mogu dalje koristiti formulu za "zbroj skupova" i onda se bavimo "sa svakim razlomkom posebno" (odnosno, sa svakim skupom posebno).
Dakle, želim dobiti ovakav rastav: [latex]\frac{(m+1)(An+B)}{(m+1)(5-2n)} +\frac{(5-2n)(Cm+D)}{(m+1)(5-2n)}[/latex]. Kada bih znao vrijednosti za [latex]A[/latex], [latex]B[/latex], [latex]C[/latex] i [latex]D[/latex], onda bih samo promatrao razlomke kada mi se zajednički faktori u brojniku i nazivniku "pokrate".
Sada samo zbrojiš ta dva razlomka i onda brojnik koji dobiješ izjednačiš s izrazom [latex]12m+ n-3mn+7[/latex]. Preostalo ti prepuštam za vježbu. :)
P. S. Ako slučajno dobiješ parametarska rješenja za ova 4 koeficijenta, bez brige - samo uvrsti proizvoljan broj za svaki parametar i onda izračunaj sva četiri koeficijenta. Infimumi i supremumi dva skupa koje promatraš mogu varirati, ali konačno rješenje će opet biti isto. :D
LaTeXu se ne sviđa kakav znak koristiš za minus. 
Dakle, zadan je ovaj skup: 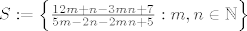 . .
Što radimo? Prvo uočavamo da se nazivnik može faktorizirati na sljedeći način: 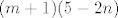 . Sada bih volio nekako "oblikovati" brojnik tako da cjelokupni razlomak mogu rastaviti posebno na dva razlomka, pri čemu se u svakom od njih pojavljuje samo jedna varijabla. Tada mogu dalje koristiti formulu za "zbroj skupova" i onda se bavimo "sa svakim razlomkom posebno" (odnosno, sa svakim skupom posebno). . Sada bih volio nekako "oblikovati" brojnik tako da cjelokupni razlomak mogu rastaviti posebno na dva razlomka, pri čemu se u svakom od njih pojavljuje samo jedna varijabla. Tada mogu dalje koristiti formulu za "zbroj skupova" i onda se bavimo "sa svakim razlomkom posebno" (odnosno, sa svakim skupom posebno).
Dakle, želim dobiti ovakav rastav: 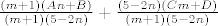 . Kada bih znao vrijednosti za . Kada bih znao vrijednosti za  , ,  , ,  i i 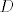 , onda bih samo promatrao razlomke kada mi se zajednički faktori u brojniku i nazivniku "pokrate". , onda bih samo promatrao razlomke kada mi se zajednički faktori u brojniku i nazivniku "pokrate".
Sada samo zbrojiš ta dva razlomka i onda brojnik koji dobiješ izjednačiš s izrazom  . Preostalo ti prepuštam za vježbu. . Preostalo ti prepuštam za vježbu. 
P. S. Ako slučajno dobiješ parametarska rješenja za ova 4 koeficijenta, bez brige - samo uvrsti proizvoljan broj za svaki parametar i onda izračunaj sva četiri koeficijenta. Infimumi i supremumi dva skupa koje promatraš mogu varirati, ali konačno rješenje će opet biti isto. 
|
|
| [Vrh] |
|
vuja
Forumaš(ica)


Pridružen/a: 26. 09. 2009. (12:57:07)
Postovi: (2C)16
Spol: 
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 16:56 ned, 23. 1. 2011 Naslov: Postano: 16:56 ned, 23. 1. 2011 Naslov: |
    |
|
|
2008.
2. b) Stvar je izrazito trivijalna (ali možda malo teže za uočiti ako nisi uvježban) - teorem o sendviču! :D
Naime, vrijedi [latex]-1 \leq sin(n^2e^n) \leq 1[/latex], za bilo koji [latex]n[/latex]. Podijeliš li sve ovo s [latex]n^2[/latex], dobit ćeš početni izraz ograničen s dvama izrazima koji konvergiraju u 0. Primijeniš teorem o sendviču i to je to.
4. a) U brojniku izluči [latex]e^{sin(x)}[/latex], a u nazivniku izluči [latex]e^x[/latex]. Ovo što smo izlučili nam ne smeta jer su oba izraza kao funkcije neprekidni u 0 i jednaki su 1. Ono što je ostalo u brojniku i nazivniku središ tako da brojnik dijeliš s [latex]sin(2x)-sin(x)[/latex], a nazivnik s [latex]x[/latex] (zato što imaš poznati limes s [latex]e^x[/latex]. Preostaje ti još razlomak [latex]\frac{sin(2x)-sin(x)}{x}[/latex]. Ali limes ovoga znamo jer je [latex]\frac{sin(2x)-sin(x)}{x}=\frac{sin(2x)}{x}-\frac{sin(x)}{x}=2\frac{sin(2x)}{2x}-\frac{sin(x)}{x}[/latex].
b) Racionaliziraj i brojnik i nazivnik. Nakon što ti se brojnik i nazivnik "pokrate", uvstiš [latex]x=6[/latex] (jer je izraz koji dobiješ neprekidan u toj točki) i imaš rješenje.
2010.
4. a) Nakon što racionaliziraš nazivnik, iskoristit ćeš formulu za limes s [latex]e^x[/latex] i za limes s [latex]ch(x)[/latex] tako što ćeš podijeliti brojnik i nazivnik s odgovarajućim izrazima. Rješenje slijedi odmah nakon tog koraka.
Eto! Nadam se da nisam bio presažet s ovim naputcima. Treba li još nešto objasniti, reci. :)
2008.
2. b) Stvar je izrazito trivijalna (ali možda malo teže za uočiti ako nisi uvježban) - teorem o sendviču! 
Naime, vrijedi  , za bilo koji , za bilo koji  . Podijeliš li sve ovo s . Podijeliš li sve ovo s 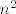 , dobit ćeš početni izraz ograničen s dvama izrazima koji konvergiraju u 0. Primijeniš teorem o sendviču i to je to. , dobit ćeš početni izraz ograničen s dvama izrazima koji konvergiraju u 0. Primijeniš teorem o sendviču i to je to.
4. a) U brojniku izluči 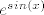 , a u nazivniku izluči , a u nazivniku izluči 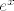 . Ovo što smo izlučili nam ne smeta jer su oba izraza kao funkcije neprekidni u 0 i jednaki su 1. Ono što je ostalo u brojniku i nazivniku središ tako da brojnik dijeliš s . Ovo što smo izlučili nam ne smeta jer su oba izraza kao funkcije neprekidni u 0 i jednaki su 1. Ono što je ostalo u brojniku i nazivniku središ tako da brojnik dijeliš s 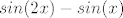 , a nazivnik s , a nazivnik s  (zato što imaš poznati limes s (zato što imaš poznati limes s 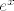 . Preostaje ti još razlomak . Preostaje ti još razlomak 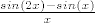 . Ali limes ovoga znamo jer je . Ali limes ovoga znamo jer je 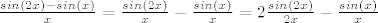 . .
b) Racionaliziraj i brojnik i nazivnik. Nakon što ti se brojnik i nazivnik "pokrate", uvstiš 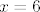 (jer je izraz koji dobiješ neprekidan u toj točki) i imaš rješenje. (jer je izraz koji dobiješ neprekidan u toj točki) i imaš rješenje.
2010.
4. a) Nakon što racionaliziraš nazivnik, iskoristit ćeš formulu za limes s 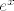 i za limes s i za limes s 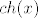 tako što ćeš podijeliti brojnik i nazivnik s odgovarajućim izrazima. Rješenje slijedi odmah nakon tog koraka. tako što ćeš podijeliti brojnik i nazivnik s odgovarajućim izrazima. Rješenje slijedi odmah nakon tog koraka.
Eto! Nadam se da nisam bio presažet s ovim naputcima. Treba li još nešto objasniti, reci. 
|
|
| [Vrh] |
|
vuja
Forumaš(ica)


Pridružen/a: 26. 09. 2009. (12:57:07)
Postovi: (2C)16
Spol: 
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 19:24 ned, 23. 1. 2011 Naslov: Postano: 19:24 ned, 23. 1. 2011 Naslov: |
    |
|
|
Moze provjera zadataka s popravnog kolokvija 2007,
http://web.math.hr/nastava/analiza/kol/ma1-0708-kp.pdf
1. zad: nema ga :S :S
2.zad: a)niz je padajuci, omeđen odozdo s 3, limes je 3.
b) (valjda tu treba samo obicni limes izracunati??) -1/5
3.zad: a) f^-1( <-3, 0] )= [ln2, ln3> U <ln5, ln6]
b) f ( [0, ln5>)= [-4, 5]
4.zad: supS= 11/3=maxS
infS= 1=minS
5.zad: a) 1/2
b) 1/ korjen(e)
2008. (popravni) :
Zamolila bih za objasnjenje prvog i 3. zadatka molim vas. Hvala. :oops:
[size=9][color=#999999]Added after 38 minutes:[/color][/size]
[quote="frutabella"]Moze provjera zadataka s popravnog kolokvija 2007,
http://web.math.hr/nastava/analiza/kol/ma1-0708-kp.pdf
1. zad: nema ga :S :S
2.zad: a)niz je padajuci, omeđen odozdo s 3, limes je 3.
b) (valjda tu treba samo obicni limes izracunati??) -1/5
3.zad: a) f^-1( <-3, 0] )= [ln2, ln3> U <ln5, ln6]
b) f ( [0, ln5>)= [-4, 5]
4.zad: supS= 11/3=maxS
infS= 1=minS
5.zad: a) 1/2
b) 1/ korjen(e)
2008. (popravni) :
Zamolila bih za objasnjenje prvog i 3. zadatka molim vas. Hvala. :oops:[/quote]
2008. pod 3.b) rjesih, dobila sam [ -11/4, 1 >, a ne znam kako da pod a)
Moze provjera zadataka s popravnog kolokvija 2007,
http://web.math.hr/nastava/analiza/kol/ma1-0708-kp.pdf
1. zad: nema ga :S :S
2.zad: a)niz je padajuci, omeđen odozdo s 3, limes je 3.
b) (valjda tu treba samo obicni limes izracunati??) -1/5
3.zad: a) f^-1( ←3, 0] )= [ln2, ln3> U <ln5, ln6]
b) f ( [0, ln5>)= [-4, 5]
4.zad: supS= 11/3=maxS
infS= 1=minS
5.zad: a) 1/2
b) 1/ korjen(e)
2008. (popravni) :
Zamolila bih za objasnjenje prvog i 3. zadatka molim vas. Hvala. 
Added after 38 minutes:
| frutabella (napisa): | Moze provjera zadataka s popravnog kolokvija 2007,
http://web.math.hr/nastava/analiza/kol/ma1-0708-kp.pdf
1. zad: nema ga :S :S
2.zad: a)niz je padajuci, omeđen odozdo s 3, limes je 3.
b) (valjda tu treba samo obicni limes izracunati??) -1/5
3.zad: a) f^-1( ←3, 0] )= [ln2, ln3> U <ln5, ln6]
b) f ( [0, ln5>)= [-4, 5]
4.zad: supS= 11/3=maxS
infS= 1=minS
5.zad: a) 1/2
b) 1/ korjen(e)
2008. (popravni) :
Zamolila bih za objasnjenje prvog i 3. zadatka molim vas. Hvala.  |
2008. pod 3.b) rjesih, dobila sam [ -11/4, 1 >, a ne znam kako da pod a)
|
|
| [Vrh] |
|
|








