| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
Boris B.
Forumaš(ica)

Pridružen/a: 19. 01. 2010. (18:01:54)
Postovi: (32)16
Spol: 
|
 Postano: 14:43 ned, 27. 3. 2011 Naslov: Postano: 14:43 ned, 27. 3. 2011 Naslov: |
    |
|
|
@maty321: Mislim da ti je napisao pbakic na prosloj stranici :)
@pajopatak: Za Aut(Z+Z) je isto netko vec stavljao link na odgovor ;)
A za 5a), ako mislis na ono s normalnom podgrupom i jezgrom, onda smo jedan smijer dokazali (jezgra homomorfizma je normalna podgrupa), a za drugi mozes reci da posto je N normalna postoji G/N, a onda imas kanonsku projekciju s G na G/N kojoj je upravo N jezgra. Ovo je ukratko, reci ako sto treba raspisati :)
@maty321: Mislim da ti je napisao pbakic na prosloj stranici 
@pajopatak: Za Aut(Z+Z) je isto netko vec stavljao link na odgovor 
A za 5a), ako mislis na ono s normalnom podgrupom i jezgrom, onda smo jedan smijer dokazali (jezgra homomorfizma je normalna podgrupa), a za drugi mozes reci da posto je N normalna postoji G/N, a onda imas kanonsku projekciju s G na G/N kojoj je upravo N jezgra. Ovo je ukratko, reci ako sto treba raspisati 
_________________
The lyf so short, the craft so long to lerne
|
|
| [Vrh] |
|
Bug
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: 
Lokacija: Kako kad!!
|
 Postano: 15:12 ned, 27. 3. 2011 Naslov: Postano: 15:12 ned, 27. 3. 2011 Naslov: |
    |
|
|
gdje grijesim??
meni ispada da je grupoid, a u rjesenjim pise da je grupa...
[latex]G=Q^*[/latex]×[latex]Q[/latex]×[latex]Q[/latex]
[latex](a_1,a_2,a_3)o(b_1,b_2,b_3)=(a_1b_1,a_2b_1+b_2,a_3b_1+b_3)[/latex]
[latex][(a_1,a_2,a_3)o(b_1,b_2,b_3)]o(c_1,c_2,c_3)=(c_1(a_1b_1),c_2(a_2b_1+b_2),c_3(a_3b_1+b_3))[/latex]
[latex](a_1,a_2,a_3)o[(b_1,b_2,b_3)o(c_1,c_2,c_3)]=(a_1(b_1c_1), a_2b_1c_1+b_2c_1+c_2,a_3b_1c_1+b_3c_1+c_3)[/latex]
gdje grijesim??
meni ispada da je grupoid, a u rjesenjim pise da je grupa...
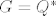 × ×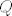 × ×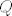
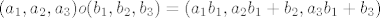
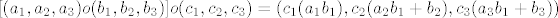
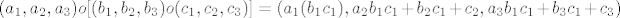
_________________
Everybody Dies...
Nobody is perfect...
Non scholae, sed vitae discimus
|
|
| [Vrh] |
|
sunce
Forumaš(ica)

Pridružen/a: 20. 03. 2010. (18:49:03)
Postovi: (3F)16
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
sunce
Forumaš(ica)

Pridružen/a: 20. 03. 2010. (18:49:03)
Postovi: (3F)16
|
 Postano: 16:59 ned, 27. 3. 2011 Naslov: Re: vježbe za kolokvij Postano: 16:59 ned, 27. 3. 2011 Naslov: Re: vježbe za kolokvij |
    |
|
|
..
[size=9][color=#999999]Added after 9 minutes:[/color][/size]
[quote="Boris B."][quote="michelangelo"]kako se rješavaju zadaci tipa odredi [latex]\mathrm{Int}(\mathbb{Z}_{9})[/latex] ili [latex]\mathrm{Aut}(\mathbb{Z}_{9})[/latex] ???? tnx unaprijed[/quote]
Kako je Z9 komutativna, Int(Z9) je trivijalna (a + x - a = x, za svako x i za svako a).
Aut(Z9) određuješ po tome što automorfizmi kao i svi monomorfizmi čuvaju red elementa, pa posebno i generatore prevode u generatore, a za cikličku grupu je homomorfizam potpuno određen djelovanjem na generatoru.
Dakle odabereš proizvoljan generator Z9 (npr. 1) i popišeš sve moguće načine da ga pošalješ u neki generator Z9. Kako su oni {1, 2, 4, 5, 7, 8} (brojevi manji od 9, a s 9 relativno prosti), Aut(Z9) se sastoji od fi(9) = 6 funkcija, nazovimo ih f1, f2, f4, f5, f7, f8.
Nadalje, lako se provjeri da je za cikličku grupu grupa automorfizama komutativna, pa možeš primijeniti teorem o strukturi konačnih Abelovih grupa, koji u ovom slučaju daje [latex]\mathbb Z/2 \mathbb Z \oplus \mathbb Z/3 \mathbb Z \cong \mathbb Z/6 \mathbb Z[/latex] kao jedinu komutativnu grupu reda 6, pa znamo da je riječ o njoj. Inače, ako postoji više komutativnih grupa koje dolaze u obzir, onda ispitaš redove elemenata u grupi automorfizama kako bi saznao o čemu se radi.
Npr. za Aut(Z5) bi imao fi(5) = 4 automorfizma, a postoje dvije komutativne grupe reda 4: Z/2Z + Z/2Z i Z/4Z. No u prvoj grupi su svi elementi osim jediničnoga reda 2, a u drugoj su [1] i [3] reda 4, pa to možemo usporediti s redovima elemenata u grupi automorfizama.
Neka su oni s f1, f2, f3 i f4 (dani s fi(1) = i). Kako je npr. f(f(2)) = 4, vidimo da je red od f2 > 2, pa grupa automorfizama mora biti Z/4Z.[/quote]
zar nije kod Aut(Z9) komutativna grupa reda 6 jos i Z/6Z ? zasto je samo ova gore navedena? :oops:
..
Added after 9 minutes:
| Boris B. (napisa): | | michelangelo (napisa): | kako se rješavaju zadaci tipa odredi 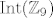 ili ili 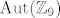 ???? tnx unaprijed ???? tnx unaprijed |
Kako je Z9 komutativna, Int(Z9) je trivijalna (a + x - a = x, za svako x i za svako a).
Aut(Z9) određuješ po tome što automorfizmi kao i svi monomorfizmi čuvaju red elementa, pa posebno i generatore prevode u generatore, a za cikličku grupu je homomorfizam potpuno određen djelovanjem na generatoru.
Dakle odabereš proizvoljan generator Z9 (npr. 1) i popišeš sve moguće načine da ga pošalješ u neki generator Z9. Kako su oni {1, 2, 4, 5, 7, 8} (brojevi manji od 9, a s 9 relativno prosti), Aut(Z9) se sastoji od fi(9) = 6 funkcija, nazovimo ih f1, f2, f4, f5, f7, f8.
Nadalje, lako se provjeri da je za cikličku grupu grupa automorfizama komutativna, pa možeš primijeniti teorem o strukturi konačnih Abelovih grupa, koji u ovom slučaju daje 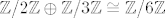 kao jedinu komutativnu grupu reda 6, pa znamo da je riječ o njoj. Inače, ako postoji više komutativnih grupa koje dolaze u obzir, onda ispitaš redove elemenata u grupi automorfizama kako bi saznao o čemu se radi. kao jedinu komutativnu grupu reda 6, pa znamo da je riječ o njoj. Inače, ako postoji više komutativnih grupa koje dolaze u obzir, onda ispitaš redove elemenata u grupi automorfizama kako bi saznao o čemu se radi.
Npr. za Aut(Z5) bi imao fi(5) = 4 automorfizma, a postoje dvije komutativne grupe reda 4: Z/2Z + Z/2Z i Z/4Z. No u prvoj grupi su svi elementi osim jediničnoga reda 2, a u drugoj su [1] i [3] reda 4, pa to možemo usporediti s redovima elemenata u grupi automorfizama.
Neka su oni s f1, f2, f3 i f4 (dani s fi(1) = i). Kako je npr. f(f(2)) = 4, vidimo da je red od f2 > 2, pa grupa automorfizama mora biti Z/4Z. |
zar nije kod Aut(Z9) komutativna grupa reda 6 jos i Z/6Z ? zasto je samo ova gore navedena? 
|
|
| [Vrh] |
|
Boris B.
Forumaš(ica)

Pridružen/a: 19. 01. 2010. (18:01:54)
Postovi: (32)16
Spol: 
|
 Postano: 17:26 ned, 27. 3. 2011 Naslov: Postano: 17:26 ned, 27. 3. 2011 Naslov: |
    |
|
|
Pogledaj onu latexiranu stvar u sredini posta, tamo se spominje Z/Z6 :) no ona je izomorfna Z/Z2 + Z/Z3: pogledaj recimo ([1], [1]) iz Z/Z2 + Z/Z3. Za njega je ([1], [1])^n = ([1]^n, [1]^n) = ([n], [n]), pa je ([1], [1])^n = ([0], [0]) akko 2 dijeli n i 3 dijeli n, a najmanji prirodan n za koji to vrijedi ja naravno 6. Dakle, red elementa ([1], [1]) je 6, a pošto se to podudara s redom grupe Z/Z2 + Z/Z3, onda je ona ciklička, dakle izomorfna sa Z/Z6.
Općenito je za M(m, n) = 1 [latex]\mathbb Z/m \mathbb Z \oplus \mathbb Z/n \mathbb Z \cong \mathbb Z/mn \mathbb Z[/latex].
Pogledaj onu latexiranu stvar u sredini posta, tamo se spominje Z/Z6  no ona je izomorfna Z/Z2 + Z/Z3: pogledaj recimo ([1], [1]) iz Z/Z2 + Z/Z3. Za njega je ([1], [1])^n = ([1]^n, [1]^n) = ([n], [n]), pa je ([1], [1])^n = ([0], [0]) akko 2 dijeli n i 3 dijeli n, a najmanji prirodan n za koji to vrijedi ja naravno 6. Dakle, red elementa ([1], [1]) je 6, a pošto se to podudara s redom grupe Z/Z2 + Z/Z3, onda je ona ciklička, dakle izomorfna sa Z/Z6. no ona je izomorfna Z/Z2 + Z/Z3: pogledaj recimo ([1], [1]) iz Z/Z2 + Z/Z3. Za njega je ([1], [1])^n = ([1]^n, [1]^n) = ([n], [n]), pa je ([1], [1])^n = ([0], [0]) akko 2 dijeli n i 3 dijeli n, a najmanji prirodan n za koji to vrijedi ja naravno 6. Dakle, red elementa ([1], [1]) je 6, a pošto se to podudara s redom grupe Z/Z2 + Z/Z3, onda je ona ciklička, dakle izomorfna sa Z/Z6.
Općenito je za M(m, n) = 1 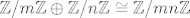 . .
_________________
The lyf so short, the craft so long to lerne
|
|
| [Vrh] |
|
marty
Forumaš(ica)
Pridružen/a: 26. 10. 2009. (17:40:41)
Postovi: (3D)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 18:12 ned, 27. 3. 2011 Naslov: Postano: 18:12 ned, 27. 3. 2011 Naslov: |
    |
|
|
Imam par nejasnoća, jesu li sve Zn cikličke i komutativne? I svi kartezijevi produkti istih komutativni? Pp da jesu,ali da budem sigurna ;)
@marty:ja mislim da je i ZxZ3 ciklička :?:
jer su 1 i 3 relativno prosti(?)
ali ni meni nije sve to jasno,užasno je apstraktno :?
U grupi G= Z3xZ6 definiran je skup H={(a, b)e Z3xZ6::b=0 ili b=3}. ispisite klase u G/H i odredite cemu je izomorfna kvocijentna grupa G/H?
i ako može netko ovaj zadatak riješiti,ako ja ne radim dobro,ja sam počela ispisivati za svaki element iz G, i svaki element iz H njihov zbroj,i dobijem puno različitih stvari, i ne razumijem što su mi klase.
Npr. (0,1)+(1,0)=(1,1) - prvi pribrojnik je iz G,drugi iz H
(1,1)+(0,0)=(1,1)
znači li to da (0,1) i (1,1) spadaju u istu klasu?
Trebam li zaista [b]sve[/b] moguće kombinacije pozbrajati?
edit:mislim da nisam dobro,jer je xH jedna klasa, a po mom ovako ispada da su x+h1(npr.0,0) i x+h2(npr.1,3) razičite klase..
ne kužim :roll:
Imam par nejasnoća, jesu li sve Zn cikličke i komutativne? I svi kartezijevi produkti istih komutativni? Pp da jesu,ali da budem sigurna 
@marty:ja mislim da je i ZxZ3 ciklička 
jer su 1 i 3 relativno prosti(?)
ali ni meni nije sve to jasno,užasno je apstraktno 
U grupi G= Z3xZ6 definiran je skup H={(a, b)e Z3xZ6::b=0 ili b=3}. ispisite klase u G/H i odredite cemu je izomorfna kvocijentna grupa G/H?
i ako može netko ovaj zadatak riješiti,ako ja ne radim dobro,ja sam počela ispisivati za svaki element iz G, i svaki element iz H njihov zbroj,i dobijem puno različitih stvari, i ne razumijem što su mi klase.
Npr. (0,1)+(1,0)=(1,1) - prvi pribrojnik je iz G,drugi iz H
(1,1)+(0,0)=(1,1)
znači li to da (0,1) i (1,1) spadaju u istu klasu?
Trebam li zaista sve moguće kombinacije pozbrajati?
edit:mislim da nisam dobro,jer je xH jedna klasa, a po mom ovako ispada da su x+h1(npr.0,0) i x+h2(npr.1,3) razičite klase..
ne kužim 
|
|
| [Vrh] |
|
sunce
Forumaš(ica)

Pridružen/a: 20. 03. 2010. (18:49:03)
Postovi: (3F)16
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 18:35 ned, 27. 3. 2011 Naslov: Postano: 18:35 ned, 27. 3. 2011 Naslov: |
    |
|
|
osvrt na moj post:
[u]možda[/u], klase gledam ponovo kao kartezijev produkt?
pa mi je klasa od (0,0) H, od (0,1) Z3 x {1,4}(kao podskup od Z6,a u tu klasu spadaju još i (1,1),(2,1)) itd?
konačno,dobila sam da su klase H, Z3 x {1,4}, Z3 x {2,5}, dakle imam ih 3 te je to izomorfno Z3?
sorry na stalnom editiranju,ali mi stalno nekaj novog dođe do mozga :lol:
osvrt na moj post:
možda, klase gledam ponovo kao kartezijev produkt?
pa mi je klasa od (0,0) H, od (0,1) Z3 x {1,4}(kao podskup od Z6,a u tu klasu spadaju još i (1,1),(2,1)) itd?
konačno,dobila sam da su klase H, Z3 x {1,4}, Z3 x {2,5}, dakle imam ih 3 te je to izomorfno Z3?
sorry na stalnom editiranju,ali mi stalno nekaj novog dođe do mozga 
Zadnja promjena: .anchy.; 18:46 ned, 27. 3. 2011; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
sunce
Forumaš(ica)

Pridružen/a: 20. 03. 2010. (18:49:03)
Postovi: (3F)16
|
|
| [Vrh] |
|
Pero Kvrzica
Forumaš(ica)
Pridružen/a: 26. 06. 2010. (12:45:56)
Postovi: (19)16
|
|
| [Vrh] |
|
Crvenkapica
Forumaš(ica)

Pridružen/a: 16. 04. 2007. (14:52:45)
Postovi: (AB)16
|
|
| [Vrh] |
|
|








