| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
addriana
Forumaš(ica)
Pridružen/a: 27. 10. 2008. (15:05:39)
Postovi: (28)16
|
|
| [Vrh] |
|
glava
Forumaš(ica)

Pridružen/a: 28. 03. 2007. (18:48:16)
Postovi: (89)16
Spol: 
|
|
| [Vrh] |
|
__MP__
Forumaš(ica)

Pridružen/a: 11. 02. 2008. (21:46:38)
Postovi: (1F)16
Lokacija: Požega
|
|
| [Vrh] |
|
Taurus
Forumaš(ica)

Pridružen/a: 05. 02. 2008. (23:11:51)
Postovi: (61)16
Spol: 
Lokacija: Psychiatric Mental Facility (PMF)
|
 Postano: 18:06 ned, 30. 5. 2010 Naslov: Re: Zadaci iz 2. kolokvija Postano: 18:06 ned, 30. 5. 2010 Naslov: Re: Zadaci iz 2. kolokvija |
    |
|
|
[quote="addriana"]Molim pomoć oko dva zadatka iz 2. kolokvija 2008.
[latex]e^yu_{xy}-u_{yy}+u_{y}=0[/latex]
[latex]u(x,0)=-\frac{x^2}{2}[/latex]
[latex]u_y(x,0)=-sinx[/latex]
Nema [latex]u_{xx}[/latex], znači a=0. Kako onda odredim [latex]y'=\frac{b^2-ac}{a}[/latex] ?
[latex](x+y)u_x+yu_y=xyu[/latex]
[latex]u|_{y=x}=e^{\frac{x^2}{4}[/latex]
Kako se riješiti y u [latex](x+y)u_x[/latex] ?[/quote]
Ovaj prvi ide preko zamjene x <-> y i tako dobijes :
[latex]e^xu_{xy}-u_{xx}+u_{x}=0[/latex] iz cega vidis da je a = -1, ..
Na kraju se dobije rješenje tipa
[latex](1/2) (ksi-eta)^2u_{ksieta}=0[/latex] (moguće pogrešno)
Eh sada i mene zanima kako odrediti rješenje iz pocetnih uvijeta, da li se i tamo mijenjaju x <-> y ili .. ? Pokušao sam tu nešto raspisivati i računati ali đabe.
Za ovaj drugi zadatak jedino napises vektore V i k, i onda izdjednačiš derivirano k i V i dalje računaš po šabloni (običan tip kvazilinearne jdbe 1. reda).
A sada još jedno pitanje s moje strane, kako se rješava onaj 4. zadatak iz prošlogodišnjeg kolokvija. Znam da je to Poisson i nema onog drugog integrala i sve je to super i 5, ali ona dva e-a šta se množe, ne znam što točno s njima, pokušao sam odmah neku supstituciju ali nema kruha, pa sam pokušao raspisati nešto tipa zadatka koji smo "radili" na vježbama ali je ovaj ipak složeniji pa mi nije išlo ni tako. Uff...
| addriana (napisa): | Molim pomoć oko dva zadatka iz 2. kolokvija 2008.
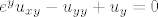
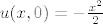
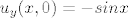
Nema 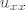 , znači a=0. Kako onda odredim , znači a=0. Kako onda odredim 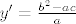 ? ?
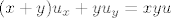
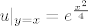
Kako se riješiti y u 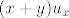 ? ? |
Ovaj prvi ide preko zamjene x ↔ y i tako dobijes :
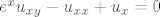 iz cega vidis da je a = -1, .. iz cega vidis da je a = -1, ..
Na kraju se dobije rješenje tipa
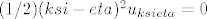 (moguće pogrešno) (moguće pogrešno)
Eh sada i mene zanima kako odrediti rješenje iz pocetnih uvijeta, da li se i tamo mijenjaju x ↔ y ili .. ? Pokušao sam tu nešto raspisivati i računati ali đabe.
Za ovaj drugi zadatak jedino napises vektore V i k, i onda izdjednačiš derivirano k i V i dalje računaš po šabloni (običan tip kvazilinearne jdbe 1. reda).
A sada još jedno pitanje s moje strane, kako se rješava onaj 4. zadatak iz prošlogodišnjeg kolokvija. Znam da je to Poisson i nema onog drugog integrala i sve je to super i 5, ali ona dva e-a šta se množe, ne znam što točno s njima, pokušao sam odmah neku supstituciju ali nema kruha, pa sam pokušao raspisati nešto tipa zadatka koji smo "radili" na vježbama ali je ovaj ipak složeniji pa mi nije išlo ni tako. Uff...
_________________
Moooooooooooooooooooooooo...
|
|
| [Vrh] |
|
Ančica
Forumaš(ica)


Pridružen/a: 01. 12. 2006. (16:12:53)
Postovi: (F6)16
Spol: 
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
Ančica
Forumaš(ica)


Pridružen/a: 01. 12. 2006. (16:12:53)
Postovi: (F6)16
Spol: 
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
Ančica
Forumaš(ica)


Pridružen/a: 01. 12. 2006. (16:12:53)
Postovi: (F6)16
Spol: 
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
nike
Forumaš(ica)

Pridružen/a: 11. 02. 2010. (13:05:01)
Postovi: (58)16
|
|
| [Vrh] |
|
lorozic
Forumaš(ica)

Pridružen/a: 08. 12. 2008. (17:11:14)
Postovi: (50)16
Spol: 
|
|
| [Vrh] |
|
irena0102
Forumaš(ica)


Pridružen/a: 01. 02. 2010. (11:49:52)
Postovi: (45)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
 Postano: 15:42 pon, 30. 5. 2011 Naslov: Postano: 15:42 pon, 30. 5. 2011 Naslov: |
    |
|
|
3. zadatak prošle godine rješavaš separacijom varijabli [latex]u(x, t) = X(x) \cdot T(t)[/latex]. Rješenje je sljedeće:
[latex] u(x, t)=\sum_{n=1}^{\infty} B_n \exp\left(-\left(\frac{n\pi}{l}\right)^2 t \right) \sin\frac{n\pi x}{l} [/latex], gdje nepoznate koeficijente B_n tražiš iz početnog uvjeta, tj. [latex]u(x, 0)=cos\frac{2\pi x}{l}[/latex].
Kako riješiti 4. zadatak iz istog kolokvija? Ide li to preko fundamentalnog rješenja? Problem je u tome što ne znam izračunati integral koji se pojavi, piše li možda u nekakvim tablicama (nemam niti jedne pri ruci)? Smijemo li tablice imati na ispitu?
3. zadatak prošle godine rješavaš separacijom varijabli 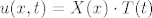 . Rješenje je sljedeće: . Rješenje je sljedeće:
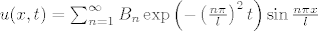 , gdje nepoznate koeficijente B_n tražiš iz početnog uvjeta, tj. , gdje nepoznate koeficijente B_n tražiš iz početnog uvjeta, tj. 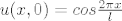 . .
Kako riješiti 4. zadatak iz istog kolokvija? Ide li to preko fundamentalnog rješenja? Problem je u tome što ne znam izračunati integral koji se pojavi, piše li možda u nekakvim tablicama (nemam niti jedne pri ruci)? Smijemo li tablice imati na ispitu?
|
|
| [Vrh] |
|
irena0102
Forumaš(ica)


Pridružen/a: 01. 02. 2010. (11:49:52)
Postovi: (45)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
irena0102
Forumaš(ica)


Pridružen/a: 01. 02. 2010. (11:49:52)
Postovi: (45)16
Spol: 
|
|
| [Vrh] |
|
tinky
Forumaš(ica)
Pridružen/a: 20. 06. 2008. (11:59:08)
Postovi: (3F)16
|
|
| [Vrh] |
|
lucika
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (17:52:27)
Postovi: (12F)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|
















