| Prethodna tema :: Sljedeća tema |
| Koliko vas je puta prof. Veljan vracao sa usmenog? |
| Niti jednom. |
|
26% |
[ 4 ] |
| Samo jedan put. |
|
6% |
[ 1 ] |
| Dva ili više puta. |
|
20% |
[ 3 ] |
| Nisam jos izlazio na ispit. |
|
46% |
[ 7 ] |
|
| Ukupno glasova : 15 |
|
| Autor/ica |
Poruka |
grossi
Forumaš(ica)

Pridružen/a: 22. 04. 2004. (16:33:41)
Postovi: (5D)16
Spol: 
Lokacija: Delta Neretva
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 13:30 sub, 19. 6. 2004 Naslov: Postano: 13:30 sub, 19. 6. 2004 Naslov: |
    |
|
|
Potrazi u skriptarnici vrlo dobre rijesene pismene usmene Veljanove :) Ima jedan set pitanja koji se ponavlja cesto al ne i uvijek i ta pitanja sa odgovorima su tamo
Potrazi u skriptarnici vrlo dobre rijesene pismene usmene Veljanove  Ima jedan set pitanja koji se ponavlja cesto al ne i uvijek i ta pitanja sa odgovorima su tamo Ima jedan set pitanja koji se ponavlja cesto al ne i uvijek i ta pitanja sa odgovorima su tamo
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
grossi
Forumaš(ica)

Pridružen/a: 22. 04. 2004. (16:33:41)
Postovi: (5D)16
Spol: 
Lokacija: Delta Neretva
|
|
| [Vrh] |
|
grossi
Forumaš(ica)

Pridružen/a: 22. 04. 2004. (16:33:41)
Postovi: (5D)16
Spol: 
Lokacija: Delta Neretva
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 13:14 pon, 28. 6. 2004 Naslov: Postano: 13:14 pon, 28. 6. 2004 Naslov: |
    |
|
|
Nazalost nemam nacin to prebaciti u digitalni format, ali [b]sigurno[/b] u skriptarnici imas pitanja sa odgovorima koja su cesto ponavljana na usmenim ispitima kod nasega Darka :)
..samo se moras potruditi i to naci u onih 4-5 fascikli :? (nemeres fulat, nema puno takvih pitanja/odgovora medju papirima)
Nazalost nemam nacin to prebaciti u digitalni format, ali sigurno u skriptarnici imas pitanja sa odgovorima koja su cesto ponavljana na usmenim ispitima kod nasega Darka 
..samo se moras potruditi i to naci u onih 4-5 fascikli  (nemeres fulat, nema puno takvih pitanja/odgovora medju papirima) (nemeres fulat, nema puno takvih pitanja/odgovora medju papirima)
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
Crni
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 21:25 pon, 28. 6. 2004 Naslov: Postano: 21:25 pon, 28. 6. 2004 Naslov: |
    |
|
|
[quote="Crni"]Klikni [url=http://degiorgi.math.hr/forum/viewtopic.php?t=1450]ovdje[/url].[/quote]
...to su pitanja sa usmenih prof. Nogo. Veljan ima potpuno drugaciju metodu drzanja usmenih ispita i ima skup od 40-ak pitanja iz svoje knjige koji se pojavljuje kroz godine u 70% njegovih "pismenih usmenih", dok prof. Nogo, ako sam dobro shvatio, nema tu praksu.
| Crni (napisa): | | Klikni ovdje. |
...to su pitanja sa usmenih prof. Nogo. Veljan ima potpuno drugaciju metodu drzanja usmenih ispita i ima skup od 40-ak pitanja iz svoje knjige koji se pojavljuje kroz godine u 70% njegovih "pismenih usmenih", dok prof. Nogo, ako sam dobro shvatio, nema tu praksu.
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
grossi
Forumaš(ica)

Pridružen/a: 22. 04. 2004. (16:33:41)
Postovi: (5D)16
Spol: 
Lokacija: Delta Neretva
|
|
| [Vrh] |
|
bily
Forumaš(ica)


Pridružen/a: 29. 04. 2003. (16:21:46)
Postovi: (4B7)16
Spol: 
|
|
| [Vrh] |
|
grossi
Forumaš(ica)

Pridružen/a: 22. 04. 2004. (16:33:41)
Postovi: (5D)16
Spol: 
Lokacija: Delta Neretva
|
|
| [Vrh] |
|
bily
Forumaš(ica)


Pridružen/a: 29. 04. 2003. (16:21:46)
Postovi: (4B7)16
Spol: 
|
|
| [Vrh] |
|
grossi
Forumaš(ica)

Pridružen/a: 22. 04. 2004. (16:33:41)
Postovi: (5D)16
Spol: 
Lokacija: Delta Neretva
|
|
| [Vrh] |
|
grossi
Forumaš(ica)

Pridružen/a: 22. 04. 2004. (16:33:41)
Postovi: (5D)16
Spol: 
Lokacija: Delta Neretva
|
 Postano: 8:51 čet, 8. 7. 2004 Naslov: Postano: 8:51 čet, 8. 7. 2004 Naslov: |
    |
|
|
[b]Pitanja sa usmenog 7.7.2004[/b]
1. Broj podskopova iz [n] bez susjednih brojeva.
2. Neki proracun (teski), primjenjuje se Vandermondova funkcija.
3. Na koliko nacina n svera dijeli prostor.
4. EFI za broj Deranzmana, te iz toga asimptotiku odrediti.
5. FI za Catalanove brojeve, barem dva primjera di se pojavljuju i asimptotika.
Bilo bi dobro da sa svakog roka netko napise nova pitanja na forum.
[b]Savjet za kolege:[/b] Profesor je dobar, lagana su pitanja, ponavljaju se i ne treba puno znati za poloziti, mislim da su dovoljna dva potpuna odgovora.
Pitanja sa usmenog 7.7.2004
1. Broj podskopova iz [n] bez susjednih brojeva.
2. Neki proracun (teski), primjenjuje se Vandermondova funkcija.
3. Na koliko nacina n svera dijeli prostor.
4. EFI za broj Deranzmana, te iz toga asimptotiku odrediti.
5. FI za Catalanove brojeve, barem dva primjera di se pojavljuju i asimptotika.
Bilo bi dobro da sa svakog roka netko napise nova pitanja na forum.
Savjet za kolege: Profesor je dobar, lagana su pitanja, ponavljaju se i ne treba puno znati za poloziti, mislim da su dovoljna dva potpuna odgovora.
|
|
| [Vrh] |
|
bily
Forumaš(ica)


Pridružen/a: 29. 04. 2003. (16:21:46)
Postovi: (4B7)16
Spol: 
|
 Postano: 8:55 čet, 8. 7. 2004 Naslov: Postano: 8:55 čet, 8. 7. 2004 Naslov: |
    |
|
|
[quote="grossi"][b]Pitanja sa usmenog 7.7.2004[/b]
1. Broj podskopova iz [n] bez susjednih brojeva.
2. Neki proracun (teski), primjenjuje se Vandermondova funkcija.
3. Na koliko nacina n svera dijeli prostor.
4. EFI za broj Deranzmana, te iz toga asimptotiku odrediti.
5. FI za Catalanove brojeve, barem dva primjera di se pojavljuju i asimptotika.
Bilo bi dobro da sa svakog roka netko napise nova pitanja na forum.
[b]Savjet za kolege:[/b] Profesor je dobar, lagana su pitanja, ponavljaju se i ne treba puno znati za poloziti, mislim da su dovoljna dva potpuna odgovora.[/quote]
[b]cestitam ti na polozenom ispitu nadam se da su ti ona pitanja koja sam ti dala makar malo pomogla..... :2pivce: [/b]
| grossi (napisa): | Pitanja sa usmenog 7.7.2004
1. Broj podskopova iz [n] bez susjednih brojeva.
2. Neki proracun (teski), primjenjuje se Vandermondova funkcija.
3. Na koliko nacina n svera dijeli prostor.
4. EFI za broj Deranzmana, te iz toga asimptotiku odrediti.
5. FI za Catalanove brojeve, barem dva primjera di se pojavljuju i asimptotika.
Bilo bi dobro da sa svakog roka netko napise nova pitanja na forum.
Savjet za kolege: Profesor je dobar, lagana su pitanja, ponavljaju se i ne treba puno znati za poloziti, mislim da su dovoljna dva potpuna odgovora. |
cestitam ti na polozenom ispitu nadam se da su ti ona pitanja koja sam ti dala makar malo pomogla..... 
_________________ NAJNERAZUMLJIVIJE JE NA OVOM SVIJETU STO JE ON RAZUMLJIV!!!!
Albert Einstein
   |
|
| [Vrh] |
|
ninocka
Forumaš(ica)

Pridružen/a: 15. 04. 2004. (16:03:44)
Postovi: (3D)16
Lokacija: ne drzi me mjesto
|
 Postano: 8:23 pet, 9. 7. 2004 Naslov: Pitanja usmeni prof.Veljan 07.07. Postano: 8:23 pet, 9. 7. 2004 Naslov: Pitanja usmeni prof.Veljan 07.07. |
    |
|
|
Evo za sve one koji traze zakonitosti u ponavljanju pitanja na usmenom: :grebgreb:
1.Koliko ima podskupova iz [n] koji ne sadrze dva susjedna broja?
Naznaciti koliko je to za n=100
2. Dokazati (ne znam kako ovo korektno zapisati): :crazyeyes:
X na n nadcrtano = suma po k>=0 L(n,k)X na k podcrtano
gdje je L(n,k)=n!/k! (n-1 povrh k-1)
uputa je: Vandermonde
3. Na koliko najvise dijelova n sfera dijeli prostor?
4. Odrediti EFI za deranžmane, pomocu toga odrediti Dn i asimptotsko
ponasanje od Dn
5. FI za Catalanove brojeve. navesti bar 2 kombinatorna znacenja Catalanovih brojeva, odrediti Cn (iz FI) i asimptotika
sretno svima, pozdravcic :navijacica:
:cmok:
Evo za sve one koji traze zakonitosti u ponavljanju pitanja na usmenom: 
1.Koliko ima podskupova iz [n] koji ne sadrze dva susjedna broja?
Naznaciti koliko je to za n=100
2. Dokazati (ne znam kako ovo korektno zapisati): 
X na n nadcrtano = suma po k>=0 L(n,k)X na k podcrtano
gdje je L(n,k)=n!/k! (n-1 povrh k-1)
uputa je: Vandermonde
3. Na koliko najvise dijelova n sfera dijeli prostor?
4. Odrediti EFI za deranžmane, pomocu toga odrediti Dn i asimptotsko
ponasanje od Dn
5. FI za Catalanove brojeve. navesti bar 2 kombinatorna znacenja Catalanovih brojeva, odrediti Cn (iz FI) i asimptotika
sretno svima, pozdravcic 

|
|
| [Vrh] |
|
kikach
Forumaš(ica)

Pridružen/a: 13. 02. 2004. (19:05:17)
Postovi: (4B)16
Spol: 
|
 Postano: 13:56 uto, 13. 7. 2004 Naslov: Postano: 13:56 uto, 13. 7. 2004 Naslov: |
    |
|
|
[u]Pitanja s usmenog 12.07.2004. [/u] 8)
1. Kolika je veličina najvećeg antilanca podskupova n-članog skupa? Je li manji od (2^n)/sqrt(n) ?
2. Koliko ima binarnih nizova (a1,...,a7) t.d. je a1<=a2>=a3<=a4>=a5<=a6>=a7 ?
(To je jedan primjer, točnije, primjer 9. strana 119 u profesorovoj knjizi, u izdanju Algoritma, 2001.god)
3. Koliko ima surjekcija [n]-> [k]? Što je u slučaju n=k? Kolika je vjerojatnost da je nasumce odabrana funkcija [n]->[k] surjekcija? Je li ona veća od 1/2 za n=5, k=3?
4. FI za Catalanove brojeve i pomoću nje odrediti Cn. Naći barem 2 kombinatorna značenja tih brojeva. Asimptotika za Cn.
5. EFI za deranžmane, pomoću toga Dn i njegovu asimptotiku. Koliko je Dn(k)=broj permutacija od [n] s točno k fiksnih točaka ?
Eto....usmeni nije strašan. Ima se dovoljno vremena sve napisati, naravno, ako ste sve naučili.
Sretno :)
Pitanja s usmenog 12.07.2004. 
1. Kolika je veličina najvećeg antilanca podskupova n-članog skupa? Je li manji od (2^n)/sqrt(n) ?
2. Koliko ima binarnih nizova (a1,...,a7) t.d. je a1⇐a2>=a3⇐a4>=a5⇐a6>=a7 ?
(To je jedan primjer, točnije, primjer 9. strana 119 u profesorovoj knjizi, u izdanju Algoritma, 2001.god)
3. Koliko ima surjekcija [n]→ [k]? Što je u slučaju n=k? Kolika je vjerojatnost da je nasumce odabrana funkcija [n]→[k] surjekcija? Je li ona veća od 1/2 za n=5, k=3?
4. FI za Catalanove brojeve i pomoću nje odrediti Cn. Naći barem 2 kombinatorna značenja tih brojeva. Asimptotika za Cn.
5. EFI za deranžmane, pomoću toga Dn i njegovu asimptotiku. Koliko je Dn(k)=broj permutacija od [n] s točno k fiksnih točaka ?
Eto....usmeni nije strašan. Ima se dovoljno vremena sve napisati, naravno, ako ste sve naučili.
Sretno 
|
|
| [Vrh] |
|
hexy
Forumaš(ica)

Pridružen/a: 19. 11. 2002. (09:39:35)
Postovi: (8A)16
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 12:46 sri, 15. 9. 2004 Naslov: Postano: 12:46 sri, 15. 9. 2004 Naslov: |
    |
|
|
Evo pitanja sa usmenog od 15.9.2004. (ne garantiram za poredak)
(1) na koliko djelova n sfera dijeli prostor :shocked!: opet :shock:
(2) kombinatorno dokazi:
[latex]\newcommand{\binom}[2]{ \left( \begin{array}{c} #1 \\ #2 \end{array} \right ) }
\displaystyle \sum^{k}_{t=0} \binom{k}{t} \sum_{j=0}^t (-1)^j \binom{t}{j} (t-j)^n = k^n[/latex]
(hint: FUI)
(3) koliko ima najkracih puteva po cjelobrojnoj mrezi od (0,0) do (n,n) takvih da ne prelaze dijagonalu y=x
(4) Suma, suma kvadrata i cassinijev identitet kod Fibbonaccijevih brojeva i
(5) (za ovo nisam siguran) Izracunaj FI od
[latex]\newcommand{\binom}[2]{ \left( \begin{array}{c} #1 \\ #2 \end{array} \right ) }
\displaystyle a_n = \sum_{k=0}^n \binom{n-k}{k}[/latex]
[color=red]disklejmer, za ovo [u]zbilja[/u] nisam siguran, bilo bi lijepo da me netko ispravi[/color] :?
Dakle.. zadatak broj (1) (u tekstu, ne u ispitu) je (dosta) detaljno rijesen na topicu "[url=http://degiorgi.math.hr/forum/viewtopic.php?t=2051]Kruznice i sfere[/url]".
btw: koliko je [latex]\sum_{k=1}^n k^2 =~ ?~[/latex] :? ?
(2) ide preko FUI-a. Tj. izvedete FUI za broj surjekcija sa n-clanog u t-clani skup, odaberete t-clani podskup od [k] i sumirate :)
(3) Jedan od primjera u knjizi D. Veljana u poglavlju o kombinacijama, ako se ne varam, rjesenje je, mislim, (n-1)-vi Catalanov broj, postupak u knjizi:
[latex]\newcommand{\binom}[2]{ \left( \begin{array}{c} #1 \\ #2 \end{array} \right ) }
\displaystyle C_{n-1}=\frac{1}{n} \binom{2n-2}{n-1}[/latex]
(4) Isto, poglavlje o rekurzijama, zasebna propozicija
(5) ne znam ni dal sam ga dobro upamtio :?
Evo pitanja sa usmenog od 15.9.2004. (ne garantiram za poredak)
(1) na koliko djelova n sfera dijeli prostor  opet opet 
(2) kombinatorno dokazi:
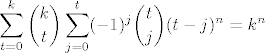
(hint: FUI)
(3) koliko ima najkracih puteva po cjelobrojnoj mrezi od (0,0) do (n,n) takvih da ne prelaze dijagonalu y=x
(4) Suma, suma kvadrata i cassinijev identitet kod Fibbonaccijevih brojeva i
(5) (za ovo nisam siguran) Izracunaj FI od
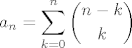
disklejmer, za ovo zbilja nisam siguran, bilo bi lijepo da me netko ispravi 
Dakle.. zadatak broj (1) (u tekstu, ne u ispitu) je (dosta) detaljno rijesen na topicu "Kruznice i sfere".
btw: koliko je 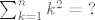  ? ?
(2) ide preko FUI-a. Tj. izvedete FUI za broj surjekcija sa n-clanog u t-clani skup, odaberete t-clani podskup od [k] i sumirate 
(3) Jedan od primjera u knjizi D. Veljana u poglavlju o kombinacijama, ako se ne varam, rjesenje je, mislim, (n-1)-vi Catalanov broj, postupak u knjizi:
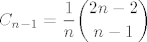
(4) Isto, poglavlje o rekurzijama, zasebna propozicija
(5) ne znam ni dal sam ga dobro upamtio 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
|
| [Vrh] |
|
Caki
Forumaš(ica)

Pridružen/a: 13. 02. 2004. (00:37:53)
Postovi: (14)16
|
|
| [Vrh] |
|
|
















