| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
gflegar
Forumaš(ica)


Pridružen/a: 12. 10. 2011. (15:03:41)
Postovi: (10D)16
Spol: 
|
 Postano: 18:30 sub, 5. 11. 2011 Naslov: Postano: 18:30 sub, 5. 11. 2011 Naslov: |
    |
|
|
[quote="ceps"]Znači, [latex]M = \{x = (x_1, ... , x_{2n}) \in \mathbb{R}^{2n}| x_i +2x_{i+n} = 0, i = 1, ... , n\}[/latex]
Nemoj da te ovo zbuni sa 2n, to znači da gledamo prostore parne dimenzije.
Pa ajmo uzet nekoliko manjih takvih npr.
za [latex]\mathbb{R}^4[/latex]
To bi bili svi oni [latex](x_1, x_2, x_3, x_4)[/latex] za koje vrijedi:
[latex]x_1 + 2x_3 = 0[/latex]
[latex]x_2 + 2x_4 = 0[/latex]
to, jest
[latex]x_1 = -2x_3[/latex]
[latex]x_2 = -2x_4[/latex]
Znači, bili bi oblika
[latex](-2x_3, -2x_4, x_2, x_4)[/latex] - jedna baza za takve članove R-4 bi bila
[latex](-2, 0, 1, 0) , (0, -2, 0, 1)[/latex] i M bi bio 2dimenzionalan.
Ako ti nije jasno kako bi sad to generalizirao na R-2n, probaj si još napraviti za R-6, recimo, pa možda vidiš uzorak! :)[/quote]
Hahaha, a ja vec mislio da se to nekome dalo raspisivati u TeX-u u opcenitom slucaju :D
| ceps (napisa): | Znači, 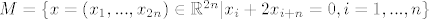
Nemoj da te ovo zbuni sa 2n, to znači da gledamo prostore parne dimenzije.
Pa ajmo uzet nekoliko manjih takvih npr.
za 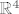
To bi bili svi oni 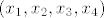 za koje vrijedi: za koje vrijedi:
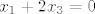
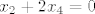
to, jest
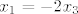
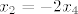
Znači, bili bi oblika
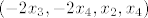 - jedna baza za takve članove R-4 bi bila - jedna baza za takve članove R-4 bi bila
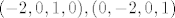 i M bi bio 2dimenzionalan. i M bi bio 2dimenzionalan.
Ako ti nije jasno kako bi sad to generalizirao na R-2n, probaj si još napraviti za R-6, recimo, pa možda vidiš uzorak!  |
Hahaha, a ja vec mislio da se to nekome dalo raspisivati u TeX-u u opcenitom slucaju 
|
|
| [Vrh] |
|
pandora
Forumaš(ica)

Pridružen/a: 22. 10. 2011. (16:55:23)
Postovi: (1A)16
|
 Postano: 20:06 sub, 5. 11. 2011 Naslov: Postano: 20:06 sub, 5. 11. 2011 Naslov: |
    |
|
|
Primjetimo da se baza za [tex] L [/tex] moze pirkazati pomocu baze za [tex] M [/tex].
[tex] (1,2,1,2) = 2(1,1,1,1) - (1,0,1,0) [/tex]
[tex] (1,3,1,3) = 3(1,1,1,1) - 2(1,0,1,0) [/tex]
a kako je [tex] dim L = dim M [/tex] zakljucujemo da je [tex] M = L = M \cap L [/tex].
meni nije jasan ovaj korak
zašto zaključujemo M=L ?
Primjetimo da se baza za [tex] L [/tex] moze pirkazati pomocu baze za [tex] M [/tex].
[tex] (1,2,1,2) = 2(1,1,1,1) - (1,0,1,0) [/tex]
[tex] (1,3,1,3) = 3(1,1,1,1) - 2(1,0,1,0) [/tex]
a kako je [tex] dim L = dim M [/tex] zakljucujemo da je [tex] M = L = M \cap L [/tex].
meni nije jasan ovaj korak
zašto zaključujemo M=L ?
|
|
| [Vrh] |
|
Deni001
Forumaš(ica)
Pridružen/a: 06. 09. 2011. (23:16:57)
Postovi: (23)16
Spol: 
|
|
| [Vrh] |
|
PermutiranoPrase
Forumaš(ica)


Pridružen/a: 10. 09. 2011. (16:08:19)
Postovi: (F4)16
Spol: 
|
|
| [Vrh] |
|
logikaus
Forumaš(ica)

Pridružen/a: 12. 10. 2011. (17:55:23)
Postovi: (45)16
|
|
| [Vrh] |
|
PermutiranoPrase
Forumaš(ica)


Pridružen/a: 10. 09. 2011. (16:08:19)
Postovi: (F4)16
Spol: 
|
 Postano: 9:49 ned, 6. 11. 2011 Naslov: Postano: 9:49 ned, 6. 11. 2011 Naslov: |
    |
|
|
[quote="pandora"]
a kako je [tex] dim L = dim M [/tex] zakljucujemo da je [tex] M = L = M \cap L [/tex].
meni nije jasan ovaj korak
zašto zaključujemo M=L ?[/quote]
Mislim da je to zato što smo zaključili da se baza za M može prikazati preko baze za L i k tome obe baze imaju jednak broj članova (tj.dimenzije M i L su jednake), dakle linearna ljuska baze za M = linearna ljuska baze za L. Iz toga slijedi da je M = L. Bar sam ja to pohvatala (jer postoje potprostori jednake dimenzije, a koji nisu međusobno jednaki, npr. prostori gornje- i donjetrokutastih matrica, ali u tom slučaju se baza prvog prostora ne može prikazati preko baze drugog, pa to nisu dva ista potprostora).
Ako pitaš i za drugi dio, to ti je ovo: Ako je M=L, tada umjesto [tex]M \cap L [/tex] možeš pisati [tex]M \cap M [/tex], odnosno M (presjek skupa sa samim sobom je opet taj skup).
| pandora (napisa): |
a kako je [tex] dim L = dim M [/tex] zakljucujemo da je [tex] M = L = M \cap L [/tex].
meni nije jasan ovaj korak
zašto zaključujemo M=L ? |
Mislim da je to zato što smo zaključili da se baza za M može prikazati preko baze za L i k tome obe baze imaju jednak broj članova (tj.dimenzije M i L su jednake), dakle linearna ljuska baze za M = linearna ljuska baze za L. Iz toga slijedi da je M = L. Bar sam ja to pohvatala (jer postoje potprostori jednake dimenzije, a koji nisu međusobno jednaki, npr. prostori gornje- i donjetrokutastih matrica, ali u tom slučaju se baza prvog prostora ne može prikazati preko baze drugog, pa to nisu dva ista potprostora).
Ako pitaš i za drugi dio, to ti je ovo: Ako je M=L, tada umjesto [tex]M \cap L [/tex] možeš pisati [tex]M \cap M [/tex], odnosno M (presjek skupa sa samim sobom je opet taj skup).
|
|
| [Vrh] |
|
bucko
Forumaš(ica)


Pridružen/a: 04. 12. 2007. (20:55:30)
Postovi: (A9)16
Spol: 
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
 Postano: 10:01 ned, 6. 11. 2011 Naslov: Postano: 10:01 ned, 6. 11. 2011 Naslov: |
    |
|
|
[quote="ceps"]Znači, [latex]M = \{x = (x_1, ... , x_{2n}) \in \mathbb{R}^{2n}| x_i +2x_{i+n} = 0, i = 1, ... , n\}[/latex]
Nemoj da te ovo zbuni sa 2n, to znači da gledamo prostore parne dimenzije.
Pa ajmo uzet nekoliko manjih takvih npr.
za [latex]\mathbb{R}^4[/latex]
To bi bili svi oni [latex](x_1, x_2, x_3, x_4)[/latex] za koje vrijedi:
[latex]x_1 + 2x_3 = 0[/latex]
[latex]x_2 + 2x_4 = 0[/latex]
to, jest
[latex]x_1 = -2x_3[/latex]
[latex]x_2 = -2x_4[/latex]
Znači, bili bi oblika
[latex](-2x_3, -2x_4, x_2, x_4)[/latex] - jedna baza za takve članove R-4 bi bila
[latex](-2, 0, 1, 0) , (0, -2, 0, 1)[/latex] i M bi bio 2dimenzionalan.
Ako ti nije jasno kako bi sad to generalizirao na R-2n, probaj si još napraviti za R-6, recimo, pa možda vidiš uzorak! :)[/quote]
a možeš to probat raspisat za 2-ntorku jer mi to nije jasno :/
| ceps (napisa): | Znači, 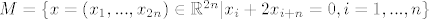
Nemoj da te ovo zbuni sa 2n, to znači da gledamo prostore parne dimenzije.
Pa ajmo uzet nekoliko manjih takvih npr.
za 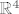
To bi bili svi oni 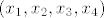 za koje vrijedi: za koje vrijedi:
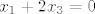
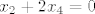
to, jest
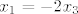
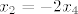
Znači, bili bi oblika
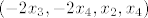 - jedna baza za takve članove R-4 bi bila - jedna baza za takve članove R-4 bi bila
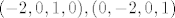 i M bi bio 2dimenzionalan. i M bi bio 2dimenzionalan.
Ako ti nije jasno kako bi sad to generalizirao na R-2n, probaj si još napraviti za R-6, recimo, pa možda vidiš uzorak!  |
a možeš to probat raspisat za 2-ntorku jer mi to nije jasno 
|
|
| [Vrh] |
|
pandora
Forumaš(ica)

Pridružen/a: 22. 10. 2011. (16:55:23)
Postovi: (1A)16
|
 Postano: 10:19 ned, 6. 11. 2011 Naslov: Postano: 10:19 ned, 6. 11. 2011 Naslov: |
    |
|
|
[quote="PermutiranoPrase"][quote="pandora"]
a kako je [tex] dim L = dim M [/tex] zakljucujemo da je [tex] M = L = M \cap L [/tex].
meni nije jasan ovaj korak
zašto zaključujemo M=L ?[/quote]
Mislim da je to zato što smo zaključili da se baza za M može prikazati preko baze za L i k tome obe baze imaju jednak broj članova (tj.dimenzije M i L su jednake), dakle linearna ljuska baze za M = linearna ljuska baze za L. Iz toga slijedi da je M = L. Bar sam ja to pohvatala (jer postoje potprostori jednake dimenzije, a koji nisu međusobno jednaki, npr. prostori gornje- i donjetrokutastih matrica, ali u tom slučaju se baza prvog prostora ne može prikazati preko baze drugog, pa to nisu dva ista potprostora).
Ako pitaš i za drugi dio, to ti je ovo: Ako je M=L, tada umjesto [tex]M \cap L [/tex] možeš pisati [tex]M \cap M [/tex], odnosno M (presjek skupa sa samim sobom je opet taj skup).[/quote]
ajme, puno ti hvala, sad mi je puno jasnije
| PermutiranoPrase (napisa): | | pandora (napisa): |
a kako je [tex] dim L = dim M [/tex] zakljucujemo da je [tex] M = L = M \cap L [/tex].
meni nije jasan ovaj korak
zašto zaključujemo M=L ? |
Mislim da je to zato što smo zaključili da se baza za M može prikazati preko baze za L i k tome obe baze imaju jednak broj članova (tj.dimenzije M i L su jednake), dakle linearna ljuska baze za M = linearna ljuska baze za L. Iz toga slijedi da je M = L. Bar sam ja to pohvatala (jer postoje potprostori jednake dimenzije, a koji nisu međusobno jednaki, npr. prostori gornje- i donjetrokutastih matrica, ali u tom slučaju se baza prvog prostora ne može prikazati preko baze drugog, pa to nisu dva ista potprostora).
Ako pitaš i za drugi dio, to ti je ovo: Ako je M=L, tada umjesto [tex]M \cap L [/tex] možeš pisati [tex]M \cap M [/tex], odnosno M (presjek skupa sa samim sobom je opet taj skup). |
ajme, puno ti hvala, sad mi je puno jasnije
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 10:42 ned, 6. 11. 2011 Naslov: Postano: 10:42 ned, 6. 11. 2011 Naslov: |
    |
|
|
[quote="pedro"][quote="ceps"]Znači, [latex]M = \{x = (x_1, ... , x_{2n}) \in \mathbb{R}^{2n}| x_i +2x_{i+n} = 0, i = 1, ... , n\}[/latex]
Nemoj da te ovo zbuni sa 2n, to znači da gledamo prostore parne dimenzije.
Pa ajmo uzet nekoliko manjih takvih npr.
za [latex]\mathbb{R}^4[/latex]
To bi bili svi oni [latex](x_1, x_2, x_3, x_4)[/latex] za koje vrijedi:
[latex]x_1 + 2x_3 = 0[/latex]
[latex]x_2 + 2x_4 = 0[/latex]
to, jest
[latex]x_1 = -2x_3[/latex]
[latex]x_2 = -2x_4[/latex]
Znači, bili bi oblika
[latex](-2x_3, -2x_4, x_2, x_4)[/latex] - jedna baza za takve članove R-4 bi bila
[latex](-2, 0, 1, 0) , (0, -2, 0, 1)[/latex] i M bi bio 2dimenzionalan.
Ako ti nije jasno kako bi sad to generalizirao na R-2n, probaj si još napraviti za R-6, recimo, pa možda vidiš uzorak! :)[/quote]
a možeš to probat raspisat za 2-ntorku jer mi to nije jasno :/[/quote]
A što ti točno nije jasno?
Za [latex]\mathbb{R}^6[/latex] bi bilo:
[latex]x_1 = -2x_3[/latex]
[latex]x_2 = -2x_4[/latex]
[latex]x_3 = -2x_6[/latex]
pa bi baza bila [latex](-2, 0, 0, 1, 0, 0), (0, -2, 0, 0, 1, 0), (0, 0, -2, 0, 0, 1)[/latex]
Prva 3 iksa su određena preko zadnja 3, dimenzija je 3... kao što vidiš.
Uz istu argumentaciju za [latex]\mathbb{R}^{2n}[/latex] bi imao prvih n ikseva određenih preko zadnjih n... dimenziju n.
A bazu je teško malo ovako zapisati, ni Tex mi ne pomaže, ali vidiš oblik iz primjera za 4 i 6 dimenzija:
-2 na 1. mjestu, na n-tom mjestu 1, sve ostalo nule
-2 na 2. mjestu, na n+1 mjestu 1, sve ostalo nule
.
.
.
-2 na ntom mjestu, na 2ntom mjestu 1, sve ostalo nule
| pedro (napisa): | | ceps (napisa): | Znači, 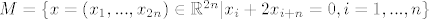
Nemoj da te ovo zbuni sa 2n, to znači da gledamo prostore parne dimenzije.
Pa ajmo uzet nekoliko manjih takvih npr.
za 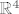
To bi bili svi oni 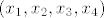 za koje vrijedi: za koje vrijedi:
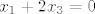
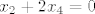
to, jest
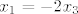
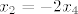
Znači, bili bi oblika
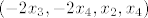 - jedna baza za takve članove R-4 bi bila - jedna baza za takve članove R-4 bi bila
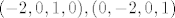 i M bi bio 2dimenzionalan. i M bi bio 2dimenzionalan.
Ako ti nije jasno kako bi sad to generalizirao na R-2n, probaj si još napraviti za R-6, recimo, pa možda vidiš uzorak!  |
a možeš to probat raspisat za 2-ntorku jer mi to nije jasno  |
A što ti točno nije jasno?
Za 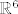 bi bilo: bi bilo:
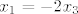
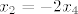
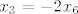
pa bi baza bila 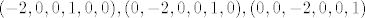
Prva 3 iksa su određena preko zadnja 3, dimenzija je 3... kao što vidiš.
Uz istu argumentaciju za 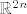 bi imao prvih n ikseva određenih preko zadnjih n... dimenziju n. bi imao prvih n ikseva određenih preko zadnjih n... dimenziju n.
A bazu je teško malo ovako zapisati, ni Tex mi ne pomaže, ali vidiš oblik iz primjera za 4 i 6 dimenzija:
-2 na 1. mjestu, na n-tom mjestu 1, sve ostalo nule
-2 na 2. mjestu, na n+1 mjestu 1, sve ostalo nule
.
.
.
-2 na ntom mjestu, na 2ntom mjestu 1, sve ostalo nule
|
|
| [Vrh] |
|
miss.zohar
Forumaš(ica)

Pridružen/a: 01. 11. 2011. (20:47:40)
Postovi: (A)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
 Postano: 10:57 ned, 6. 11. 2011 Naslov: Postano: 10:57 ned, 6. 11. 2011 Naslov: |
    |
|
|
[quote="ceps"][quote="pedro"][quote="ceps"]Znači, [latex]M = \{x = (x_1, ... , x_{2n}) \in \mathbb{R}^{2n}| x_i +2x_{i+n} = 0, i = 1, ... , n\}[/latex]
Nemoj da te ovo zbuni sa 2n, to znači da gledamo prostore parne dimenzije.
Pa ajmo uzet nekoliko manjih takvih npr.
za [latex]\mathbb{R}^4[/latex]
To bi bili svi oni [latex](x_1, x_2, x_3, x_4)[/latex] za koje vrijedi:
[latex]x_1 + 2x_3 = 0[/latex]
[latex]x_2 + 2x_4 = 0[/latex]
to, jest
[latex]x_1 = -2x_3[/latex]
[latex]x_2 = -2x_4[/latex]
Znači, bili bi oblika
[latex](-2x_3, -2x_4, x_2, x_4)[/latex] - jedna baza za takve članove R-4 bi bila
[latex](-2, 0, 1, 0) , (0, -2, 0, 1)[/latex] i M bi bio 2dimenzionalan.
Ako ti nije jasno kako bi sad to generalizirao na R-2n, probaj si još napraviti za R-6, recimo, pa možda vidiš uzorak! :)[/quote]
a možeš to probat raspisat za 2-ntorku jer mi to nije jasno :/[/quote]
A što ti točno nije jasno?
Za [latex]\mathbb{R}^6[/latex] bi bilo:
[latex]x_1 = -2x_3[/latex]
[latex]x_2 = -2x_4[/latex]
[latex]x_3 = -2x_6[/latex]
pa bi baza bila [latex](-2, 0, 0, 1, 0, 0), (0, -2, 0, 0, 1, 0), (0, 0, -2, 0, 0, 1)[/latex]
Prva 3 iksa su određena preko zadnja 3, dimenzija je 3... kao što vidiš.
Uz istu argumentaciju za [latex]\mathbb{R}^{2n}[/latex] bi imao prvih n ikseva određenih preko zadnjih n... dimenziju n.
A bazu je teško malo ovako zapisati, ni Tex mi ne pomaže, ali vidiš oblik iz primjera za 4 i 6 dimenzija:
[b]-2 na 1. mjestu, na n-tom mjestu 1, sve ostalo nule
-2 na 2. mjestu, na n+1 mjestu 1, sve ostalo nule
.
.
.
-2 na ntom mjestu, na 2ntom mjestu 1, sve ostalo nule[/b][/quote]
hmmm...kaj nije ovak(možda se varam):
-2 na 1. mjestu, na n+1-vom mjestu 1, sve ostalo nule
-2 na 2. mjestu, na n+2 mjestu 1, sve ostalo nule
.
.
.
-2 na ntom mjestu, na 2ntom mjestu 1, sve ostalo nule
| ceps (napisa): | | pedro (napisa): | | ceps (napisa): | Znači, 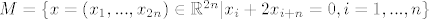
Nemoj da te ovo zbuni sa 2n, to znači da gledamo prostore parne dimenzije.
Pa ajmo uzet nekoliko manjih takvih npr.
za 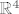
To bi bili svi oni 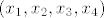 za koje vrijedi: za koje vrijedi:
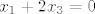
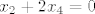
to, jest
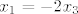
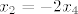
Znači, bili bi oblika
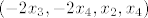 - jedna baza za takve članove R-4 bi bila - jedna baza za takve članove R-4 bi bila
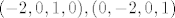 i M bi bio 2dimenzionalan. i M bi bio 2dimenzionalan.
Ako ti nije jasno kako bi sad to generalizirao na R-2n, probaj si još napraviti za R-6, recimo, pa možda vidiš uzorak!  |
a možeš to probat raspisat za 2-ntorku jer mi to nije jasno  |
A što ti točno nije jasno?
Za 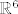 bi bilo: bi bilo:
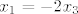
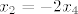
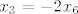
pa bi baza bila 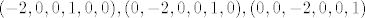
Prva 3 iksa su određena preko zadnja 3, dimenzija je 3... kao što vidiš.
Uz istu argumentaciju za 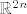 bi imao prvih n ikseva određenih preko zadnjih n... dimenziju n. bi imao prvih n ikseva određenih preko zadnjih n... dimenziju n.
A bazu je teško malo ovako zapisati, ni Tex mi ne pomaže, ali vidiš oblik iz primjera za 4 i 6 dimenzija:
-2 na 1. mjestu, na n-tom mjestu 1, sve ostalo nule
-2 na 2. mjestu, na n+1 mjestu 1, sve ostalo nule
.
.
.
-2 na ntom mjestu, na 2ntom mjestu 1, sve ostalo nule |
hmmm...kaj nije ovak(možda se varam):
-2 na 1. mjestu, na n+1-vom mjestu 1, sve ostalo nule
-2 na 2. mjestu, na n+2 mjestu 1, sve ostalo nule
.
.
.
-2 na ntom mjestu, na 2ntom mjestu 1, sve ostalo nule
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
logikaus
Forumaš(ica)

Pridružen/a: 12. 10. 2011. (17:55:23)
Postovi: (45)16
|
 Postano: 11:30 ned, 6. 11. 2011 Naslov: Postano: 11:30 ned, 6. 11. 2011 Naslov: |
    |
|
|
evo, imam ja jos jedno pitanje vezano uz zadatak s vjezbi
a1=(1,1,2,2)
b1=(1,0,0,1)
a2=(2,1,2,3)
b2=(0,1,2,1)
neka je M1=[{a1,b1}]
M2=[{a2,b2}]
gokažite da je m1=m2
e to znaci da moramo pokazati da je m1 podskup od m2 i obrnuto...
on je za m1 podskup m2 napravio ove cetiri jednadzbe
2A = 1
A + B =1
2A + 2B = 2
3A + B =2 ...OD KUD MU TO, KAJ JE IZJEDNACIO S CIM? -.- =)
evo, imam ja jos jedno pitanje vezano uz zadatak s vjezbi
a1=(1,1,2,2)
b1=(1,0,0,1)
a2=(2,1,2,3)
b2=(0,1,2,1)
neka je M1=[{a1,b1}]
M2=[{a2,b2}]
gokažite da je m1=m2
e to znaci da moramo pokazati da je m1 podskup od m2 i obrnuto...
on je za m1 podskup m2 napravio ove cetiri jednadzbe
2A = 1
A + B =1
2A + 2B = 2
3A + B =2 ...OD KUD MU TO, KAJ JE IZJEDNACIO S CIM? -.- =)
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 12:07 ned, 6. 11. 2011 Naslov: Postano: 12:07 ned, 6. 11. 2011 Naslov: |
    |
|
|
Pošto mogu čitati misli asistenata, mislim da je išao prikazati [latex]a_1[/latex] sa [latex]a_2[/latex] i [latex]b_2[/latex] kao:
[latex]a_1 = A\cdot a_2 + B \cdot b_2[/latex]
[latex](1,1,2,2) = (2A, A, 2A, 3A) + (0, B, 2B, B)[/latex]
[latex](1,1,2,2) = (2A, A + B, 2A + 2B, 3A + B)[/latex]
(gdje su A i B iz R-a)
Evo misterioznih jednadžbi! :)
Ne shvaćam je li i dio pitanja ZAŠTO je to napravio... ako je samo reci, mogu napisat još malo. :)
Pošto mogu čitati misli asistenata, mislim da je išao prikazati 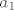 sa sa 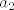 i i 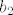 kao: kao:
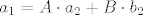
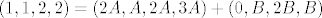
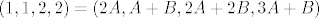
(gdje su A i B iz R-a)
Evo misterioznih jednadžbi! 
Ne shvaćam je li i dio pitanja ZAŠTO je to napravio... ako je samo reci, mogu napisat još malo. 
|
|
| [Vrh] |
|
pandora
Forumaš(ica)

Pridružen/a: 22. 10. 2011. (16:55:23)
Postovi: (1A)16
|
 Postano: 12:43 ned, 6. 11. 2011 Naslov: Postano: 12:43 ned, 6. 11. 2011 Naslov: |
    |
|
|
[quote="pedro"][quote="ceps"][quote="pedro"][quote="ceps"]Znači, [latex]M = \{x = (x_1, ... , x_{2n}) \in \mathbb{R}^{2n}| x_i +2x_{i+n} = 0, i = 1, ... , n\}[/latex]
Nemoj da te ovo zbuni sa 2n, to znači da gledamo prostore parne dimenzije.
Pa ajmo uzet nekoliko manjih takvih npr.
za [latex]\mathbb{R}^4[/latex]
To bi bili svi oni [latex](x_1, x_2, x_3, x_4)[/latex] za koje vrijedi:
[latex]x_1 + 2x_3 = 0[/latex]
[latex]x_2 + 2x_4 = 0[/latex]
to, jest
[latex]x_1 = -2x_3[/latex]
[latex]x_2 = -2x_4[/latex]
Znači, bili bi oblika
[latex](-2x_3, -2x_4, x_2, x_4)[/latex] - jedna baza za takve članove R-4 bi bila
[latex](-2, 0, 1, 0) , (0, -2, 0, 1)[/latex] i M bi bio 2dimenzionalan.
Ako ti nije jasno kako bi sad to generalizirao na R-2n, probaj si još napraviti za R-6, recimo, pa možda vidiš uzorak! :)[/quote]
a možeš to probat raspisat za 2-ntorku jer mi to nije jasno :/[/quote]
A što ti točno nije jasno?
Za [latex]\mathbb{R}^6[/latex] bi bilo:
[latex]x_1 = -2x_3[/latex]
[latex]x_2 = -2x_4[/latex]
[latex]x_3 = -2x_6[/latex]
pa bi baza bila [latex](-2, 0, 0, 1, 0, 0), (0, -2, 0, 0, 1, 0), (0, 0, -2, 0, 0, 1)[/latex]
Prva 3 iksa su određena preko zadnja 3, dimenzija je 3... kao što vidiš.
Uz istu argumentaciju za [latex]\mathbb{R}^{2n}[/latex] bi imao prvih n ikseva određenih preko zadnjih n... dimenziju n.
A bazu je teško malo ovako zapisati, ni Tex mi ne pomaže, ali vidiš oblik iz primjera za 4 i 6 dimenzija:
[b]-2 na 1. mjestu, na n-tom mjestu 1, sve ostalo nule
-2 na 2. mjestu, na n+1 mjestu 1, sve ostalo nule
.
.
.
-2 na ntom mjestu, na 2ntom mjestu 1, sve ostalo nule[/b][/quote]
hmmm...kaj nije ovak(možda se varam):
-2 na 1. mjestu, na n+1-vom mjestu 1, sve ostalo nule
-2 na 2. mjestu, na n+2 mjestu 1, sve ostalo nule
.
.
.
-2 na ntom mjestu, na 2ntom mjestu 1, sve ostalo nule[/quote]
u prvoj grupi u tom zadatku dan je prostor neparne dimenzije [latex]\mathbb{R}^{2n+1}[/latex]
nakon što uzmem za npr, R3 ili R5 dobivam
[latex](1, 0, -2), (0, 1, 0) [/latex] baza za članove R3
[latex](1, 0, 0, -2, 0), (0, 1, 0, 0, -2), (0, 0, 1, 0, 0) [/latex] baza za članove R5
je li onda konačno rješenje oblika:
1 na 1.mjestu, -2 na n+2 mjestu, ostalo 0
1 na 2.mjestu, -2 na n+3 mjestu, ostalo 0
.
.
.
1 n-tom mjestu, -2 na 2n-tom mjestu, ostalo 0 i još na kraju na 1 na n+1 mjestu ostalo 0?
| pedro (napisa): | | ceps (napisa): | | pedro (napisa): | | ceps (napisa): | Znači, 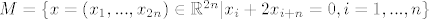
Nemoj da te ovo zbuni sa 2n, to znači da gledamo prostore parne dimenzije.
Pa ajmo uzet nekoliko manjih takvih npr.
za 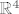
To bi bili svi oni 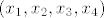 za koje vrijedi: za koje vrijedi:
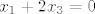
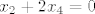
to, jest
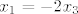
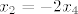
Znači, bili bi oblika
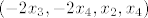 - jedna baza za takve članove R-4 bi bila - jedna baza za takve članove R-4 bi bila
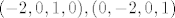 i M bi bio 2dimenzionalan. i M bi bio 2dimenzionalan.
Ako ti nije jasno kako bi sad to generalizirao na R-2n, probaj si još napraviti za R-6, recimo, pa možda vidiš uzorak!  |
a možeš to probat raspisat za 2-ntorku jer mi to nije jasno  |
A što ti točno nije jasno?
Za 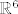 bi bilo: bi bilo:
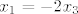
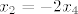
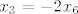
pa bi baza bila 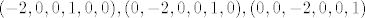
Prva 3 iksa su određena preko zadnja 3, dimenzija je 3... kao što vidiš.
Uz istu argumentaciju za 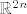 bi imao prvih n ikseva određenih preko zadnjih n... dimenziju n. bi imao prvih n ikseva određenih preko zadnjih n... dimenziju n.
A bazu je teško malo ovako zapisati, ni Tex mi ne pomaže, ali vidiš oblik iz primjera za 4 i 6 dimenzija:
-2 na 1. mjestu, na n-tom mjestu 1, sve ostalo nule
-2 na 2. mjestu, na n+1 mjestu 1, sve ostalo nule
.
.
.
-2 na ntom mjestu, na 2ntom mjestu 1, sve ostalo nule |
hmmm...kaj nije ovak(možda se varam):
-2 na 1. mjestu, na n+1-vom mjestu 1, sve ostalo nule
-2 na 2. mjestu, na n+2 mjestu 1, sve ostalo nule
.
.
.
-2 na ntom mjestu, na 2ntom mjestu 1, sve ostalo nule |
u prvoj grupi u tom zadatku dan je prostor neparne dimenzije 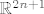
nakon što uzmem za npr, R3 ili R5 dobivam
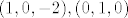 baza za članove R3 baza za članove R3
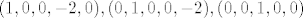 baza za članove R5 baza za članove R5
je li onda konačno rješenje oblika:
1 na 1.mjestu, -2 na n+2 mjestu, ostalo 0
1 na 2.mjestu, -2 na n+3 mjestu, ostalo 0
.
.
.
1 n-tom mjestu, -2 na 2n-tom mjestu, ostalo 0 i još na kraju na 1 na n+1 mjestu ostalo 0?
|
|
| [Vrh] |
|
Sino
Forumaš(ica)


Pridružen/a: 06. 10. 2011. (14:09:58)
Postovi: (14)16
Spol: 
|
 Postano: 14:20 ned, 6. 11. 2011 Naslov: Postano: 14:20 ned, 6. 11. 2011 Naslov: |
    |
|
|
[quote="helga"]
Nego, ako je tkogod riješio 2.B - je li baza za
[b](M+L) ∩ K -> {(1,1,1,1), (1,2,1,2)}[/b][/quote]
I ja sam dobio takvo rješenje
| helga (napisa): |
Nego, ako je tkogod riješio 2.B - je li baza za
(M+L) ∩ K → {(1,1,1,1), (1,2,1,2)} |
I ja sam dobio takvo rješenje
|
|
| [Vrh] |
|
pandora
Forumaš(ica)

Pridružen/a: 22. 10. 2011. (16:55:23)
Postovi: (1A)16
|
 Postano: 14:51 ned, 6. 11. 2011 Naslov: Postano: 14:51 ned, 6. 11. 2011 Naslov: |
    |
|
|
[quote="Sino"][quote="helga"]
Nego, ako je tkogod riješio 2.B - je li baza za
[b](M+L) ∩ K -> {(1,1,1,1), (1,2,1,2)}[/b][/quote]
I ja sam dobio takvo rješenje[/quote]
Moze postupak? :/
| Sino (napisa): | | helga (napisa): |
Nego, ako je tkogod riješio 2.B - je li baza za
(M+L) ∩ K → {(1,1,1,1), (1,2,1,2)} |
I ja sam dobio takvo rješenje |
Moze postupak? 
|
|
| [Vrh] |
|
logikaus
Forumaš(ica)

Pridružen/a: 12. 10. 2011. (17:55:23)
Postovi: (45)16
|
 Postano: 19:30 ned, 6. 11. 2011 Naslov: Postano: 19:30 ned, 6. 11. 2011 Naslov: |
    |
|
|
[quote="ceps"]Pošto mogu čitati misli asistenata, mislim da je išao prikazati [latex]a_1[/latex] sa [latex]a_2[/latex] i [latex]b_2[/latex] kao:
[latex]a_1 = A\cdot a_2 + B \cdot b_2[/latex]
[latex](1,1,2,2) = (2A, A, 2A, 3A) + (0, B, 2B, B)[/latex]
[latex](1,1,2,2) = (2A, A + B, 2A + 2B, 3A + B)[/latex]
(gdje su A i B iz R-a)
Evo misterioznih jednadžbi! :)
Ne shvaćam je li i dio pitanja ZAŠTO je to napravio... ako je samo reci, mogu napisat još malo. :)[/quote]
ee ma to mi je trabalo =) tj. i mislila sam da ide ta formula al sam nesto krivo uvrstila i nikak nisam mogla dobiti tocno rjesenje ^^
hvala
| ceps (napisa): | Pošto mogu čitati misli asistenata, mislim da je išao prikazati 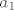 sa sa 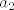 i i 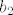 kao: kao:
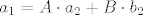
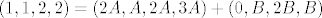
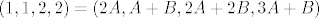
(gdje su A i B iz R-a)
Evo misterioznih jednadžbi! 
Ne shvaćam je li i dio pitanja ZAŠTO je to napravio... ako je samo reci, mogu napisat još malo.  |
ee ma to mi je trabalo =) tj. i mislila sam da ide ta formula al sam nesto krivo uvrstila i nikak nisam mogla dobiti tocno rjesenje ^^
hvala
|
|
| [Vrh] |
|
|










