| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
mini
Forumaš(ica)
Pridružen/a: 04. 02. 2009. (14:31:34)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
matijaB
Forumaš(ica)

Pridružen/a: 19. 08. 2010. (09:11:43)
Postovi: (4D)16
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
 Postano: 23:42 pon, 7. 11. 2011 Naslov: Postano: 23:42 pon, 7. 11. 2011 Naslov: |
    |
|
|
[quote="matijaB"]da bi poceli igrati igru,treba nam 6 na kocki. Nakon koliko bacanja kocke bi vjerojatnost da je pala 6 bila barem 0.95 ?[/quote]
Vjerojatnost da u [tex]k[/tex] bacanja nijednom ne padne 6 iznosi [tex](5/6)^k[/tex]. Sad tražiš najmanji [tex]k[/tex] za koji je [tex](5/6)^k \le 0.05[/tex]. Za takav [tex]k[/tex], vjerojatnost da se dogodi komplementarni događaj - tj. da padne barem jedna šestica - je [tex]\geq 0.95[/tex].
[size=9][color=#999999]Added after 24 minutes:[/color][/size]
[quote="ceps"]Koji te dio točno muči?
Imaš tri događaja
A = {zbroj brojeva na kockama je 25}
B = {bar jednom padne 5}
C = {produkt dobivenih brojeva je djeljiv sa 10}
Trebaš izračunati P(A U B U C), tako da će ti trebati i vjerojatnosti događaja A presjek B, A presjek C, B presjek C i A presjek B presjek C...
Vidiš da tu ima dosta računanja, pa mi se ne da sad sve baš pisati... xD
[/quote]
Evo ja ću ovo dovršiti.
Primijetimo da je [tex]C\subseteq B[/tex] (ako je produkt djeljiv s [tex]10[/tex], sigurno je pala petica) pa možemo pojednostavniti stvar: [tex]P(A \cup B \cup C) = P(A \cup B)[/tex].
E to ćemo pak ovako: [tex]P(A \cup B) = P(A\setminus B) + P(B)[/tex], tu varijantu sam odabrao jer ove desno znam izračunati.
Ok, [tex]P(B) = 1-P(B^c)[/tex], a vjerojatnost da nijednom ne padne petica je [tex](5/6)^5[/tex], pa je [tex]P(B) = 1-(5/6)^5[/tex].
Sad pogledajmo [tex]P(A\setminus B)[/tex]. To su događaji kad je zbroj bio jednak [tex]25[/tex], ali nije pala petica. Fora je što tih događaja ima relativno malo. To su:
[tex]6,6,6,6,1[/tex] - ukupno [tex]5[/tex] permutacija (biramo gdje ćemo staviti jedinicu)
[tex]6,6,6,4,3[/tex] - ukupno [tex]20[/tex] permutacija (biramo gdje ćemo staviti četvorku, pa onda gdje ćemo staviti trojku, dakle [tex]5\cdot 4[/tex])
Dakle [tex]P(A\setminus B) = \displaystyle\frac{5+20}{6^5} = \frac{1}{6^3}[/tex]. Konačno rješenje bilo bi dakle [tex]1-\displaystyle\bigg(\frac{5}{6}\bigg)^5+\frac{1}{6^3}[/tex].
| matijaB (napisa): | | da bi poceli igrati igru,treba nam 6 na kocki. Nakon koliko bacanja kocke bi vjerojatnost da je pala 6 bila barem 0.95 ? |
Vjerojatnost da u [tex]k[/tex] bacanja nijednom ne padne 6 iznosi [tex](5/6)^k[/tex]. Sad tražiš najmanji [tex]k[/tex] za koji je [tex](5/6)^k \le 0.05[/tex]. Za takav [tex]k[/tex], vjerojatnost da se dogodi komplementarni događaj - tj. da padne barem jedna šestica - je [tex]\geq 0.95[/tex].
Added after 24 minutes:
| ceps (napisa): | Koji te dio točno muči?
Imaš tri događaja
A = {zbroj brojeva na kockama je 25}
B = {bar jednom padne 5}
C = {produkt dobivenih brojeva je djeljiv sa 10}
Trebaš izračunati P(A U B U C), tako da će ti trebati i vjerojatnosti događaja A presjek B, A presjek C, B presjek C i A presjek B presjek C...
Vidiš da tu ima dosta računanja, pa mi se ne da sad sve baš pisati... xD
|
Evo ja ću ovo dovršiti.
Primijetimo da je [tex]C\subseteq B[/tex] (ako je produkt djeljiv s [tex]10[/tex], sigurno je pala petica) pa možemo pojednostavniti stvar: [tex]P(A \cup B \cup C) = P(A \cup B)[/tex].
E to ćemo pak ovako: [tex]P(A \cup B) = P(A\setminus B) + P(B)[/tex], tu varijantu sam odabrao jer ove desno znam izračunati.
Ok, [tex]P(B) = 1-P(B^c)[/tex], a vjerojatnost da nijednom ne padne petica je [tex](5/6)^5[/tex], pa je [tex]P(B) = 1-(5/6)^5[/tex].
Sad pogledajmo [tex]P(A\setminus B)[/tex]. To su događaji kad je zbroj bio jednak [tex]25[/tex], ali nije pala petica. Fora je što tih događaja ima relativno malo. To su:
[tex]6,6,6,6,1[/tex] - ukupno [tex]5[/tex] permutacija (biramo gdje ćemo staviti jedinicu)
[tex]6,6,6,4,3[/tex] - ukupno [tex]20[/tex] permutacija (biramo gdje ćemo staviti četvorku, pa onda gdje ćemo staviti trojku, dakle [tex]5\cdot 4[/tex])
Dakle [tex]P(A\setminus B) = \displaystyle\frac{5+20}{6^5} = \frac{1}{6^3}[/tex]. Konačno rješenje bilo bi dakle [tex]1-\displaystyle\bigg(\frac{5}{6}\bigg)^5+\frac{1}{6^3}[/tex].
|
|
| [Vrh] |
|
tinky
Forumaš(ica)
Pridružen/a: 20. 06. 2008. (11:59:08)
Postovi: (3F)16
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
 Postano: 12:40 uto, 8. 11. 2011 Naslov: Postano: 12:40 uto, 8. 11. 2011 Naslov: |
    |
|
|
[quote="tinky"]Moze netko rijesiti zadatak 2. iz prvog kolokvija 2007 god. u obe grupe?[/quote]
A grupa.
2.a) Međusobnim oduzimanjem zadanih skupova [tex]A_n[/tex] zaključujemo da naša [tex]\sigma[/tex]-algebra mora sadržavati sve skupove oblika [tex](k, k+1][/tex] za [tex]1\le k\le 4[/tex], a također i skup [tex](5,10][/tex] kao komplement od [tex][0,5][/tex]. Navedeni skupovi, zajedno sa [tex][0,1][/tex], međusobno su disjunktni i "nedjeljivi" pa možemo zaključiti su to atomi naše [tex]\sigma[/tex]-algebre:
[tex]\delta = \{[0,1], (1,2],(2,3],(3,4],(4,5],(5,10]\}[/tex]
To znači da je svaki skup iz [tex]\sigma[/tex]-algebre sastavljen kao unija nekih od ovih atoma. Dakle naša [tex]\sigma[/tex]-algebra sadrži [tex]2^6[/tex] skupova.
2.b) Po definiciji, tražimo [tex]\lim\sup B_n=\displaystyle \bigcap_{n=1}^\infty \bigcup_{k=n}^\infty B_k[/tex]. Fiksirajmo [tex]n[/tex] i pogledajmo čemu je jednaka unija:
[tex]\displaystyle\bigcup_{k=n}^\infty B_k = \bigcup_{k=n}^\infty\bigg[\frac 1 k, 5+\frac 1 k\bigg] = \bigg(0, 5+\frac 1 n\bigg][/tex], pa konačno imamo [tex]\lim\sup B_n = \displaystyle \bigcap_{n=1}^\infty \bigg(0, 5+\frac 1 n\bigg] = (0, 5][/tex].
Druga grupa se rješava slično.
| tinky (napisa): | | Moze netko rijesiti zadatak 2. iz prvog kolokvija 2007 god. u obe grupe? |
A grupa.
2.a) Međusobnim oduzimanjem zadanih skupova [tex]A_n[/tex] zaključujemo da naša [tex]\sigma[/tex]-algebra mora sadržavati sve skupove oblika [tex](k, k+1][/tex] za [tex]1\le k\le 4[/tex], a također i skup [tex](5,10][/tex] kao komplement od [tex][0,5][/tex]. Navedeni skupovi, zajedno sa [tex][0,1][/tex], međusobno su disjunktni i "nedjeljivi" pa možemo zaključiti su to atomi naše [tex]\sigma[/tex]-algebre:
[tex]\delta = \{[0,1], (1,2],(2,3],(3,4],(4,5],(5,10]\}[/tex]
To znači da je svaki skup iz [tex]\sigma[/tex]-algebre sastavljen kao unija nekih od ovih atoma. Dakle naša [tex]\sigma[/tex]-algebra sadrži [tex]2^6[/tex] skupova.
2.b) Po definiciji, tražimo [tex]\lim\sup B_n=\displaystyle \bigcap_{n=1}^\infty \bigcup_{k=n}^\infty B_k[/tex]. Fiksirajmo [tex]n[/tex] i pogledajmo čemu je jednaka unija:
[tex]\displaystyle\bigcup_{k=n}^\infty B_k = \bigcup_{k=n}^\infty\bigg[\frac 1 k, 5+\frac 1 k\bigg] = \bigg(0, 5+\frac 1 n\bigg][/tex], pa konačno imamo [tex]\lim\sup B_n = \displaystyle \bigcap_{n=1}^\infty \bigg(0, 5+\frac 1 n\bigg] = (0, 5][/tex].
Druga grupa se rješava slično.
|
|
| [Vrh] |
|
tinky
Forumaš(ica)
Pridružen/a: 20. 06. 2008. (11:59:08)
Postovi: (3F)16
|
|
| [Vrh] |
|
Stuart
Forumaš(ica)

Pridružen/a: 11. 01. 2011. (16:42:01)
Postovi: (9)16
|
|
| [Vrh] |
|
A_je_to
Forumaš(ica)

Pridružen/a: 19. 02. 2009. (16:51:22)
Postovi: (6D)16
Spol: 
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
 Postano: 17:30 uto, 8. 11. 2011 Naslov: Postano: 17:30 uto, 8. 11. 2011 Naslov: |
    |
|
|
[quote="A_je_to"]Kako se u 3.a) zadatku dobije ovaj P(Hi)? Unaprijed zahvaljujem:
http://web.math.hr/nastava/uuv/kolokviji/vjer-1011-kol1.pdf[/quote]
Jedinica u svakom bacanju pada s vjerojatnošću od [tex]1/6[/tex]. Vjerojatnost da jedinica padne točno [tex]i[/tex] puta iznosi [tex]{5 \choose i}(1/6)^i(5/6)^{5-i}[/tex]. Zašto?
Biramo na kojih [tex]i[/tex] kocaka (od ukupno [tex]5[/tex]) će pasti jedinica, to je [tex]{5\choose i}[/tex] događaja, ti događaji su disjunktni a vjerojatnost svakog od njih je [tex](1/6)^i[/tex] (vjerojatnost da na tih [tex]i[/tex] kocaka padne jedinica) puta [tex](5/6)^{5-i}[/tex] (vjerojatnost da na preostalih [tex]5-i[/tex] kocaka [i]ne[/i] padne jedinica).
[size=9][color=#999999]Added after 49 minutes:[/color][/size]
[quote="Stuart"]Može neki hint za 4. zadatak iz prve grupe?
http://web.math.hr/nastava/uuv/files/uuv-0708-kol1.pdf
Kao rješenje mi je ispalo 38/105, ali ne znam je li dobro.
Unaprijed hvala. :D[/quote]
Definirajmo potpun sistem događaja: [tex]H_k = [/tex] { u prvom izvlačenju dobili smo sumu [tex]k[/tex] }, za [tex]k=2,3,4[/tex]. [tex]P(H_k)[/tex] je lako izračunati.
Potom analogno definiramo [tex]A_k = [/tex] { u drugom izvlačenju dobili smo sumu [tex]k[/tex] }, za [tex]k=2,3,4[/tex].
Nas zanimaju događaji u kojima je suma jednaka, tj. kad se dogode [tex]H_k[/tex] i [tex]A_k[/tex]. Rješenje je dakle
[tex]P(A_2\cap H_2) + P(A_3\cap H_3) + P(A_4\cap H_4) = P(A_2 | H_2)P(H_2) + P(A_3 | H_3)P(H_3)+P(A_4 | H_4)P(H_4)[/tex],
što ne bi trebalo biti teško izračunati:
- za [tex]P(A_2 | H_2)[/tex] tražimo vjerojatnost da izvučemo dvije manje kovanice ako nam je ostalo 4 manje i 4 veće,
- za [tex]P(A_3 | H_3)[/tex] tražimo vjerojatnost da izvučemo jednu manju i jednu veću kovanicu ako nam je ostalo 5 manjih i 3 veće,
- za [tex]P(A_4 | H_4)[/tex] tražimo vjerojatnost da izvučemo dvije veće kovanice ako nam je ostalo 6 manjih i 2 veće.
Jedinica u svakom bacanju pada s vjerojatnošću od [tex]1/6[/tex]. Vjerojatnost da jedinica padne točno [tex]i[/tex] puta iznosi [tex]{5 \choose i}(1/6)^i(5/6)^{5-i}[/tex]. Zašto?
Biramo na kojih [tex]i[/tex] kocaka (od ukupno [tex]5[/tex]) će pasti jedinica, to je [tex]{5\choose i}[/tex] događaja, ti događaji su disjunktni a vjerojatnost svakog od njih je [tex](1/6)^i[/tex] (vjerojatnost da na tih [tex]i[/tex] kocaka padne jedinica) puta [tex](5/6)^{5-i}[/tex] (vjerojatnost da na preostalih [tex]5-i[/tex] kocaka ne padne jedinica).
Added after 49 minutes:
Definirajmo potpun sistem događaja: [tex]H_k = [/tex] { u prvom izvlačenju dobili smo sumu [tex]k[/tex] }, za [tex]k=2,3,4[/tex]. [tex]P(H_k)[/tex] je lako izračunati.
Potom analogno definiramo [tex]A_k = [/tex] { u drugom izvlačenju dobili smo sumu [tex]k[/tex] }, za [tex]k=2,3,4[/tex].
Nas zanimaju događaji u kojima je suma jednaka, tj. kad se dogode [tex]H_k[/tex] i [tex]A_k[/tex]. Rješenje je dakle
[tex]P(A_2\cap H_2) + P(A_3\cap H_3) + P(A_4\cap H_4) = P(A_2 | H_2)P(H_2) + P(A_3 | H_3)P(H_3)+P(A_4 | H_4)P(H_4)[/tex],
što ne bi trebalo biti teško izračunati:
- za [tex]P(A_2 | H_2)[/tex] tražimo vjerojatnost da izvučemo dvije manje kovanice ako nam je ostalo 4 manje i 4 veće,
- za [tex]P(A_3 | H_3)[/tex] tražimo vjerojatnost da izvučemo jednu manju i jednu veću kovanicu ako nam je ostalo 5 manjih i 3 veće,
- za [tex]P(A_4 | H_4)[/tex] tražimo vjerojatnost da izvučemo dvije veće kovanice ako nam je ostalo 6 manjih i 2 veće.
|
|
| [Vrh] |
|
akolak
Forumaš(ica)

Pridružen/a: 27. 12. 2010. (16:52:59)
Postovi: (1D)16
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
|
| [Vrh] |
|
zvonkec
Forumaš(ica)

Pridružen/a: 04. 11. 2010. (20:56:30)
Postovi: (37)16
Spol: 
|
|
| [Vrh] |
|
hstojanovic
Forumaš(ica)
Pridružen/a: 16. 10. 2010. (18:00:01)
Postovi: (30)16
Spol: 
|
|
| [Vrh] |
|
matijaB
Forumaš(ica)

Pridružen/a: 19. 08. 2010. (09:11:43)
Postovi: (4D)16
|
|
| [Vrh] |
|
mapat
Forumaš(ica)
Pridružen/a: 01. 11. 2010. (15:31:40)
Postovi: (10)16
Spol: 
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
kobila krsto
Forumaš(ica)
Pridružen/a: 02. 07. 2009. (16:55:08)
Postovi: (6A)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 10:59 čet, 26. 1. 2012 Naslov: Postano: 10:59 čet, 26. 1. 2012 Naslov: |
    |
|
|
2.15
[latex]P( \{a, b\} \cup \{b,c\}) = P( \{a,b,c}\ ) = 1[/latex]
S druge strane:
[latex]P( \{a, b\} \cup \{b,c\}) = P( \{a, b\} ) + P( \{b,c\}) - P( \{a, b\} \cap \{b,c\}) = P( \{a, b\} ) + P( \{b,c\}) - P( \{b\}) [/latex]
Sad odavde izračunaš P(b) i onda možeš lako naći vjerojatnosti od a i c...
2.15
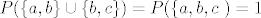
S druge strane:
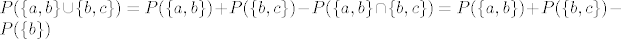
Sad odavde izračunaš P(b) i onda možeš lako naći vjerojatnosti od a i c...
|
|
| [Vrh] |
|
kobila krsto
Forumaš(ica)
Pridružen/a: 02. 07. 2009. (16:55:08)
Postovi: (6A)16
|
|
| [Vrh] |
|
|










