| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 22:41 sub, 7. 1. 2012 Naslov: Postano: 22:41 sub, 7. 1. 2012 Naslov: |
    |
|
|
[quote="N.B."]jel postoji neka dobra dusa koja ce objasniti teorem 17.1 uvjetni ekstremi *-*
[size=9][color=#999999]Added after 36 seconds:[/color][/size]
skripta iz predavanja[/quote]
Znači, ovaj početak ''već smo ranije vidjeli...'' se odnosi na poglavlje Plohe i krivulje II, i tamo je detaljnije objašnjeno, ali mogu ponoviti još jedanput.
Plohu S čine svi oni elementi [latex]\mathbb{R}^n[/latex] za koje vrijedi g(x) = 0. I sad ako imamo neku krivulju na S, nazovimo je c:[latex]\mathbb{R} \rightarrow \mathbb{R}^n[/latex] t.d. je c(0) upravo taj ''naš'' [latex]x_0[/latex] (neka te ova 0 ne zbunjuje, ovo je samo namješteno tako da bude preglednije, da krivulja ''počinje'' upravo od naše točke).
E sad, vrijedi g(c(t)) = 0, za svaki t (zato jer krivulja leži na S, pa svaka njezina točka ispunjava uvjet g(x) = 0) - g(c(t)) je zapravo konstantna funkcija 0 - pa tako vrijedi i da je derivacija od g(c(t)) isto jednaka 0:
[latex]Dg(c(t)) c'(t) = 0[/latex], pa posebno za t = 0 vrijedi:
[latex](grad \hspace{1mm} g(x_0) | c'(0)) = 0[/latex]
Pošto je u [latex]x_0[/latex] lokalni ekstrem funkcije [latex]f|_S[/latex], onda je i derivacija od f(c(t)) u t=0 jednaka nula pa je:
[latex](grad \hspace{1mm} f(x_0) | c'(0)) = 0[/latex]
Eto, mislim da je to dovoljno, ovaj sam finiš je dovoljno dobro objašnjen u skripti, nemam tu više što dodati. :D
| N.B. (napisa): | jel postoji neka dobra dusa koja ce objasniti teorem 17.1 uvjetni ekstremi *-*
Added after 36 seconds:
skripta iz predavanja |
Znači, ovaj početak ''već smo ranije vidjeli...'' se odnosi na poglavlje Plohe i krivulje II, i tamo je detaljnije objašnjeno, ali mogu ponoviti još jedanput.
Plohu S čine svi oni elementi  za koje vrijedi g(x) = 0. I sad ako imamo neku krivulju na S, nazovimo je c: za koje vrijedi g(x) = 0. I sad ako imamo neku krivulju na S, nazovimo je c: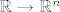 t.d. je c(0) upravo taj ''naš'' t.d. je c(0) upravo taj ''naš''  (neka te ova 0 ne zbunjuje, ovo je samo namješteno tako da bude preglednije, da krivulja ''počinje'' upravo od naše točke). (neka te ova 0 ne zbunjuje, ovo je samo namješteno tako da bude preglednije, da krivulja ''počinje'' upravo od naše točke).
E sad, vrijedi g(c(t)) = 0, za svaki t (zato jer krivulja leži na S, pa svaka njezina točka ispunjava uvjet g(x) = 0) - g(c(t)) je zapravo konstantna funkcija 0 - pa tako vrijedi i da je derivacija od g(c(t)) isto jednaka 0:
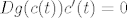 , pa posebno za t = 0 vrijedi: , pa posebno za t = 0 vrijedi:
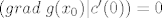
Pošto je u  lokalni ekstrem funkcije lokalni ekstrem funkcije 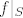 , onda je i derivacija od f(c(t)) u t=0 jednaka nula pa je: , onda je i derivacija od f(c(t)) u t=0 jednaka nula pa je:
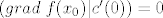
Eto, mislim da je to dovoljno, ovaj sam finiš je dovoljno dobro objašnjen u skripti, nemam tu više što dodati. 
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
 Postano: 9:59 ned, 8. 1. 2012 Naslov: Postano: 9:59 ned, 8. 1. 2012 Naslov: |
    |
|
|
[quote="sz"]Da, dvije ravnine su okomite akko su njihove normale okomite, a normale su tu grad F(x, y, z) i (1, -1, -1).[/quote]
ja tu dobijem na kraju da je ravnina koja bi sadrzavala te tocke Xo+Yo=4 za te tocke Xo, Yo, Zo...jel to dobro,i kakav komentar treba biti uz to?
radi se o drugom zadatku ovdje http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/kolokvij2.pdf
| sz (napisa): | | Da, dvije ravnine su okomite akko su njihove normale okomite, a normale su tu grad F(x, y, z) i (1, -1, -1). |
ja tu dobijem na kraju da je ravnina koja bi sadrzavala te tocke Xo+Yo=4 za te tocke Xo, Yo, Zo...jel to dobro,i kakav komentar treba biti uz to?
radi se o drugom zadatku ovdje http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/kolokvij2.pdf
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
 Postano: 18:10 ned, 8. 1. 2012 Naslov: Postano: 18:10 ned, 8. 1. 2012 Naslov: |
    |
|
|
Ako se ne varam, već je riješen na ovoj temi.
[quote="sz"]
Jednadžba tangencijalne ravnine u [tex](x_0,y_0,z_0)[/tex] mi je ispala
[dtex]\frac{x}{\sqrt[3]{x_0}}+\frac{y}{\sqrt[3]{y_0}}+\frac{z}{\sqrt[3]{z_0}}=a^{\frac{2}{3}}.[/dtex]
Odsječak na osi x je x-koordinata točke ravnine (nešto, 0, 0), ispadne [tex]\sqrt[3]{x_0}a^{\frac{2}{3}}[/tex], analogno za odsječke na y - i z-osi. Kad se svi kvadrati zbroje, opet se iskoristi jednadžba skupa i dobije se [tex]a^2[/tex], što ne ovisi o [tex](x_0,y_0,z_0)[/tex].[/quote]
Ako se ne varam, već je riješen na ovoj temi.
| sz (napisa): |
Jednadžba tangencijalne ravnine u [tex](x_0,y_0,z_0)[/tex] mi je ispala
[dtex]\frac{x}{\sqrt[3]{x_0}}+\frac{y}{\sqrt[3]{y_0}}+\frac{z}{\sqrt[3]{z_0}}=a^{\frac{2}{3}}.[/dtex]
Odsječak na osi x je x-koordinata točke ravnine (nešto, 0, 0), ispadne [tex]\sqrt[3]{x_0}a^{\frac{2}{3}}[/tex], analogno za odsječke na y - i z-osi. Kad se svi kvadrati zbroje, opet se iskoristi jednadžba skupa i dobije se [tex]a^2[/tex], što ne ovisi o [tex](x_0,y_0,z_0)[/tex]. |
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
sz
Forumaš(ica)


Pridružen/a: 26. 01. 2011. (15:17:39)
Postovi: (35)16
|
 Postano: 21:00 ned, 8. 1. 2012 Naslov: Postano: 21:00 ned, 8. 1. 2012 Naslov: |
    |
|
|
[quote="Joker"][quote="sz"]Da, dvije ravnine su okomite akko su njihove normale okomite, a normale su tu grad F(x, y, z) i (1, -1, -1).[/quote]
ja tu dobijem na kraju da je ravnina koja bi sadrzavala te tocke Xo+Yo=4 za te tocke Xo, Yo, Zo...jel to dobro,i kakav komentar treba biti uz to?
radi se o drugom zadatku ovdje http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/kolokvij2.pdf[/quote]
Meni izgleda OK. Od komentara, na početku ukratko objasnimo zašto raspisujemo baš to što raspisujemo (jer je uvjet zadatka ekvivalentan s okomitošću normala na ravnine), i na kraju zaključimo da smo dobili da sve točke koje zadovoljavaju dano svojstvo zadovoljavaju jednadžbu iste ravnine, tj. leže na istoj ravnini, što je i trebalo pokazati. Nema se što previše filozofirati, bitno je da se iz rješenja vidi da je tebi jasno zašto radiš to što radiš.
[size=9][color=#999999]Added after 6 minutes:[/color][/size]
[quote="ceps"]Ima tko hint za 5b ? http://web.math.pmf.unizg.hr/nastava/difraf/dif/2010-11/kolokvij1.pdf[/quote]
Valjda misliš na 6b (5b je dokaz iz predavanja). Mislim da ovdje treba pisati "maksimum" (inače je npr. fja [tex]x^2[/tex] kontraprimjer tvrdnji koju treba dokazati). U tom slučaju tvrdnja slijedi iz činjenice da, kad bi se globalni maksimum postizao u interioru kugle, onda bi u njemu Hesseova matrica bila negativno semidefinitna, što je kontradikcija s pozitivnom definitnošću u svakoj točki.
| Joker (napisa): | | sz (napisa): | | Da, dvije ravnine su okomite akko su njihove normale okomite, a normale su tu grad F(x, y, z) i (1, -1, -1). |
ja tu dobijem na kraju da je ravnina koja bi sadrzavala te tocke Xo+Yo=4 za te tocke Xo, Yo, Zo...jel to dobro,i kakav komentar treba biti uz to?
radi se o drugom zadatku ovdje http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/kolokvij2.pdf |
Meni izgleda OK. Od komentara, na početku ukratko objasnimo zašto raspisujemo baš to što raspisujemo (jer je uvjet zadatka ekvivalentan s okomitošću normala na ravnine), i na kraju zaključimo da smo dobili da sve točke koje zadovoljavaju dano svojstvo zadovoljavaju jednadžbu iste ravnine, tj. leže na istoj ravnini, što je i trebalo pokazati. Nema se što previše filozofirati, bitno je da se iz rješenja vidi da je tebi jasno zašto radiš to što radiš.
Added after 6 minutes:
Valjda misliš na 6b (5b je dokaz iz predavanja). Mislim da ovdje treba pisati "maksimum" (inače je npr. fja [tex]x^2[/tex] kontraprimjer tvrdnji koju treba dokazati). U tom slučaju tvrdnja slijedi iz činjenice da, kad bi se globalni maksimum postizao u interioru kugle, onda bi u njemu Hesseova matrica bila negativno semidefinitna, što je kontradikcija s pozitivnom definitnošću u svakoj točki.
|
|
| [Vrh] |
|
googol
Forumaš(ica)


Pridružen/a: 29. 09. 2011. (21:23:09)
Postovi: (71)16
Spol: 
|
 Postano: 23:42 ned, 8. 1. 2012 Naslov: Postano: 23:42 ned, 8. 1. 2012 Naslov: |
    |
|
|
[quote="sz"][quote="Anonymous"]Moze netko raspisati drugi zadatak u drugom kolokviju iz 2009 http://web.math.pmf.unizg.hr/nastava/difraf/dif/2008-09/kolokvij2.pdf
Vidila sam u nekom topicu ovu uputu :
[quote="Milojko"][quote="Lafel"]
[b]2. zadatak[/b]
Ima netko ideju? Krenuh naime tražiti jednadžbu tangencijalne ravnine, ali nisam daleko dospjela. :?
[/quote]
opći oblik tgc. ravnine u točki (x0,y0,z0), uvrštavaš u nju točke (x,0,0), (y,0,0), (z,0,0) da nađeš presjeke sa koordinatnim osima. negdje se u tome pojavi x0^2/3+y0^2/3+z0^2/3 (il eventualno sve pomnoženo sa minus jedan, ili tako nešto), a pošto je taj (x0,y0,z0) sa plohe, ta suma je jednaka a^2/3. prek toga izraziš x, y, z, i dobiš nešt tipa da je sve kad se kvadrira jednako a, ili tako neka konstanta.
Nisam riješio zad, vidio kod frenda rješenje, ovo je kolko se sjećam, sad ću oprobat.[/quote]
ali mi nešto uporno ispada krivo :([/quote]
Jednadžba tangencijalne ravnine u [tex](x_0,y_0,z_0)[/tex] mi je ispala
[dtex]\frac{x}{\sqrt[3]{x_0}}+\frac{y}{\sqrt[3]{y_0}}+\frac{z}{\sqrt[3]{z_0}}=a^{\frac{2}{3}}.[/dtex]
Odsječak na osi x je x-koordinata točke ravnine (nešto, 0, 0), ispadne [tex]\sqrt[3]{x_0}a^{\frac{2}{3}}[/tex], analogno za odsječke na y - i z-osi. Kad se svi kvadrati zbroje, opet se iskoristi jednadžba skupa i dobije se [tex]a^2[/tex], što ne ovisi o [tex](x_0,y_0,z_0)[/tex].[/quote]
Moze, molim vas, korak po korak rjesenje? Hvala.
| sz (napisa): | | Anonymous (napisa): | Moze netko raspisati drugi zadatak u drugom kolokviju iz 2009 http://web.math.pmf.unizg.hr/nastava/difraf/dif/2008-09/kolokvij2.pdf
Vidila sam u nekom topicu ovu uputu :
| Milojko (napisa): | | Lafel (napisa): |
2. zadatak
Ima netko ideju? Krenuh naime tražiti jednadžbu tangencijalne ravnine, ali nisam daleko dospjela. 
|
opći oblik tgc. ravnine u točki (x0,y0,z0), uvrštavaš u nju točke (x,0,0), (y,0,0), (z,0,0) da nađeš presjeke sa koordinatnim osima. negdje se u tome pojavi x0^2/3+y0^2/3+z0^2/3 (il eventualno sve pomnoženo sa minus jedan, ili tako nešto), a pošto je taj (x0,y0,z0) sa plohe, ta suma je jednaka a^2/3. prek toga izraziš x, y, z, i dobiš nešt tipa da je sve kad se kvadrira jednako a, ili tako neka konstanta.
Nisam riješio zad, vidio kod frenda rješenje, ovo je kolko se sjećam, sad ću oprobat. |
ali mi nešto uporno ispada krivo  |
Jednadžba tangencijalne ravnine u [tex](x_0,y_0,z_0)[/tex] mi je ispala
[dtex]\frac{x}{\sqrt[3]{x_0}}+\frac{y}{\sqrt[3]{y_0}}+\frac{z}{\sqrt[3]{z_0}}=a^{\frac{2}{3}}.[/dtex]
Odsječak na osi x je x-koordinata točke ravnine (nešto, 0, 0), ispadne [tex]\sqrt[3]{x_0}a^{\frac{2}{3}}[/tex], analogno za odsječke na y - i z-osi. Kad se svi kvadrati zbroje, opet se iskoristi jednadžba skupa i dobije se [tex]a^2[/tex], što ne ovisi o [tex](x_0,y_0,z_0)[/tex]. |
Moze, molim vas, korak po korak rjesenje? Hvala.
|
|
| [Vrh] |
|
Kicu
Gost
|
|
| [Vrh] |
|
Kicu
Gost
|
|
| [Vrh] |
|
|






