| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 22:41 ned, 15. 1. 2012 Naslov: Postano: 22:41 ned, 15. 1. 2012 Naslov: |
    |
|
|
[quote="smajl"]Ma imam ja doma onu debelu knjizurinu iz vjerojatnosti, pa sam to malo proucavala i gledala i ovo s neta, pa mi nije bilo jasno sta je tu tocno iskaz teorema, jer nije isto napisano u knjzi kao i na netu :oops: pa reko ajmo provjerit na forumu jer svi znamo kako profesor voli da sve bude precizno iskazano i dokazano :D :D[/quote]
Pa, zapravo i je isto. Na wikiju, onaj prvi iskaz:
Suppose ƒ is a continuous complex-valued function defined on the real interval [a,b]. For every ε > 0, there exists a polynomial function p over C such that for all x in [a,b], we have | ƒ(x) − p(x) | < ε,[b] or equivalently, the supremum norm[/b] || ƒ − p || < ε. If ƒ is real-valued, the polynomial function can be taken over R.
A ova ''supremum norma'' je na zatvorenom intervalu max-norma
http://en.wikipedia.org/wiki/Supremum_norm
pa onaj kraj dokaza u Sarapinoj knjizi:
...odavde slijedi
[latex]lim_n [ max_{0 \leq p \leq 1} |g(p) - B_n(p)| ] = 0 [/latex], što je i tvrdnja teorema.
ima više smisla. :)
Ako slušaš DIFRAF, max-norma ti ne bi trebala biti nešto strano.
Ima i tu još nešto o tome: http://en.wikipedia.org/wiki/Bernstein_polynomial
P.S. Al da, i meni nema baš smisla način na koji je taj teorem prezentiran. Ko prvo, nit ima neke veze sa predmetom, nit je iskazan kako treba. Možda je profesor mislio da smo to radili u osnovnoj. :D
| smajl (napisa): | Ma imam ja doma onu debelu knjizurinu iz vjerojatnosti, pa sam to malo proucavala i gledala i ovo s neta, pa mi nije bilo jasno sta je tu tocno iskaz teorema, jer nije isto napisano u knjzi kao i na netu  pa reko ajmo provjerit na forumu jer svi znamo kako profesor voli da sve bude precizno iskazano i dokazano pa reko ajmo provjerit na forumu jer svi znamo kako profesor voli da sve bude precizno iskazano i dokazano   |
Pa, zapravo i je isto. Na wikiju, onaj prvi iskaz:
Suppose ƒ is a continuous complex-valued function defined on the real interval [a,b]. For every ε > 0, there exists a polynomial function p over C such that for all x in [a,b], we have | ƒ(x) − p(x) | < ε, or equivalently, the supremum norm || ƒ − p || < ε. If ƒ is real-valued, the polynomial function can be taken over R.
A ova ''supremum norma'' je na zatvorenom intervalu max-norma
http://en.wikipedia.org/wiki/Supremum_norm
pa onaj kraj dokaza u Sarapinoj knjizi:
...odavde slijedi
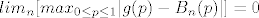 , što je i tvrdnja teorema. , što je i tvrdnja teorema.
ima više smisla. 
Ako slušaš DIFRAF, max-norma ti ne bi trebala biti nešto strano.
Ima i tu još nešto o tome: http://en.wikipedia.org/wiki/Bernstein_polynomial
P.S. Al da, i meni nema baš smisla način na koji je taj teorem prezentiran. Ko prvo, nit ima neke veze sa predmetom, nit je iskazan kako treba. Možda je profesor mislio da smo to radili u osnovnoj. 
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 8:45 pon, 16. 1. 2012 Naslov: Postano: 8:45 pon, 16. 1. 2012 Naslov: |
    |
|
|
Ono što želimo pokazati u tom slučaju je:
[latex]X(\omega) \leq x_n, \forall n \rightarrow X(w) \leq x[/latex]
(koristim iste oznake kao u bilježnici, niz [latex]x_n, n \in \mathbb{N}[/latex] ''pada'' u [latex]x[/latex] - preciznije, [latex]lim_n \ x_n = x, \ x_{n+1} < x_n, \forall n[/latex])
E pa, pretpostavimo suprotno:
[latex]X(\omega) \leq x_n, \ \forall n \ \& \ X(\omega) > x[/latex]
Što se ovdje odmah ne vidi poprilično jasna kontradikcija sa samom definicijom limesa?
Ovako pomalo neformalno, u svakoj okolini, ma koliko maloj, od x se može naći neki [latex]x_n[/latex] - zbog ovih dodatnih svojstava, znamo da se xn-ovi nalaze sa desne strane od x.
Kad bi vrijedilo da je [latex]X(\omega) > x[/latex], zamisli si to na brojevnom pravcu - a uvijek između tog [latex]X(\omega)[/latex] i x-a postoji još mjesta - mjesta u kojem se nalazi još x_n-ova.
A rekli smo da je [latex]X(\omega)[/latex] manji od svakog x_n-a.
Ono što želimo pokazati u tom slučaju je:
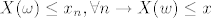
(koristim iste oznake kao u bilježnici, niz 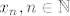 ''pada'' u ''pada'' u  - preciznije, - preciznije, 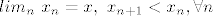 ) )
E pa, pretpostavimo suprotno:
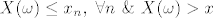
Što se ovdje odmah ne vidi poprilično jasna kontradikcija sa samom definicijom limesa?
Ovako pomalo neformalno, u svakoj okolini, ma koliko maloj, od x se može naći neki 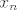 - zbog ovih dodatnih svojstava, znamo da se xn-ovi nalaze sa desne strane od x. - zbog ovih dodatnih svojstava, znamo da se xn-ovi nalaze sa desne strane od x.
Kad bi vrijedilo da je 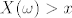 , zamisli si to na brojevnom pravcu - a uvijek između tog , zamisli si to na brojevnom pravcu - a uvijek između tog 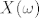 i x-a postoji još mjesta - mjesta u kojem se nalazi još x_n-ova. i x-a postoji još mjesta - mjesta u kojem se nalazi još x_n-ova.
A rekli smo da je 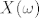 manji od svakog x_n-a. manji od svakog x_n-a.
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 20:17 pon, 16. 1. 2012 Naslov: Postano: 20:17 pon, 16. 1. 2012 Naslov: |
    |
|
|
Ako je očekivanje konačna suma, pravilo trokuta.
Ako je očekivanje red, onda taj red apsolutno konvergira - Teorem 6.5. u skripti prof. Guljaša - http://web.math.pmf.unizg.hr/~guljas/skripte/MATANALuR.pdf (Analiza 2)
Nismo radili u osnovnoj, ali prošle godine jesmo. :)
Većina stvari što je profesor preskočio u objašnjavanju je nešto iz Analize 2. Pogotovo u tom poglavlju o očekivanju, u skoro svakom teoremu koristi ''dobra'' svojstva apsolutno konvergentnih redova, pa nije loše to malo ponoviti.
Ako je očekivanje konačna suma, pravilo trokuta.
Ako je očekivanje red, onda taj red apsolutno konvergira - Teorem 6.5. u skripti prof. Guljaša - http://web.math.pmf.unizg.hr/~guljas/skripte/MATANALuR.pdf (Analiza 2)
Nismo radili u osnovnoj, ali prošle godine jesmo. 
Većina stvari što je profesor preskočio u objašnjavanju je nešto iz Analize 2. Pogotovo u tom poglavlju o očekivanju, u skoro svakom teoremu koristi ''dobra'' svojstva apsolutno konvergentnih redova, pa nije loše to malo ponoviti.
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
Ivanaa
Forumaš(ica)
Pridružen/a: 18. 10. 2010. (22:26:06)
Postovi: (35)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
|
| [Vrh] |
|
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
|
| [Vrh] |
|
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
michelangelo
Forumaš(ica)

Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
|










