| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
kiara
Forumaš(ica)

Pridružen/a: 15. 11. 2011. (23:22:57)
Postovi: (55)16
|
|
| [Vrh] |
|
student_92
Forumaš(ica)

Pridružen/a: 17. 09. 2011. (16:31:46)
Postovi: (B9)16
|
 Postano: 13:17 sri, 11. 4. 2012 Naslov: Postano: 13:17 sri, 11. 4. 2012 Naslov: |
    |
|
|
Evo ja ti mogu pomoći oko 2. zadatka. Ali meni bi dobro došla pomoć[b][i] oko 4. i 5.[/i][/b] :)
Vjerojatno postoji elegantnije rješenje, ali ni ovo nije krivo. Za početak vrlo precizno skiciraj da bi mogla pratiti oznake. Pogledaj trokute ABB1 i CBC1. Oni su slični pa su im odgovarajući kutovi jednaki, tj. BAB1 = C1CB, AB1B = CBC1 i B1BA = BC1C. Kako je četverokut ABCD paralelogram, to vrijedi za kutove DAB = BCD i ABC = CDA. Također slijedi |AB| = a = |CD|, |BC|= b = |AD|.
Sada se lako vidi da su trokuti DAB1 i C1CD sukladni po S-K-S teoremu o sukladnosti.
Tada je |C1D| = |DB1|.
Preostaje još dokazati da su kutovi C1DB1 i BAB1 jednaki. Tu opet ima raspisivanja, a do toga možeš doći ako kreneš od položaja kuta C1DB1 unutar paralelograma. Kada to dokažeš, onda ćeš dobiti da prema K-S-K teoremu o sličnosti slijedi tvrdnja.
Evo ja ti mogu pomoći oko 2. zadatka. Ali meni bi dobro došla pomoć oko 4. i 5. 
Vjerojatno postoji elegantnije rješenje, ali ni ovo nije krivo. Za početak vrlo precizno skiciraj da bi mogla pratiti oznake. Pogledaj trokute ABB1 i CBC1. Oni su slični pa su im odgovarajući kutovi jednaki, tj. BAB1 = C1CB, AB1B = CBC1 i B1BA = BC1C. Kako je četverokut ABCD paralelogram, to vrijedi za kutove DAB = BCD i ABC = CDA. Također slijedi |AB| = a = |CD|, |BC|= b = |AD|.
Sada se lako vidi da su trokuti DAB1 i C1CD sukladni po S-K-S teoremu o sukladnosti.
Tada je |C1D| = |DB1|.
Preostaje još dokazati da su kutovi C1DB1 i BAB1 jednaki. Tu opet ima raspisivanja, a do toga možeš doći ako kreneš od položaja kuta C1DB1 unutar paralelograma. Kada to dokažeš, onda ćeš dobiti da prema K-S-K teoremu o sličnosti slijedi tvrdnja.
|
|
| [Vrh] |
|
matkec
Forumaš(ica)


Pridružen/a: 14. 05. 2010. (16:21:29)
Postovi: (8C)16
|
|
| [Vrh] |
|
kiara
Forumaš(ica)

Pridružen/a: 15. 11. 2011. (23:22:57)
Postovi: (55)16
|
|
| [Vrh] |
|
matkec
Forumaš(ica)


Pridružen/a: 14. 05. 2010. (16:21:29)
Postovi: (8C)16
|
 Postano: 17:23 pon, 16. 4. 2012 Naslov: Postano: 17:23 pon, 16. 4. 2012 Naslov: |
    |
|
|
Nema problema.
Strategija ti je da kreneš od tog kuta, raspisuješ kojima je taj kut jednak i "približavaš" se točki N.
(Također, ako se na jednom dijelu zbuniš, i vidiš da ja spominjem nekih 180 stupnjeva koji će ti se činiti čudnima, to je zbog toga što vjerovatno imamo drugačije skice. Kod mene N leži na stranici CD, a točka M na produžetku pravca CB preko točke B.)
Dakle:
MSB
=MAB (zbog tetivnog MBSA, tetiva MB)
=MAS-BAS
=(180-MBS)-BAC (tetivni MBSA, zbroj nasuprotnih je 180)
=CBS-BAC
=CBD-BAC=
=CAD-BDC (tetivni ABCD, tetive CD i BC)
Nismo došli skroz do točke N, ali ako kreneš sad od kuta NSD sa sličan način kao ovdje, doći ćeš do iste zadnje linije.
Tako ćeš pokazati da je kut MSB = kut NSD. Razlog zašto ti se to "sviđa" je sljedeći:
Ti znaš da su točke B, S, D kolinearne. Zato ako vrijedi ova jednakost gore, tada će i točke M, S, N biti kolinearne. Formalno:
B, S, D kolinearne => kut BSD=180 => kut DSN + kut NSB = 180 => kut DSN + kut NSM - kut BSM = 180 => kut NSM = 180 => N, S, M kolinearne
Nema problema.
Strategija ti je da kreneš od tog kuta, raspisuješ kojima je taj kut jednak i "približavaš" se točki N.
(Također, ako se na jednom dijelu zbuniš, i vidiš da ja spominjem nekih 180 stupnjeva koji će ti se činiti čudnima, to je zbog toga što vjerovatno imamo drugačije skice. Kod mene N leži na stranici CD, a točka M na produžetku pravca CB preko točke B.)
Dakle:
MSB
=MAB (zbog tetivnog MBSA, tetiva MB)
=MAS-BAS
=(180-MBS)-BAC (tetivni MBSA, zbroj nasuprotnih je 180)
=CBS-BAC
=CBD-BAC=
=CAD-BDC (tetivni ABCD, tetive CD i BC)
Nismo došli skroz do točke N, ali ako kreneš sad od kuta NSD sa sličan način kao ovdje, doći ćeš do iste zadnje linije.
Tako ćeš pokazati da je kut MSB = kut NSD. Razlog zašto ti se to "sviđa" je sljedeći:
Ti znaš da su točke B, S, D kolinearne. Zato ako vrijedi ova jednakost gore, tada će i točke M, S, N biti kolinearne. Formalno:
B, S, D kolinearne => kut BSD=180 => kut DSN + kut NSB = 180 => kut DSN + kut NSM - kut BSM = 180 => kut NSM = 180 => N, S, M kolinearne
|
|
| [Vrh] |
|
boksi
Forumaš(ica)

Pridružen/a: 02. 09. 2011. (16:37:55)
Postovi: (44)16
Spol: 
|
 Postano: 21:26 uto, 17. 4. 2012 Naslov: Postano: 21:26 uto, 17. 4. 2012 Naslov: |
    |
|
|
ako nije problem, može li mi 5.zadatak ipak malo pobliže objasniti netko. ne uspijevam ni započeti pošteno unatoč hintu.
i, da, matkec, u hintu za treći zadatak, kut AOB = 90, ne 45 :)
ako nije problem, može li mi 5.zadatak ipak malo pobliže objasniti netko. ne uspijevam ni započeti pošteno unatoč hintu.
i, da, matkec, u hintu za treći zadatak, kut AOB = 90, ne 45 
|
|
| [Vrh] |
|
gflegar
Forumaš(ica)


Pridružen/a: 12. 10. 2011. (15:03:41)
Postovi: (10D)16
Spol: 
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
 Postano: 2:59 sri, 18. 4. 2012 Naslov: Postano: 2:59 sri, 18. 4. 2012 Naslov: |
    |
|
|
[quote="matkec"]Hint za 3. zadatak:
Spusti ortogonalne projekcije iz P na pravce OA i OB, pa gledaj pravokutne trokute koje dobiješ. Ne zaboravi da je [latex]\angle AOB =45^o[/latex].
[/quote]
Gledam hint, gledam pravokutne trokute i ne vidim ništa xD
Dobijam stalno [tex]|PC|^2+|PD|^2=|AB|^2+x, \ x>0[/tex], a x mi je tu neki žnj broj.
Može li mi, molim vas, netko raspisati prvi korak, dva, samo da vidim u kojem smjeru moram ići.
Unaprijed hvala! :thankyou:
| matkec (napisa): | Hint za 3. zadatak:
Spusti ortogonalne projekcije iz P na pravce OA i OB, pa gledaj pravokutne trokute koje dobiješ. Ne zaboravi da je 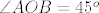 . .
|
Gledam hint, gledam pravokutne trokute i ne vidim ništa xD
Dobijam stalno [tex]|PC|^2+|PD|^2=|AB|^2+x, \ x>0[/tex], a x mi je tu neki žnj broj.
Može li mi, molim vas, netko raspisati prvi korak, dva, samo da vidim u kojem smjeru moram ići.
Unaprijed hvala! 
|
|
| [Vrh] |
|
gflegar
Forumaš(ica)


Pridružen/a: 12. 10. 2011. (15:03:41)
Postovi: (10D)16
Spol: 
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
|
| [Vrh] |
|
5_ra
Forumaš(ica)

Pridružen/a: 10. 12. 2011. (15:37:14)
Postovi: (28)16
|
|
| [Vrh] |
|
aj_ca_volin_te
Forumaš(ica)


Pridružen/a: 22. 11. 2011. (20:18:49)
Postovi: (6F)16
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
|
| [Vrh] |
|
matkec
Forumaš(ica)


Pridružen/a: 14. 05. 2010. (16:21:29)
Postovi: (8C)16
|
|
| [Vrh] |
|
|







