| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
 Postano: 10:37 uto, 17. 4. 2012 Naslov: Re: teorijsko pitanje Postano: 10:37 uto, 17. 4. 2012 Naslov: Re: teorijsko pitanje |
    |
|
|
[quote="satja"]Imamo dvije konačne grupe s istim brojem članova. Za svaki član iz obje grupe izračunamo njegov red. Ako se redovi iz prve grupe podudaraju s redovima iz druge grupe, jesu li grupe nužno izomorfne?[/quote]
Ako se ne varam, onda ukoliko su to dvije konačne Abelove grupe, onda zbog strukturnog teorema o konačno generiranim Abelovim grupama tvrdnja vrijedi.
Inače, ne!
Nisam se sam domislio primjeru, pa ću staviti [url=http://mathoverflow.net/questions/31249/order-information-enough-to-guarantee-1-isomorphism]referencu[/url] :)
Uglavnom ako sa [latex]Q=\{1,\pm i, \pm j, \pm k\}[/latex] označimo grupu kvaterniona onda [latex]Q\times\mathbb{Z}_2[/latex] i grupa [latex]\mathbb{Z}_4\times\mathbb{Z}_4[/latex] imaju istu statistiku redova elemenata iako nisu izomorfne (jedna je Abelova, a druga nije).
Preduhitren sam :'(
| satja (napisa): | | Imamo dvije konačne grupe s istim brojem članova. Za svaki član iz obje grupe izračunamo njegov red. Ako se redovi iz prve grupe podudaraju s redovima iz druge grupe, jesu li grupe nužno izomorfne? |
Ako se ne varam, onda ukoliko su to dvije konačne Abelove grupe, onda zbog strukturnog teorema o konačno generiranim Abelovim grupama tvrdnja vrijedi.
Inače, ne!
Nisam se sam domislio primjeru, pa ću staviti referencu 
Uglavnom ako sa 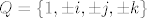 označimo grupu kvaterniona onda označimo grupu kvaterniona onda 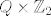 i grupa i grupa 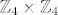 imaju istu statistiku redova elemenata iako nisu izomorfne (jedna je Abelova, a druga nije). imaju istu statistiku redova elemenata iako nisu izomorfne (jedna je Abelova, a druga nije).
Preduhitren sam :'(
_________________
Jedan je smjer očit, a drugi je trivijalan.
|
|
| [Vrh] |
|
|





