| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
kalasnikov44
Forumaš(ica)

Pridružen/a: 29. 02. 2012. (19:52:58)
Postovi: (2)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 21:44 pon, 23. 4. 2012 Naslov: Postano: 21:44 pon, 23. 4. 2012 Naslov: |
    |
|
|
Koristis formule koje znas. Na primjer, prvi:
Imas: [tex]\alpha - \beta = 25^\circ[/tex]
Znas: [tex]\alpha + \beta + \gamma = 180^\circ, \quad \gamma = 90^\circ \quad \Rightarrow \quad \alpha + \beta = 180^\circ - \gamma = 90^\circ[/tex]
Rijesis sustav dvije jednadzbe s dvije nepoznanice i dobijes:
[tex]\alpha = \frac{90^\circ + 25^\circ}{2}, \quad \beta = \frac{90^\circ - 25^\circ}{2}[/tex]
Sada znas kuteve, a znas i da je
[tex]\sin \alpha = \cos \beta = \frac{a}{c}, \quad \sin \beta = \cos \alpha = \frac{b}{c}[/tex].
Odatle zakljucis, na primjer,
[tex]a = c \sin \alpha, \quad b = c \sin \beta[/tex], (*)
a u zadatku imas zadano:
[tex]a + b = 31[/tex]
Zajedno, to ti daje:
[tex]31 = a + b = c \sin \alpha + c \sin \beta = c (\sin \alpha + c \sin \beta)[/tex].
Kuteve znas, pa dobijes hipotenuzu [tex]c[/tex].
Slicno, u drugom imas da je:
[tex]\frac{a}{c} = \frac{2}{5}, \quad 90.4 = P = \frac{ab}{2} = \frac{a\sqrt{c^2-a^2}}{2}[/tex].
Iz prve dobijes da je [tex]a = \frac{2c}{5}[/tex], uvrstis u drugu i dobijes hipotenuzu [tex]c[/tex]. Kuteve izvadis preko (*) od gore, a onda imas i katete.
Treci skiciraj i vidjet ces da imas dva pravokutna trokuta.
A sad malo sam probavaj, pa kad zapnes napisi sto si radio i gdje je zapelo.
Koristis formule koje znas. Na primjer, prvi:
Imas: [tex]\alpha - \beta = 25^\circ[/tex]
Znas: [tex]\alpha + \beta + \gamma = 180^\circ, \quad \gamma = 90^\circ \quad \Rightarrow \quad \alpha + \beta = 180^\circ - \gamma = 90^\circ[/tex]
Rijesis sustav dvije jednadzbe s dvije nepoznanice i dobijes:
[tex]\alpha = \frac{90^\circ + 25^\circ}{2}, \quad \beta = \frac{90^\circ - 25^\circ}{2}[/tex]
Sada znas kuteve, a znas i da je
[tex]\sin \alpha = \cos \beta = \frac{a}{c}, \quad \sin \beta = \cos \alpha = \frac{b}{c}[/tex].
Odatle zakljucis, na primjer,
[tex]a = c \sin \alpha, \quad b = c \sin \beta[/tex], (*)
a u zadatku imas zadano:
[tex]a + b = 31[/tex]
Zajedno, to ti daje:
[tex]31 = a + b = c \sin \alpha + c \sin \beta = c (\sin \alpha + c \sin \beta)[/tex].
Kuteve znas, pa dobijes hipotenuzu [tex]c[/tex].
Slicno, u drugom imas da je:
[tex]\frac{a}{c} = \frac{2}{5}, \quad 90.4 = P = \frac{ab}{2} = \frac{a\sqrt{c^2-a^2}}{2}[/tex].
Iz prve dobijes da je [tex]a = \frac{2c}{5}[/tex], uvrstis u drugu i dobijes hipotenuzu [tex]c[/tex]. Kuteve izvadis preko (*) od gore, a onda imas i katete.
Treci skiciraj i vidjet ces da imas dva pravokutna trokuta.
A sad malo sam probavaj, pa kad zapnes napisi sto si radio i gdje je zapelo.
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
Neno
Forumaš(ica)

Pridružen/a: 08. 02. 2008. (20:03:15)
Postovi: (98)16
Spol: 
Lokacija: Zagreb
|
 Postano: 8:53 uto, 24. 4. 2012 Naslov: Re: Zadaci iz trigonometrije Postano: 8:53 uto, 24. 4. 2012 Naslov: Re: Zadaci iz trigonometrije |
    |
|
|
[quote="kalasnikov44"]... kako se to riješava...
http://a7.sphotos.ak.fbcdn.net/hphotos-ak-ash3/525239_3156392701684_1021218175_32348696_735802508_n.jpg[/quote]
to se r[b]je[/b]šava, naprimjer 5. zadatak:
[latex]\\P=64\ cm^2\\\alpha=48^\circ20'\\a=?\\e,f=?[/latex]
...............................................................................
[latex]\\\alpha=48^\circ20'\implies \frac{\alpha}{2}=24^\circ10'\\24^\circ10'+90^\circ+\frac{\beta}{2}=180^\circ\implies \frac{\beta}{2}=65^\circ50'\\P_{romba}=a\cdot v\quad (*1)\\\sin\frac{\alpha}{2}=\frac{\frac{e}{2}}{a}=\frac{e}{2a}\quad (*2)\\\sin\alpha=\frac{v}{a}\implies v=a\cdot\sin\alpha\quad (*3)\\[/latex]
[latex]v[/latex] uvrstim u (*1)
[latex]P=a\cdot a\cdot\sin\alpha=a^2\cdot\sin\alpha\implies a^2=\frac{P}{\sin\alpha}=\frac{64}{\sin 48^\circ20'}=85,67\implies\boxed{a=9,26\ cm}\\[/latex]
[latex]a[/latex] uvrstim u (*3)
[latex]v=9,26\cdot\sin 48^\circ20'=6,92\ cm[/latex]
[latex]a[/latex] uvrstim u (*2)
[latex]\boxed{e=\sin 24^\circ10'\cdot 2\cdot 9,26=7,58\ cm}[/latex]
računam još dijagonalu [latex]f[/latex]
[latex]tg\frac{\alpha}{2}=\frac{\frac{e}{2}}{\frac{f}{2}}=\frac{e}{f}\implies\boxed{f=\frac{e}{tg\frac{\alpha}{2}}=\frac{7,58}{0,44}=16,89\ cm}[/latex]
to se rješava, naprimjer 5. zadatak:
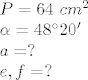
...............................................................................
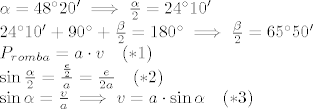
 uvrstim u (*1) uvrstim u (*1)
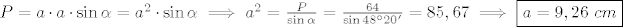
 uvrstim u (*3) uvrstim u (*3)
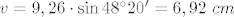
 uvrstim u (*2) uvrstim u (*2)
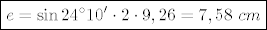
računam još dijagonalu 
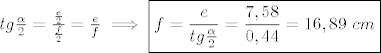
|
|
| [Vrh] |
|
Neno
Forumaš(ica)

Pridružen/a: 08. 02. 2008. (20:03:15)
Postovi: (98)16
Spol: 
Lokacija: Zagreb
|
 Postano: 10:16 uto, 24. 4. 2012 Naslov: Re: Zadaci iz trigonometrije Postano: 10:16 uto, 24. 4. 2012 Naslov: Re: Zadaci iz trigonometrije |
    |
|
|
[quote="kalasnikov44"]kako se to riješava[/quote]
r[b]je[/b]šava se naprimjer 6.
[latex]a=23\ cm\\c=11\ cm\\\alpha=52^\circ10'[/latex]
-------------------------------------------------------
u jednakokračnom trapezu, (23-11):2=6 cm je udaljenost od točke C' do točke B.
[latex]P_{trapeza}=\frac{a+c}{2}\cdot v\\\sin 52^\circ10'=\frac{v}{b}\quad (*1)\\tg 52^\circ10'=\frac{v}{6}\implies v=6\cdot tg 52^\circ10'=7,73\ cm[/latex]
uvrstim [latex]v[/latex] u (*1), jer me pita za krak:
[latex]\boxed{b=\frac{v}{\sin 52^\circ10'}=\frac{7,73}{0,789}=9,79\ cm}[/latex]
i pita me za površinu:
[latex]\boxed{P=\frac{23+11}{2}\cdot 7,73=131,41\ cm^2}[/latex]
| kalasnikov44 (napisa): | | kako se to riješava |
rješava se naprimjer 6.
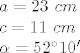
-------------------------------------------------------
u jednakokračnom trapezu, (23-11):2=6 cm je udaljenost od točke C' do točke B.
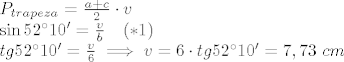
uvrstim  u (*1), jer me pita za krak: u (*1), jer me pita za krak:
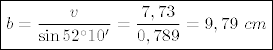
i pita me za površinu:
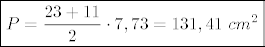
|
|
| [Vrh] |
|
Neno
Forumaš(ica)

Pridružen/a: 08. 02. 2008. (20:03:15)
Postovi: (98)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
bernhard
Forumaš(ica)

Pridružen/a: 23. 03. 2010. (20:38:33)
Postovi: (6E)16
Lokacija: Multiple users - od 2012 profil iskljucivo koristi Maria Culjak
|
|
| [Vrh] |
|
Neno
Forumaš(ica)

Pridružen/a: 08. 02. 2008. (20:03:15)
Postovi: (98)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
kalasnikov44
Forumaš(ica)

Pridružen/a: 29. 02. 2012. (19:52:58)
Postovi: (2)16
|
|
| [Vrh] |
|
|









