Search
 
 
  Engleski
 
 
 
Open in this window (click to change)
Forum@DeGiorgi: Početna
Forum za podršku nastavi na PMF-MO
Login Registracija FAQ Smajlići Članstvo Pretražnik Forum@DeGiorgi: Početna

Redovi
WWW:
Idite na Prethodno  1, 2, 3, 4, 5, 6, 7  Sljedeće
Moja sarma
 
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Matematička analiza 1 i 2
Prethodna tema :: Sljedeća tema  
Autor/ica Poruka
Zenon
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
PostPostano: 17:49 sub, 2. 6. 2012    Naslov: Citirajte i odgovorite
EDIT: NVM, kolega gflegar mi je ljubazno objasnio :D
EDIT: NVM, kolega gflegar mi je ljubazno objasnio Very Happy



_________________
It's a wonderful, wonderful life!
[tex]\heartsuit \ \mathcal{PMF-MO} \ \heartsuit[/tex]
[tex]\mathbb Z\Sigma\mathbb N\emptyset\mathbb N[/tex]

Zadnja promjena: Zenon; 20:12 sub, 2. 6. 2012; ukupno mijenjano 1 put.
[Vrh]
Korisnički profil Pošaljite privatnu poruku
aj_ca_volin_te
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 22. 11. 2011. (20:18:49)
Postovi: (6F)16
Sarma = la pohva - posuda
20 = 22 - 2
PostPostano: 18:57 sub, 2. 6. 2012    Naslov: Citirajte i odgovorite
http://web.math.pmf.unizg.hr/nastava/analiza/kol/ma2-0708-kol2.pdf

moze netko grupa C, 4. zadatak, pod a) HVALA :P
http://web.math.pmf.unizg.hr/nastava/analiza/kol/ma2-0708-kol2.pdf

moze netko grupa C, 4. zadatak, pod a) HVALA Razz


[Vrh]
Korisnički profil Pošaljite privatnu poruku
anamarie
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 07. 09. 2011. (10:59:19)
Postovi: (87)16
Spol: žensko
Sarma = la pohva - posuda
5 = 13 - 8
PostPostano: 19:11 sub, 2. 6. 2012    Naslov: Citirajte i odgovorite
[quote="aj_ca_volin_te"]http://web.math.pmf.unizg.hr/nastava/analiza/kol/ma2-0708-kol2.pdf

moze netko grupa C, 4. zadatak, pod a) HVALA :P[/quote]
[tex] ln\frac{7-x}{(x+1)(7-x)}=-ln(x+1)
[/tex]

uvedeš supstituciju y=x-c=x-3,x=y+3 pa imaš

[tex] -ln(y+4)=-ln(4(\frac{y}{4}+1))=-ln4-ln(\frac{y}{4}+1)
[/tex]

ovo dalje znaš..
aj_ca_volin_te (napisa):
http://web.math.pmf.unizg.hr/nastava/analiza/kol/ma2-0708-kol2.pdf

moze netko grupa C, 4. zadatak, pod a) HVALA Razz

[tex] ln\frac{7-x}{(x+1)(7-x)}=-ln(x+1)
[/tex]

uvedeš supstituciju y=x-c=x-3,x=y+3 pa imaš

[tex] -ln(y+4)=-ln(4(\frac{y}{4}+1))=-ln4-ln(\frac{y}{4}+1)
[/tex]

ovo dalje znaš..


[Vrh]
Korisnički profil Pošaljite privatnu poruku
aj_ca_volin_te
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 22. 11. 2011. (20:18:49)
Postovi: (6F)16
Sarma = la pohva - posuda
20 = 22 - 2
PostPostano: 19:39 sub, 2. 6. 2012    Naslov: Citirajte i odgovorite
ajmeee mene budale, krivo sam izluciva i dobivao nesto gdje je presjek intervala bio prazan :? hvala svejedno :wink:

[size=9][color=#999999]Added after 2 minutes:[/color][/size]

jt nisam pokratia ovo sto je trebalo 8)
ajmeee mene budale, krivo sam izluciva i dobivao nesto gdje je presjek intervala bio prazan Confused hvala svejedno Wink

Added after 2 minutes:

jt nisam pokratia ovo sto je trebalo Cool


[Vrh]
Korisnički profil Pošaljite privatnu poruku
PermutiranoPrase
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 10. 09. 2011. (16:08:19)
Postovi: (F4)16
Spol: kućni ljubimac
Sarma = la pohva - posuda
10 = 17 - 7
PostPostano: 20:21 sub, 2. 6. 2012    Naslov: Citirajte i odgovorite
Nitko nema ideje za moje Taylore? O Svemoćni Zenone? :rose:

[size=18][tex]f(x) = \frac {arcsin x} {\sqrt{1-x^2}}[/tex][/size]

i novi:
[size=18][tex]f(x) = (\frac {x} {x+3})^2[/tex][/size] (iz kolokvija 2009.)
[size=18][tex]f(x) = (\frac {x} {x^2+1})^3[/tex][/size]
Nitko nema ideje za moje Taylore? O Svemoćni Zenone? Imam nesto za tebe

[tex]f(x) = \frac {arcsin x} {\sqrt{1-x^2}}[/tex]

i novi:
[tex]f(x) = (\frac {x} {x+3})^2[/tex] (iz kolokvija 2009.)
[tex]f(x) = (\frac {x} {x^2+1})^3[/tex]



_________________
With great power comes great electricity bill.
n!!!!
Theorem 2: Alexander the Great did not exist and he had an infinite number of limbs.
[Vrh]
Korisnički profil Pošaljite privatnu poruku
student_92
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 17. 09. 2011. (16:31:46)
Postovi: (B9)16
Sarma = la pohva - posuda
10 = 16 - 6
PostPostano: 21:33 sub, 2. 6. 2012    Naslov: Citirajte i odgovorite
[quote="PermutiranoPrase"]Nitko nema ideje za moje Taylore? O Svemoćni Zenone? :rose:[/quote]

Evo nije Zenon, ali eto ;)
Evo ideja: Za onaj s arcsin još nemam ideju :) (tj. nisam ga ni počeo).
Što se drugoga tiče, potenciraj brojnik i nazivnik pa ti se u nazivniku javi (x+3)^2, a tada ti preostaje analizirati samo[tex]\frac {1} {(x+3)^2}[/tex]. Sada možeš uvesti supstituciju t = x/3 tako da ti se pojavi (t+1)^2 pa je to onda pogodno za npr. formulu koja koristi binomni red ili možeš zaključiti čija je to derivacija pa ići na deriviranje član po član.

Treći - pogledaj zadatak 3.23 pod f) u skripti, vrlo je instruktivan.
P.S. Valjda je ovo dobro. Neka netko ispravi ako nije.
PermutiranoPrase (napisa):
Nitko nema ideje za moje Taylore? O Svemoćni Zenone? Imam nesto za tebe


Evo nije Zenon, ali eto Wink
Evo ideja: Za onaj s arcsin još nemam ideju Smile (tj. nisam ga ni počeo).
Što se drugoga tiče, potenciraj brojnik i nazivnik pa ti se u nazivniku javi (x+3)^2, a tada ti preostaje analizirati samo[tex]\frac {1} {(x+3)^2}[/tex]. Sada možeš uvesti supstituciju t = x/3 tako da ti se pojavi (t+1)^2 pa je to onda pogodno za npr. formulu koja koristi binomni red ili možeš zaključiti čija je to derivacija pa ići na deriviranje član po član.

Treći - pogledaj zadatak 3.23 pod f) u skripti, vrlo je instruktivan.
P.S. Valjda je ovo dobro. Neka netko ispravi ako nije.




Zadnja promjena: student_92; 22:11 sub, 2. 6. 2012; ukupno mijenjano 1 put.
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Zenon
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
PostPostano: 21:33 sub, 2. 6. 2012    Naslov: Citirajte i odgovorite
A ne znam još, nisam toliko daleko stigao s vježbanjem :P
Prvi sam integrirao ali ne znam što ću s [tex]\arctan ^2 x[/tex]. Drugi sam relativno uspio, ali dobijem nešto tipa 1+red+2. red što nije dobro.
A treći još gore :lol:
Ako uspijem s vremenom, javim ti :)
A ne znam još, nisam toliko daleko stigao s vježbanjem Razz
Prvi sam integrirao ali ne znam što ću s [tex]\arctan ^2 x[/tex]. Drugi sam relativno uspio, ali dobijem nešto tipa 1+red+2. red što nije dobro.
A treći još gore Laughing
Ako uspijem s vremenom, javim ti Smile



_________________
It's a wonderful, wonderful life!
[tex]\heartsuit \ \mathcal{PMF-MO} \ \heartsuit[/tex]
[tex]\mathbb Z\Sigma\mathbb N\emptyset\mathbb N[/tex]
[Vrh]
Korisnički profil Pošaljite privatnu poruku
quark
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: muško
Sarma = la pohva - posuda
20 = 26 - 6
PostPostano: 22:45 sub, 2. 6. 2012    Naslov: Citirajte i odgovorite
3.30. Odredite radijus konvergencije i interval konvergencije:

[latex]\sum2^{n^{2}} x^{n!}[/latex]

Potpuno sam :shock: , hvala unaprijed :)
3.30. Odredite radijus konvergencije i interval konvergencije:



Potpuno sam Shocked , hvala unaprijed Smile


[Vrh]
Korisnički profil Pošaljite privatnu poruku
gflegar
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 12. 10. 2011. (15:03:41)
Postovi: (10D)16
Spol: muško
Sarma = la pohva - posuda
68 = 72 - 4
PostPostano: 22:47 sub, 2. 6. 2012    Naslov: Citirajte i odgovorite
Evo drugi (mozda ima koja greska :) ):

\begin{align} f(x) &= \frac{x^2}{(x+3)^2} = 1 - 3 \frac{2x + 3}{(x+3)^2} = 1 - 3 \left(\frac{2}{x+3} + \frac{-3}{(x+3)^2} \right) = 1 - 3 \left(\frac{2}{3} \frac{1}{\frac{x}{3}+1} + 3 \frac{-1}{(x + 3)^2} \right) = \\
&= 1 - 3 \left(\frac{2}{3} \frac{1}{\frac{x}{3}+1} + 3 \frac{d}{dx}\left( \frac{1}{3} \frac{1}{\frac{x}{3} + 1}\right) \right)= 1 - 2 \frac{1}{\frac{x}{3}+1} - 3 \frac{d}{dx}\left(\frac{1}{\frac{x}{3} + 1}\right) = \begin{bmatrix} t = -\frac{x}{3} \end{bmatrix} = \\
&= 1 - 2 \frac{1}{1 - t} - 3 \frac{d}{dx}\left(\frac{1}{1 - t}\right) = 1 - 2 \sum_{n = 0}^{\infty} t^n - 3 \frac{d}{dx}\left(1 + \sum_{n = 1}^{\infty} t^n\right) = \\
&= 1 - 2 \sum_{n = 0}^{\infty} (-1)^n\frac{1}{3^n}x^n - 3 \frac{d}{dx}\left(1 + \sum_{n = 1}^{\infty} (-1)^n\frac{1}{3^n}x^n \right) = 1 - 2 \sum_{n = 0}^{\infty} (-1)^n\frac{1}{3^n}x^n +\sum_{n = 1}^{\infty} (-1)^{n-1}\frac{(n - 1) + 1}{3^{n-1}}x^{n - 1} = \\
&= 1 + \sum_{n = 0}^{\infty} (-1)^n\frac{-2}{3^n}x^n +\sum_{n = 0}^{\infty} (-1)^n\frac{n + 1}{3^n}x^n = 1 + \sum_{n = 0}^{\infty} (-1)^n\frac{n - 1}{3^n}x^n = \\
&= \sum_{n = 1}^{\infty} (-1)^n\frac{n - 1}{3^n}x^n\end{align}
Evo drugi (mozda ima koja greska Smile ):

\begin{align} f(x) &= \frac{x^2}{(x+3)^2} = 1 - 3 \frac{2x + 3}{(x+3)^2} = 1 - 3 \left(\frac{2}{x+3} + \frac{-3}{(x+3)^2} \right) = 1 - 3 \left(\frac{2}{3} \frac{1}{\frac{x}{3}+1} + 3 \frac{-1}{(x + 3)^2} \right) = \\
&= 1 - 3 \left(\frac{2}{3} \frac{1}{\frac{x}{3}+1} + 3 \frac{d}{dx}\left( \frac{1}{3} \frac{1}{\frac{x}{3} + 1}\right) \right)= 1 - 2 \frac{1}{\frac{x}{3}+1} - 3 \frac{d}{dx}\left(\frac{1}{\frac{x}{3} + 1}\right) = \begin{bmatrix} t = -\frac{x}{3} \end{bmatrix} = \\
&= 1 - 2 \frac{1}{1 - t} - 3 \frac{d}{dx}\left(\frac{1}{1 - t}\right) = 1 - 2 \sum_{n = 0}^{\infty} t^n - 3 \frac{d}{dx}\left(1 + \sum_{n = 1}^{\infty} t^n\right) = \\
&= 1 - 2 \sum_{n = 0}^{\infty} (-1)^n\frac{1}{3^n}x^n - 3 \frac{d}{dx}\left(1 + \sum_{n = 1}^{\infty} (-1)^n\frac{1}{3^n}x^n \right) = 1 - 2 \sum_{n = 0}^{\infty} (-1)^n\frac{1}{3^n}x^n +\sum_{n = 1}^{\infty} (-1)^{n-1}\frac{(n - 1) + 1}{3^{n-1}}x^{n - 1} = \\
&= 1 + \sum_{n = 0}^{\infty} (-1)^n\frac{-2}{3^n}x^n +\sum_{n = 0}^{\infty} (-1)^n\frac{n + 1}{3^n}x^n = 1 + \sum_{n = 0}^{\infty} (-1)^n\frac{n - 1}{3^n}x^n = \\
&= \sum_{n = 1}^{\infty} (-1)^n\frac{n - 1}{3^n}x^n\end{align}
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail Posjetite Web stranice
Hubert Cumberdale
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 10. 11. 2011. (11:43:04)
Postovi: (24)16
Spol: žensko
Sarma = la pohva - posuda
2 = 3 - 1
PostPostano: 22:57 sub, 2. 6. 2012    Naslov: Citirajte i odgovorite
[quote="Zenon"]Pretpostavljam da te muči apsolutna konvergencija s obzirom da je obična trivijalna.
[tex]e^{-H_n}=\frac{1}{e^{H_n}}[/tex] i sada to usporediš s [tex]\frac 1n[/tex]
[dtex]\frac{\frac{1}{e^{H_n}}}{\frac 1n}=\frac{n}{e^{H_n}}=\frac{1}{e^{H_n}\cdot n^{-1}}=\frac{1}{e^{H_n}\cdot e^{-\ln n}}=\frac{1}{e^{H_n-\ln n}}[/dtex]
i tu imaš Euler-Mascheronijevu konstantu.
[/quote]

Imam pitanje u vezi ovog reda ([tex] \Sigma (-1)^n e^{-H_n})[/tex], tj njegove apsolutne konvergencije... Vjerujem da nešto krivo radim, ali ne mogu shvatiti što. Preko d'Alembertovog kriterija dobivam:

[dtex] \frac{|a_{n+1}|}{|a_{n}|} = \frac{e^{-H_{n+1}}}{e^{-H_n}} = \frac{e^{-(H_{n}+\frac{1}{n+1})}}{e^{-H_n}}=\frac{{e^{-H_n}}*e^{-\frac{1}{n+1}}}{e^{-H_n}} = e^{-\frac{1}{n+1}} < 1 ,[/dtex] iz čega slijedi da je [tex]\Sigma a_n [/tex] apsolutno konvergentan red??

:(

Hvala na pomoći i žao mi je ako sam jako glupa :(
Zenon (napisa):
Pretpostavljam da te muči apsolutna konvergencija s obzirom da je obična trivijalna.
[tex]e^{-H_n}=\frac{1}{e^{H_n}}[/tex] i sada to usporediš s [tex]\frac 1n[/tex]
[dtex]\frac{\frac{1}{e^{H_n}}}{\frac 1n}=\frac{n}{e^{H_n}}=\frac{1}{e^{H_n}\cdot n^{-1}}=\frac{1}{e^{H_n}\cdot e^{-\ln n}}=\frac{1}{e^{H_n-\ln n}}[/dtex]
i tu imaš Euler-Mascheronijevu konstantu.


Imam pitanje u vezi ovog reda ([tex] \Sigma (-1)^n e^{-H_n})[/tex], tj njegove apsolutne konvergencije... Vjerujem da nešto krivo radim, ali ne mogu shvatiti što. Preko d'Alembertovog kriterija dobivam:

[dtex] \frac{|a_{n+1}|}{|a_{n}|} = \frac{e^{-H_{n+1}}}{e^{-H_n}} = \frac{e^{-(H_{n}+\frac{1}{n+1})}}{e^{-H_n}}=\frac{{e^{-H_n}}*e^{-\frac{1}{n+1}}}{e^{-H_n}} = e^{-\frac{1}{n+1}} < 1 ,[/dtex] iz čega slijedi da je [tex]\Sigma a_n [/tex] apsolutno konvergentan red??

Sad

Hvala na pomoći i žao mi je ako sam jako glupa Sad


[Vrh]
Korisnički profil Pošaljite privatnu poruku
dalmatinčica
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
Sarma = la pohva - posuda
6 = 10 - 4
PostPostano: 23:51 sub, 2. 6. 2012    Naslov: Citirajte i odgovorite
kako razviti f(x)=ln(x) oko c=0?
hvala
:?:
kako razviti f(x)=ln(x) oko c=0?
hvala
Question


[Vrh]
Korisnički profil Pošaljite privatnu poruku
quark
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: muško
Sarma = la pohva - posuda
20 = 26 - 6
PostPostano: 0:35 ned, 3. 6. 2012    Naslov: Citirajte i odgovorite
@humbert: nedostaje li ti limes? :lol:

Onda dobiješ da ti je limes 1 i D'Alembert ne može onda donijeti odluku.

@dalmatincica: imaš razvoj za ln(1+x); kako tebi treba ln(x) samo napiši ln(1+(x-1)) i gotovo :D
@humbert: nedostaje li ti limes? Laughing

Onda dobiješ da ti je limes 1 i D'Alembert ne može onda donijeti odluku.

@dalmatincica: imaš razvoj za ln(1+x); kako tebi treba ln(x) samo napiši ln(1+(x-1)) i gotovo Very Happy


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Zenon
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
PostPostano: 0:43 ned, 3. 6. 2012    Naslov: Citirajte i odgovorite
[quote="Hubert Cumberdale"][dtex] \frac{|a_{n+1}|}{|a_{n}|} = \frac{e^{-H_{n+1}}}{e^{-H_n}} = \frac{e^{-(H_{n}+\frac{1}{n+1})}}{e^{-H_n}}=\frac{{e^{-H_n}}*e^{-\frac{1}{n+1}}}{e^{-H_n}} = e^{-\frac{1}{n+1}} < 1 ,[/dtex] iz čega slijedi da je [tex]\Sigma a_n [/tex] apsolutno konvergentan red??
[/quote]

Kada n ide u beskonačnost [tex]-\frac{1}{n+1}[/tex] ide u 0, pa [tex]e^{-\frac{1}{n+1}}[/tex] ide u 1, a to nam ne govori ništa ( što vjerovatno znaš i sama ).
Inače kod primjene tog korolara koji slijedi iz D'Alembertovog kriterija ( pa tako i Cauchyjevog ) gledamo limese. Ako malo pogledaš same teoreme i dokaze vidjet ćeš da to što ti tvrdiš nije dovoljno.
U samim teoremima mi tražimo da postoji [tex]0\leq q< 1[/tex] takav da je taj razlomak ( odn. n-ti korijen ) nakon nekog mjesta uvijek manji od [tex]q[/tex], ali to u ovom slučaju jednostavno nije istina jer je funkcija rastuća i konvergira prema 1, pa za svaki epsilon veći od nule možemo naći [tex]n_0[/tex] takav da čim je [tex]n\geq n_0[/tex] da je beskonačno mnogo preostalih članova niza u epsilon okolini oko jedinice, što znači da ne možeš pronaći takav [tex]q[/tex] za ovaj niz.

I nemoj govoriti da si glupa. Kao prvo, to nije lijepo, kao drugo, i da jesi to ne moraju svi znati, a kao treće, čak i da jesi, tvoje nerazumjevanje zadatka je pokazatelj toga, isto kao što je konvergencija gore navedenog niza prema 1 pokazatelj konvergencije/divergencije reda :P
Hubert Cumberdale (napisa):
[dtex] \frac{|a_{n+1}|}{|a_{n}|} = \frac{e^{-H_{n+1}}}{e^{-H_n}} = \frac{e^{-(H_{n}+\frac{1}{n+1})}}{e^{-H_n}}=\frac{{e^{-H_n}}*e^{-\frac{1}{n+1}}}{e^{-H_n}} = e^{-\frac{1}{n+1}} < 1 ,[/dtex] iz čega slijedi da je [tex]\Sigma a_n [/tex] apsolutno konvergentan red??


Kada n ide u beskonačnost [tex]-\frac{1}{n+1}[/tex] ide u 0, pa [tex]e^{-\frac{1}{n+1}}[/tex] ide u 1, a to nam ne govori ništa ( što vjerovatno znaš i sama ).
Inače kod primjene tog korolara koji slijedi iz D'Alembertovog kriterija ( pa tako i Cauchyjevog ) gledamo limese. Ako malo pogledaš same teoreme i dokaze vidjet ćeš da to što ti tvrdiš nije dovoljno.
U samim teoremima mi tražimo da postoji [tex]0\leq q< 1[/tex] takav da je taj razlomak ( odn. n-ti korijen ) nakon nekog mjesta uvijek manji od [tex]q[/tex], ali to u ovom slučaju jednostavno nije istina jer je funkcija rastuća i konvergira prema 1, pa za svaki epsilon veći od nule možemo naći [tex]n_0[/tex] takav da čim je [tex]n\geq n_0[/tex] da je beskonačno mnogo preostalih članova niza u epsilon okolini oko jedinice, što znači da ne možeš pronaći takav [tex]q[/tex] za ovaj niz.

I nemoj govoriti da si glupa. Kao prvo, to nije lijepo, kao drugo, i da jesi to ne moraju svi znati, a kao treće, čak i da jesi, tvoje nerazumjevanje zadatka je pokazatelj toga, isto kao što je konvergencija gore navedenog niza prema 1 pokazatelj konvergencije/divergencije reda Razz



_________________
It's a wonderful, wonderful life!
[tex]\heartsuit \ \mathcal{PMF-MO} \ \heartsuit[/tex]
[tex]\mathbb Z\Sigma\mathbb N\emptyset\mathbb N[/tex]
[Vrh]
Korisnički profil Pošaljite privatnu poruku
shimija
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 22. 01. 2007. (18:33:54)
Postovi: (138)16
Spol: kućni ljubimac
Sarma = la pohva - posuda
53 = 55 - 2
Lokacija: Spljit
PostPostano: 12:37 ned, 3. 6. 2012    Naslov: Citirajte i odgovorite
[quote="dalmatinčica"]kako razviti f(x)=ln(x) oko c=0?
hvala
:?:[/quote]
Kad bi se to moglo, onda bi to značilo da je funckija [tex]\ln x[/tex] analitička pa time i klase [tex]C^\infty[/tex] oko nule. Međutim ona uopće nije definirana u nuli tako da je to očita kontradikcija.

quark je sugerirao razvoj oko točke [tex]c=1[/tex].
dalmatinčica (napisa):
kako razviti f(x)=ln(x) oko c=0?
hvala
Question

Kad bi se to moglo, onda bi to značilo da je funckija [tex]\ln x[/tex] analitička pa time i klase [tex]C^\infty[/tex] oko nule. Međutim ona uopće nije definirana u nuli tako da je to očita kontradikcija.

quark je sugerirao razvoj oko točke [tex]c=1[/tex].


[Vrh]
Korisnički profil Pošaljite privatnu poruku
PermutiranoPrase
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 10. 09. 2011. (16:08:19)
Postovi: (F4)16
Spol: kućni ljubimac
Sarma = la pohva - posuda
10 = 17 - 7
PostPostano: 13:49 ned, 3. 6. 2012    Naslov: Citirajte i odgovorite
Joj, hvala vam! Prosvijetljena sam na još jednom području. Moje šanse da preživim analizu rastu. :2pivce:
Nevezano, ali moram primjetiti - Hubert Cumberdale, do you like rusty spoons? :D
Joj, hvala vam! Prosvijetljena sam na još jednom području. Moje šanse da preživim analizu rastu. Neka zvone case!
Nevezano, ali moram primjetiti - Hubert Cumberdale, do you like rusty spoons? Very Happy



_________________
With great power comes great electricity bill.
n!!!!
Theorem 2: Alexander the Great did not exist and he had an infinite number of limbs.
[Vrh]
Korisnički profil Pošaljite privatnu poruku
malalodacha
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 11. 10. 2011. (17:06:13)
Postovi: (79)16
Sarma = la pohva - posuda
-24 = 9 - 33
PostPostano: 15:22 ned, 3. 6. 2012    Naslov: Citirajte i odgovorite
(x^2 /(16+x^4))^2 treba razviti u mclaurinov red. može pomoć oko toga, hitno?
(x^2 /(16+x^4))^2 treba razviti u mclaurinov red. može pomoć oko toga, hitno?


[Vrh]
Korisnički profil Pošaljite privatnu poruku
student_92
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 17. 09. 2011. (16:31:46)
Postovi: (B9)16
Sarma = la pohva - posuda
10 = 16 - 6
PostPostano: 15:41 ned, 3. 6. 2012    Naslov: Citirajte i odgovorite
[quote="malalodacha"](x^2 /(16+x^4))^2 treba razviti u mclaurinov red. može pomoć oko toga, hitno?[/quote]

Unaprijed se ispričavam na nekorištenju LaTex-a. Ovo sam radio na brzinu pa je možda negdje neka greška, ali idejno mi se čini ok.

Prvo si raspiši nazivnik tako da dobiješ 256 * (1+(x/2)^4)^2, zatim uvedi supstituciju t = x/2.
Trebaš dobiti izraz t^4 / (16*(1+t^4)^2), a potom izračunaj derivaciju funkcije (1/(1+t^4)) pa ćeš vidjeti što ćeš dobiti.
Preostaje ti deriviranje član po član i pažljivo vraćanje supstitucije.
malalodacha (napisa):
(x^2 /(16+x^4))^2 treba razviti u mclaurinov red. može pomoć oko toga, hitno?


Unaprijed se ispričavam na nekorištenju LaTex-a. Ovo sam radio na brzinu pa je možda negdje neka greška, ali idejno mi se čini ok.

Prvo si raspiši nazivnik tako da dobiješ 256 * (1+(x/2)^4)^2, zatim uvedi supstituciju t = x/2.
Trebaš dobiti izraz t^4 / (16*(1+t^4)^2), a potom izračunaj derivaciju funkcije (1/(1+t^4)) pa ćeš vidjeti što ćeš dobiti.
Preostaje ti deriviranje član po član i pažljivo vraćanje supstitucije.


[Vrh]
Korisnički profil Pošaljite privatnu poruku
malalodacha
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 11. 10. 2011. (17:06:13)
Postovi: (79)16
Sarma = la pohva - posuda
-24 = 9 - 33
PostPostano: 16:23 ned, 3. 6. 2012    Naslov: Citirajte i odgovorite
ajde napiši taj razvoj kako ispadne na kraju
ajde napiši taj razvoj kako ispadne na kraju


[Vrh]
Korisnički profil Pošaljite privatnu poruku
simon11
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (21:02:52)
Postovi: (7C)16
Spol: zombi
Sarma = la pohva - posuda
23 = 25 - 2
Lokacija: FunkyTown
PostPostano: 16:26 ned, 3. 6. 2012    Naslov: Citirajte i odgovorite
[quote="malalodacha"](x^2 /(16+x^4))^2 treba razviti u mclaurinov red. može pomoć oko toga, hitno?[/quote]

[latex]\frac{x^4}{(16+x^4)^2}=\frac{1}{16+x^4}-\frac{16}{(16+x^4)^2}[/latex]

[latex]\frac{1}{16+x^4}=\frac{1}{16(1+\frac{x^4}{16})}[/latex]

[latex]t=-\frac{x^4}{16}[/latex]

[latex]\frac{1}{16+x^4}=\frac{1}{16}\sum_{n=0}^{\infty}(-\frac{x^4}{16})^n=\sum_{n=0}^{\infty}\frac{(-1)^n}{16^{n+1}}x^{4n}[/latex]
sada deriviraj s lijeve strane se dobije

[latex]\frac{-4x^3}{(16+x^4)^2}[/latex] pomnozi s x i podijeli s -4 i dobije se pocetni izraz inace pogledaj si post od vjekovca on je skoro iNdentican :)

[quote="piccola"]Može pomoć? Treba ispitati konvergenciju redova:
2. [size=18][tex]\sum\frac{n!}{n^n}[/tex][/size][/quote]

ako se izracuna

[tex] \lim_{n \to \infty}{\frac{n!}{n^n}}=\infty[\tex]

dakle nije zadovoljen nuzan uvjet [latex]\rightarrow [\latex] divergira

[quote="piccola"]Može pomoć? Treba ispitati konvergenciju redova:

1. [size=18][tex]\sum\frac{cos(\frac{n\pi}{2})}{\sqrt{n}[/tex][/size][/quote]

nisam siguran ali mozda bi trebalo rastvaiti na tri slucaja jer cos moze biti samo 0,-1,1 pa bi se onda moglo rastaviti kao neki alternirajuci red npr

[latex]\frac{(-1)^n}{\sqrt(n)}[/latex] sto konvergira prema Leibnitzu,ali nisam siguran, a za apsolutnu konverg.stvarno neam ideje
malalodacha (napisa):
(x^2 /(16+x^4))^2 treba razviti u mclaurinov red. može pomoć oko toga, hitno?









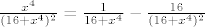
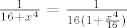
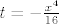
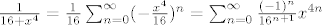
sada deriviraj s lijeve strane se dobije

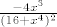pomnozi s x i podijeli s -4 i dobije se pocetni izraz inace pogledaj si post od vjekovca on je skoro iNdentican Smile

piccola (napisa):
Može pomoć? Treba ispitati konvergenciju redova:
2. [tex]\sum\frac{n!}{n^n}[/tex]


ako se izracuna

[tex] \lim_{n \to \infty}{\frac{n!}{n^n}}=\infty[\tex]

dakle nije zadovoljen nuzan uvjet sto konvergira prema Leibnitzu,ali nisam siguran, a za apsolutnu konverg.stvarno neam ideje



_________________
#Usa
getting recognized

Zadnja promjena: simon11; 16:40 ned, 3. 6. 2012; ukupno mijenjano 2 put/a.
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Zenon
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
PostPostano: 16:36 ned, 3. 6. 2012    Naslov: Citirajte i odgovorite
Ne valja ti to simon11:
D'Alembertov kriterij:
[dtex]\frac{\frac{(n+1)!}{(n+1)^{n+1}}}{\frac{n!}{n^n}}=\frac{(n+1)n^n}{(n+1)(n+1)^n}=\left(\frac{n}{n+1}\right)^n=\left[\left(1+\frac 1n\right)^n\right]^{-1}\to \frac{1}{e}[/dtex]
Ni u kojem slučaju ne može divergirati opći član u kad [tex]n^n[/tex] puno brže raste od [tex]n![/tex] .
Ne valja ti to simon11:
D'Alembertov kriterij:
[dtex]\frac{\frac{(n+1)!}{(n+1)^{n+1}}}{\frac{n!}{n^n}}=\frac{(n+1)n^n}{(n+1)(n+1)^n}=\left(\frac{n}{n+1}\right)^n=\left[\left(1+\frac 1n\right)^n\right]^{-1}\to \frac{1}{e}[/dtex]
Ni u kojem slučaju ne može divergirati opći član u kad [tex]n^n[/tex] puno brže raste od [tex]n![/tex] .



_________________
It's a wonderful, wonderful life!
[tex]\heartsuit \ \mathcal{PMF-MO} \ \heartsuit[/tex]
[tex]\mathbb Z\Sigma\mathbb N\emptyset\mathbb N[/tex]
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Prethodni postovi:   
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Matematička analiza 1 i 2 Vremenska zona: GMT + 01:00.
Idite na Prethodno  1, 2, 3, 4, 5, 6, 7  Sljedeće
Stranica 3 / 7.

 
Forum(o)Bir:  
Ne možete otvarati nove teme.
Ne možete odgovarati na postove.
Ne možete uređivati Vaše postove.
Ne možete izbrisati Vaše postove.
Ne možete glasovati u anketama.
You can attach files in this forum
You can download files in this forum


Powered by phpBB © 2001, 2002 phpBB Group
Theme created by Vjacheslav Trushkin
HR (Cro) by Ančica Sečan