| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
 Postano: 17:52 sub, 21. 8. 2004 Naslov: Re: Problem vezan uz sumu broja perm sa m fix tocaka Postano: 17:52 sub, 21. 8. 2004 Naslov: Re: Problem vezan uz sumu broja perm sa m fix tocaka |
    |
|
|
Nisi lud, stvarno vrijedi [latex]\sum_{m=0}^nD_n(m) = \sum_{m=0}^nmD_n(m)=n![/latex]. U drugoj sumi mozes preci na [i]m[/i]=1,...,[i]n[/i] (jer mnozis sa [i]m[/i]), pa neces imati problem sa [i]n[/i] povrh -1. Ja znam samo za generalizirane binomne koeficijente kod kojih je gore realan broj, a dolje mora biti prirodan broj ili nula.
Btw, kako bi se jednakost [latex]\sum_{m=0}^nmD_n(m)=n![/latex] interpretirala kombinatorno?
Nisi lud, stvarno vrijedi 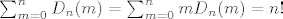 . U drugoj sumi mozes preci na m=1,...,n (jer mnozis sa m), pa neces imati problem sa n povrh -1. Ja znam samo za generalizirane binomne koeficijente kod kojih je gore realan broj, a dolje mora biti prirodan broj ili nula. . U drugoj sumi mozes preci na m=1,...,n (jer mnozis sa m), pa neces imati problem sa n povrh -1. Ja znam samo za generalizirane binomne koeficijente kod kojih je gore realan broj, a dolje mora biti prirodan broj ili nula.
Btw, kako bi se jednakost 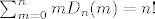 interpretirala kombinatorno? interpretirala kombinatorno?
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 9:53 ned, 22. 8. 2004 Naslov: Re: Problem vezan uz sumu broja perm sa m fix tocaka Postano: 9:53 ned, 22. 8. 2004 Naslov: Re: Problem vezan uz sumu broja perm sa m fix tocaka |
    |
|
|
[quote="krcko"]Nisi lud, stvarno vrijedi [latex]\sum_{m=0}^nD_n(m) = \sum_{m=0}^nmD_n(m)=n![/latex].[/quote]
:blueshock: A-Ha :g: al sad sam zbilja zabrinut :D jer malo mi je nepojmljivo da :noidea: ..........
[quote="krcko"]U drugoj sumi mozes preci na [i]m[/i]=1,...,[i]n[/i] (jer mnozis sa [i]m[/i]), pa neces imati problem sa [i]n[/i] povrh -1. Ja znam samo za generalizirane binomne koeficijente kod kojih je gore realan broj, a dolje mora biti prirodan broj ili nula.
Btw, kako bi se jednakost [latex]\sum_{m=0}^nmD_n(m)=n![/latex] interpretirala kombinatorno?[/quote]
.... da je suma niza nenegativnih cijelih brojeva jednaka sumi tog istog niza ako bi svaki clan niza mnozili sa razlicitim prirodnim brojevima :crazyeyes: (osim, naravno ako svi clanovi tog niza nisu jednaki nuli :D ali to cini se, nije slucaj jer im je suma n! :tso: )
| krcko (napisa): | Nisi lud, stvarno vrijedi 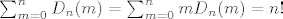 . . |
 A-Ha A-Ha  al sad sam zbilja zabrinut al sad sam zbilja zabrinut  jer malo mi je nepojmljivo da jer malo mi je nepojmljivo da  .......... ..........
| krcko (napisa): | U drugoj sumi mozes preci na m=1,...,n (jer mnozis sa m), pa neces imati problem sa n povrh -1. Ja znam samo za generalizirane binomne koeficijente kod kojih je gore realan broj, a dolje mora biti prirodan broj ili nula.
Btw, kako bi se jednakost 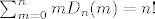 interpretirala kombinatorno? interpretirala kombinatorno? |
.... da je suma niza nenegativnih cijelih brojeva jednaka sumi tog istog niza ako bi svaki clan niza mnozili sa razlicitim prirodnim brojevima  (osim, naravno ako svi clanovi tog niza nisu jednaki nuli (osim, naravno ako svi clanovi tog niza nisu jednaki nuli  ali to cini se, nije slucaj jer im je suma n! ali to cini se, nije slucaj jer im je suma n!  ) )
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
|
| [Vrh] |
|
cinik
Forumaš(ica)


Pridružen/a: 27. 04. 2003. (23:34:09)
Postovi: (1FB)16
Spol: 
Lokacija: /proc/sys/cpu/
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
|
| [Vrh] |
|
cinik
Forumaš(ica)


Pridružen/a: 27. 04. 2003. (23:34:09)
Postovi: (1FB)16
Spol: 
Lokacija: /proc/sys/cpu/
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 2:17 sub, 28. 8. 2004 Naslov: Re: Problem vezan uz sumu broja perm sa m fix tocaka Postano: 2:17 sub, 28. 8. 2004 Naslov: Re: Problem vezan uz sumu broja perm sa m fix tocaka |
    |
|
|
[quote="cinik"]Hmmmm... Jedino sto mi pada na pamet jest igranje pokera ili bilo koje druge kartaske igre sa virtualnim (imaginarnim!) kartama, pa bi dakle 2+3i bilo nesto tipa imas 2 prave i 3 izmisljene karte u ruci i medju njima biras cetiri da ih zamijenis. To mozes uciniti na PUUUUUNO nacina, pogotovo ako dozvolis da imaginarne ne moraju biti iz standardnog spila.[/quote]
KHM ! :D ok, ako si ti offtopic, onda sam i ja, al... :rotfl: koliko to mora biti "nestandardan spil" :lol: da bi [latex]\displaystyle {2+3i\choose 4}[/latex] imao smisleno rijesenje :lol: ?
| cinik (napisa): | | Hmmmm... Jedino sto mi pada na pamet jest igranje pokera ili bilo koje druge kartaske igre sa virtualnim (imaginarnim!) kartama, pa bi dakle 2+3i bilo nesto tipa imas 2 prave i 3 izmisljene karte u ruci i medju njima biras cetiri da ih zamijenis. To mozes uciniti na PUUUUUNO nacina, pogotovo ako dozvolis da imaginarne ne moraju biti iz standardnog spila. |
KHM !  ok, ako si ti offtopic, onda sam i ja, al... ok, ako si ti offtopic, onda sam i ja, al...  koliko to mora biti "nestandardan spil" koliko to mora biti "nestandardan spil"  da bi da bi 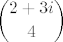 imao smisleno rijesenje imao smisleno rijesenje  ? ?
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
 Postano: 21:47 uto, 31. 8. 2004 Naslov: Re: Problem vezan uz sumu broja perm sa m fix tocaka Postano: 21:47 uto, 31. 8. 2004 Naslov: Re: Problem vezan uz sumu broja perm sa m fix tocaka |
    |
|
|
[quote="veky"]Mi smo u više navrata smatrali binomne koeficijente s negativnim (ipak, cjelobrojnim) "nazivnikom" jednakima nuli. Tako i :bow: Knuth radi... stvar se slaže sa svim interpretacijama binomnih koeficijenata koje mi sad padaju na pamet, i s većinom normalnih formulâ s njima.[/quote]
Sasvim slucajno nabasao na ovo...
[quote="Gian-Carlo Rota"]What is the "right" generalization of the binomial coefficients [latex]n \choose k[/latex] when k is allowed to be a negative integer? This question leads, in turn, to a third question: How shall we know whether a generalization of the binomial coefficients is "right"? The answer to this third question is easy: a generalization of the binomial coefficients is "right" if it leads to a sensible generalization of the binomial theorem:
[latex]\displaystyle (a+x)^n = \sum_{k=0}^n {n\choose k} a^kx^{n-k}.[/latex]
When I was young, I used to think of the binomial theorem as trivial. I think I have learned my lession. A well-known philosopher, I can't remember his name, wrote that the whole universe can be inferred from a grain of sand. He should have added that a great deal of mathematics can be derived by meditating upon the binomial theorem.
Let us take the bull by the horns and state the "right" generalization of the binomial coefficients. We proceed in the most pedestrian way, by first generalizing the definition of the factorial. Thus, let n be any integer, positive or negative. We define the Roman factorial [n]! as follows:
[latex]\displaystyle [n]!=n!$ if $n\ge 0;[/latex]
[latex]\displaystyle [n]!={(-1)^{n+1}\over (-n-1)!}$ if $n<0.[/latex]
From where does this definition come? I could simply say that it works, but that would not be the whole truth. The value of the Roman factorial [n]! for n negative equals the residue of the gamma function at the integer n-1. Using the Roman factorial, we define the Roman coefficients as follows:
[latex]\displaystyle \left[{n\atop k}\right] = {[n]! \over [k]![n-k]!}.[/latex]
When [latex]n\ge k \ge 0[/latex], the Roman coefficients coincide with the binomial coefficients. For all integers n and k, the Roman coefficients share all elementary properties of binomial coefficients, such as Pascal's triangle and so on. However, there are some surprises in store; for example, for k positive, we find
[latex]\displaystyle \left[{0 \atop -k}\right] = \left[{0 \atop k}\right] = {(-1)^{k+1}\over k}.[/latex]
Does this make any sense? Well, yes, because we can find a generalization of the binomial theorem that goes with this. It is the following.[/quote]
Koga zanima nek procita clanak jer mi se vise ne da prepisivati. Clanak ima podnaslov "Exercises in wishful thinking" :) i izasao je u Mathematical Intelligencer vol. 21, no. 2, 1999. Kao bonus u istom broju imate clanak o konacnim geometrijama "YEA WHY TRY HER RAW WET HAT" i filozofiranje realnim brojevima u kojem ih se usporedjuje sa "toaster fish" (bice s glavom u obliku tostera i tijelom ribe :silly: ). Trenutno je kod mene, uskoro cu vratiti pa mozete posuditi u knjiznici.
| veky (napisa): | Mi smo u više navrata smatrali binomne koeficijente s negativnim (ipak, cjelobrojnim) "nazivnikom" jednakima nuli. Tako i  Knuth radi... stvar se slaže sa svim interpretacijama binomnih koeficijenata koje mi sad padaju na pamet, i s većinom normalnih formulâ s njima. Knuth radi... stvar se slaže sa svim interpretacijama binomnih koeficijenata koje mi sad padaju na pamet, i s većinom normalnih formulâ s njima. |
Sasvim slucajno nabasao na ovo...
| Gian-Carlo Rota (napisa): | What is the "right" generalization of the binomial coefficients 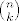 when k is allowed to be a negative integer? This question leads, in turn, to a third question: How shall we know whether a generalization of the binomial coefficients is "right"? The answer to this third question is easy: a generalization of the binomial coefficients is "right" if it leads to a sensible generalization of the binomial theorem: when k is allowed to be a negative integer? This question leads, in turn, to a third question: How shall we know whether a generalization of the binomial coefficients is "right"? The answer to this third question is easy: a generalization of the binomial coefficients is "right" if it leads to a sensible generalization of the binomial theorem:
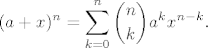
When I was young, I used to think of the binomial theorem as trivial. I think I have learned my lession. A well-known philosopher, I can't remember his name, wrote that the whole universe can be inferred from a grain of sand. He should have added that a great deal of mathematics can be derived by meditating upon the binomial theorem.
Let us take the bull by the horns and state the "right" generalization of the binomial coefficients. We proceed in the most pedestrian way, by first generalizing the definition of the factorial. Thus, let n be any integer, positive or negative. We define the Roman factorial [n]! as follows:
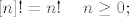
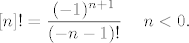
From where does this definition come? I could simply say that it works, but that would not be the whole truth. The value of the Roman factorial [n]! for n negative equals the residue of the gamma function at the integer n-1. Using the Roman factorial, we define the Roman coefficients as follows:
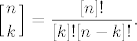
When 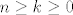 , the Roman coefficients coincide with the binomial coefficients. For all integers n and k, the Roman coefficients share all elementary properties of binomial coefficients, such as Pascal's triangle and so on. However, there are some surprises in store; for example, for k positive, we find , the Roman coefficients coincide with the binomial coefficients. For all integers n and k, the Roman coefficients share all elementary properties of binomial coefficients, such as Pascal's triangle and so on. However, there are some surprises in store; for example, for k positive, we find
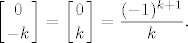
Does this make any sense? Well, yes, because we can find a generalization of the binomial theorem that goes with this. It is the following. |
Koga zanima nek procita clanak jer mi se vise ne da prepisivati. Clanak ima podnaslov "Exercises in wishful thinking"  i izasao je u Mathematical Intelligencer vol. 21, no. 2, 1999. Kao bonus u istom broju imate clanak o konacnim geometrijama "YEA WHY TRY HER RAW WET HAT" i filozofiranje realnim brojevima u kojem ih se usporedjuje sa "toaster fish" (bice s glavom u obliku tostera i tijelom ribe i izasao je u Mathematical Intelligencer vol. 21, no. 2, 1999. Kao bonus u istom broju imate clanak o konacnim geometrijama "YEA WHY TRY HER RAW WET HAT" i filozofiranje realnim brojevima u kojem ih se usporedjuje sa "toaster fish" (bice s glavom u obliku tostera i tijelom ribe  ). Trenutno je kod mene, uskoro cu vratiti pa mozete posuditi u knjiznici. ). Trenutno je kod mene, uskoro cu vratiti pa mozete posuditi u knjiznici.
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
|
|
| [Vrh] |
|
|






