| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
finalni
Forumaš(ica)


Pridružen/a: 04. 08. 2007. (11:48:53)
Postovi: (10D)16
Spol: 
Lokacija: Bloodbuzz Zagreb
|
|
| [Vrh] |
|
behemont
Forumaš(ica)

Pridružen/a: 12. 02. 2008. (21:21:19)
Postovi: (124)16
Spol: 
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
finalni
Forumaš(ica)


Pridružen/a: 04. 08. 2007. (11:48:53)
Postovi: (10D)16
Spol: 
Lokacija: Bloodbuzz Zagreb
|
|
| [Vrh] |
|
behemont
Forumaš(ica)

Pridružen/a: 12. 02. 2008. (21:21:19)
Postovi: (124)16
Spol: 
|
|
| [Vrh] |
|
finalni
Forumaš(ica)


Pridružen/a: 04. 08. 2007. (11:48:53)
Postovi: (10D)16
Spol: 
Lokacija: Bloodbuzz Zagreb
|
|
| [Vrh] |
|
behemont
Forumaš(ica)

Pridružen/a: 12. 02. 2008. (21:21:19)
Postovi: (124)16
Spol: 
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
 Postano: 23:28 ned, 20. 6. 2010 Naslov: Postano: 23:28 ned, 20. 6. 2010 Naslov: |
    |
|
|
De, odite na zeleni čaj umjesto da mi začetavate topik!
I još tu svašta nešto pišete o meni :rofl:
Sad me iti sram postavit pitanje.
Ma lažem.
Evo. Možda otkrivam toplu vodu, al` pokušajte razumjet da se prvi put susrećem s time, a žuri mi se, je l`.
Je l` nam aksiom dobre utemeljenosti zapravo govori da je prazan skup element svakog skupa?
Ako ne, šta nam onda on hoće poručit, a?
De, odite na zeleni čaj umjesto da mi začetavate topik!
I još tu svašta nešto pišete o meni 
Sad me iti sram postavit pitanje.
Ma lažem.
Evo. Možda otkrivam toplu vodu, al` pokušajte razumjet da se prvi put susrećem s time, a žuri mi se, je l`.
Je l` nam aksiom dobre utemeljenosti zapravo govori da je prazan skup element svakog skupa?
Ako ne, šta nam onda on hoće poručit, a?
_________________ mladac: e.k.s. je možda 8%, moje znanje ni toliko  |
|
| [Vrh] |
|
finalni
Forumaš(ica)


Pridružen/a: 04. 08. 2007. (11:48:53)
Postovi: (10D)16
Spol: 
Lokacija: Bloodbuzz Zagreb
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
kosani
Forumaš(ica)
Pridružen/a: 14. 11. 2010. (21:22:58)
Postovi: (26)16
|
 Postano: 15:37 čet, 3. 1. 2013 Naslov: Postano: 15:37 čet, 3. 1. 2013 Naslov: |
    |
|
|
Može pomoć oko dokaza Propozicije 2.25 (stranica 80)
Nije mi jasan ovaj dio kod trećeg pasosa od [i]Dokažimo sada da je B...[/i]
Uglavnom, uzeo sam primjer
[tex]A= \{1,3\}[/tex]
[tex]B = \bigcup_{(\alpha \in A)} \alpha = 1 \cup 3 = \cup \{1,3\} = \cup \{ \{0\}, \{0,1,2\} \} = \{0,1,2\} = 3[/tex]
Pošto očito za svaki [tex]\alpha \in A[/tex] vrijedi [tex] \alpha \subseteq B [/tex]
[tex] 1 \subseteq \{0,1,2\} [/tex] check
[tex] 3 \subseteq \{0,1,2\}[/tex] check tj. [tex] 3 = \{0,1,2\}[/tex]
te je B ordinalan broj, tada vrijedi [tex]\alpha \in \beta[/tex]
[tex]1 \in \{0,1,2\}[/tex] check
[tex]3 \in \{0,1,2\}[/tex] ?? Taj dio mi nije jasan.
Drugo pitanje, zašto pišemo oznaku [tex]B = \bigcup_{(\alpha \in A)}[/tex] , zašto ne možemo samo pisati [tex] B = \cup A [/tex] ?
Hvala
Može pomoć oko dokaza Propozicije 2.25 (stranica 80)
Nije mi jasan ovaj dio kod trećeg pasosa od Dokažimo sada da je B...
Uglavnom, uzeo sam primjer
[tex]A= \{1,3\}[/tex]
[tex]B = \bigcup_{(\alpha \in A)} \alpha = 1 \cup 3 = \cup \{1,3\} = \cup \{ \{0\}, \{0,1,2\} \} = \{0,1,2\} = 3[/tex]
Pošto očito za svaki [tex]\alpha \in A[/tex] vrijedi [tex] \alpha \subseteq B [/tex]
[tex] 1 \subseteq \{0,1,2\} [/tex] check
[tex] 3 \subseteq \{0,1,2\}[/tex] check tj. [tex] 3 = \{0,1,2\}[/tex]
te je B ordinalan broj, tada vrijedi [tex]\alpha \in \beta[/tex]
[tex]1 \in \{0,1,2\}[/tex] check
[tex]3 \in \{0,1,2\}[/tex] ?? Taj dio mi nije jasan.
Drugo pitanje, zašto pišemo oznaku [tex]B = \bigcup_{(\alpha \in A)}[/tex] , zašto ne možemo samo pisati [tex] B = \cup A [/tex] ?
Hvala
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
kosani
Forumaš(ica)
Pridružen/a: 14. 11. 2010. (21:22:58)
Postovi: (26)16
|
|
| [Vrh] |
|
zvonkec
Forumaš(ica)

Pridružen/a: 04. 11. 2010. (20:56:30)
Postovi: (37)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 20:11 sri, 9. 1. 2013 Naslov: Postano: 20:11 sri, 9. 1. 2013 Naslov: |
    |
|
|
[quote="zvonkec"]Meni na strani 70. u skripti piše sljedeća definicija (2.16) ordinalnih brojeva:
Za skup kažemo da je ordinlani broj ako je (x,biti element) DUS.
No u primjeru 2.17 pod b kaže da neki skupovi nisu ordinali jer nisu tranzitivni. Također, u korolaru 2.21 piše da je svaki skup ordinala DUS, a svaki tranzitivni skup ordinala je ordinal.Očito nešto nije u redu.Također se i u propoziciji 2.25 dokazuje da je B tranzitivan i DUS.
Moje pitanje je treba li u definiciji 2.16 skup x biti tranzitivan?[/quote]
Otvorio sam skriptu, meni definicija 2.16 glasi: Za skup x kažemo da je ordinalan broj ako je x tranzitivan skup i [latex](x, \in )[/latex] dobro uređen skup.
Tako da ne znam u kakvu ti skriptu gledaš, ali evo da otklonim sve moguće sumnje: tako je definirano i na predavanjima kod prof. Vukovića.
| zvonkec (napisa): | Meni na strani 70. u skripti piše sljedeća definicija (2.16) ordinalnih brojeva:
Za skup kažemo da je ordinlani broj ako je (x,biti element) DUS.
No u primjeru 2.17 pod b kaže da neki skupovi nisu ordinali jer nisu tranzitivni. Također, u korolaru 2.21 piše da je svaki skup ordinala DUS, a svaki tranzitivni skup ordinala je ordinal.Očito nešto nije u redu.Također se i u propoziciji 2.25 dokazuje da je B tranzitivan i DUS.
Moje pitanje je treba li u definiciji 2.16 skup x biti tranzitivan? |
Otvorio sam skriptu, meni definicija 2.16 glasi: Za skup x kažemo da je ordinalan broj ako je x tranzitivan skup i 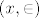 dobro uređen skup. dobro uređen skup.
Tako da ne znam u kakvu ti skriptu gledaš, ali evo da otklonim sve moguće sumnje: tako je definirano i na predavanjima kod prof. Vukovića.
|
|
| [Vrh] |
|
jabuka
Forumaš(ica)
Pridružen/a: 21. 11. 2009. (15:53:14)
Postovi: (7C)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
dodinho
Forumaš(ica)
Pridružen/a: 27. 09. 2011. (11:17:47)
Postovi: (4B)16
|
|
| [Vrh] |
|
@na
Forumaš(ica)

Pridružen/a: 16. 10. 2011. (13:29:26)
Postovi: (14)16
Spol: 
|
|
| [Vrh] |
|
|


















