| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
daric
Forumaš(ica)

Pridružen/a: 09. 12. 2010. (20:11:22)
Postovi: (D)16
|
|
| [Vrh] |
|
If and only if
Forumaš(ica)


Pridružen/a: 30. 09. 2012. (18:16:22)
Postovi: (1F)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 20:35 uto, 12. 2. 2013 Naslov: Postano: 20:35 uto, 12. 2. 2013 Naslov: |
    |
|
|
Zadatak nije dobro definiran.
1. Radimo li samo s cijelim brojevima? Izgleda mi kao da da, ali ovako napisano ne mogu biti siguran.
2. Sto znaci "pravokutnik što bliži kvadratu"?
Npr. za 50 imamo 5*10. Ocito, iz primjera, da ti to ne pase, ali moras reci sto je "sto blizi". Recimo da 7*7 nije tako blizu, bi li 6*8 bilo "dovoljno blizu kvadratu"?
Dakle, ima li neka gornja ograda na [tex]|a-b|[/tex] ili na neku vrstu relativne greske [tex]\frac{|a-b|}{a+b}[/tex] ili tako nesto?
@If and only if: Primjer ti steka kad je broj malo manji od potpunog kvadrata, npr. za 48 ces dobiti [tex](6-1)\cdot(6+1) = 35[/tex], umjesto (7-1)\cdot(7+1)=48[/tex].
Zadatak nije dobro definiran.
1. Radimo li samo s cijelim brojevima? Izgleda mi kao da da, ali ovako napisano ne mogu biti siguran.
2. Sto znaci "pravokutnik što bliži kvadratu"?
Npr. za 50 imamo 5*10. Ocito, iz primjera, da ti to ne pase, ali moras reci sto je "sto blizi". Recimo da 7*7 nije tako blizu, bi li 6*8 bilo "dovoljno blizu kvadratu"?
Dakle, ima li neka gornja ograda na [tex]|a-b|[/tex] ili na neku vrstu relativne greske [tex]\frac{|a-b|}{a+b}[/tex] ili tako nesto?
@If and only if: Primjer ti steka kad je broj malo manji od potpunog kvadrata, npr. za 48 ces dobiti [tex](6-1)\cdot(6+1) = 35[/tex], umjesto (7-1)\cdot(7+1)=48[/tex].
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
If and only if
Forumaš(ica)


Pridružen/a: 30. 09. 2012. (18:16:22)
Postovi: (1F)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 21:32 uto, 12. 2. 2013 Naslov: Postano: 21:32 uto, 12. 2. 2013 Naslov: |
    |
|
|
Ne. Recimo, za [tex]P := 272 = 16 \cdot 17[/tex], ti ces provjeriti [tex]\mathop{\rm round}(\sqrt{272}) = \mathop{\rm round}(16.4924225) = 16[/tex] i [tex](16-1)(16+1) = 15 \cdot 17 = 255[/tex]. Cak i da korijen zaokruzis na gore, dobit ces krivo: [tex](17-1)(17+1) = 16 \cdot 18 = 288[/tex].
Problem je sto ti trazis ili kvadrat ili pravokutnik kojem se duljine stranica razlikuju tocno za 2, sto funkcionira za direktne susjede potpunih kvadrata, ali ne i opcenito.
Rjesenje i dalje ovisi o definiciji koju gore trazim. Ograniciti se moze razmak izmedju stranica pravokutnika ili razlika povrsine pravokutnika i zadane povrsine ili neki treci parametar. Tek kad znamo sto je "pravokutnik što bliži kvadratu", mozemo razgovarati o algoritmu.
Osnovna ideja bi bila:
[code:1]x = najvece cijelo od sqrt(P)
dok (neki uvjet) {
y = zaokruzi(P / x);
provjeri odgovara li ti x*y vise od dosadasnjeg rjesenja; ako da, zapamti
}
ispisi/vrati nadjeni optimalni par (x,y)[/code:1]
Dakle, ne znamo uvjet petlje, no ne znamo niti sto znaci "odgovara vise". To moze biti nesto jednostavno, npr.
[tex]x,y \in \mathbb{N} \quad \text{takvi da je} \quad |P-xy| = \min\limits_{|a-b| \leq k} |P-ab| \quad \text{za neki zadani $k$}[/tex],
dakle pravokutnik s povrsinom najblizom zadanoj, a da mu se stranice razlikuju za manje od [tex]k[/tex], sto je los kriterij jer [tex]k[/tex] ne ovisi o redu velicine problema (tzv. apsolutna greska).
Nesto bolji uvjet bi bio da [tex]k[/tex] nekako ovisi o povrsini ili da se ogranici [b]omjer[/b] [tex]\frac{a}{b}[/tex] ili tako nesto (tzv. relativna greska).
No, moze se ubaciti i nekakva funkcija vrijednosti koja bi davala "vrijednost nekog rjesenja". Ugrubo, to bi znacilo da povrsina malo bliza trazenoj, ali uz bitno vecu razliku u duljinama stranica, znaci losije rjesenje od ponudjenog, dok znacajno priblizavanje toj povrsini uz manje povecanje razlike izmedju duljina stranica oznacava bolje rjesenje. Naravno, postavlja se pitanje tocne definicije funkcije vrijednosti.
Ne. Recimo, za [tex]P := 272 = 16 \cdot 17[/tex], ti ces provjeriti [tex]\mathop{\rm round}(\sqrt{272}) = \mathop{\rm round}(16.4924225) = 16[/tex] i [tex](16-1)(16+1) = 15 \cdot 17 = 255[/tex]. Cak i da korijen zaokruzis na gore, dobit ces krivo: [tex](17-1)(17+1) = 16 \cdot 18 = 288[/tex].
Problem je sto ti trazis ili kvadrat ili pravokutnik kojem se duljine stranica razlikuju tocno za 2, sto funkcionira za direktne susjede potpunih kvadrata, ali ne i opcenito.
Rjesenje i dalje ovisi o definiciji koju gore trazim. Ograniciti se moze razmak izmedju stranica pravokutnika ili razlika povrsine pravokutnika i zadane povrsine ili neki treci parametar. Tek kad znamo sto je "pravokutnik što bliži kvadratu", mozemo razgovarati o algoritmu.
Osnovna ideja bi bila:
| Kod: | x = najvece cijelo od sqrt(P)
dok (neki uvjet) {
y = zaokruzi(P / x);
provjeri odgovara li ti x*y vise od dosadasnjeg rjesenja; ako da, zapamti
}
ispisi/vrati nadjeni optimalni par (x,y) |
Dakle, ne znamo uvjet petlje, no ne znamo niti sto znaci "odgovara vise". To moze biti nesto jednostavno, npr.
[tex]x,y \in \mathbb{N} \quad \text{takvi da je} \quad |P-xy| = \min\limits_{|a-b| \leq k} |P-ab| \quad \text{za neki zadani $k$}[/tex],
dakle pravokutnik s povrsinom najblizom zadanoj, a da mu se stranice razlikuju za manje od [tex]k[/tex], sto je los kriterij jer [tex]k[/tex] ne ovisi o redu velicine problema (tzv. apsolutna greska).
Nesto bolji uvjet bi bio da [tex]k[/tex] nekako ovisi o povrsini ili da se ogranici omjer [tex]\frac{a}{b}[/tex] ili tako nesto (tzv. relativna greska).
No, moze se ubaciti i nekakva funkcija vrijednosti koja bi davala "vrijednost nekog rjesenja". Ugrubo, to bi znacilo da povrsina malo bliza trazenoj, ali uz bitno vecu razliku u duljinama stranica, znaci losije rjesenje od ponudjenog, dok znacajno priblizavanje toj povrsini uz manje povecanje razlike izmedju duljina stranica oznacava bolje rjesenje. Naravno, postavlja se pitanje tocne definicije funkcije vrijednosti.
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
daric
Forumaš(ica)

Pridružen/a: 09. 12. 2010. (20:11:22)
Postovi: (D)16
|
|
| [Vrh] |
|
If and only if
Forumaš(ica)


Pridružen/a: 30. 09. 2012. (18:16:22)
Postovi: (1F)16
Spol: 
|
|
| [Vrh] |
|
daric
Forumaš(ica)

Pridružen/a: 09. 12. 2010. (20:11:22)
Postovi: (D)16
|
|
| [Vrh] |
|
DsAg
Forumaš(ica)


Pridružen/a: 02. 10. 2005. (12:28:28)
Postovi: (17)16
Spol: 
|
 Postano: 1:25 čet, 14. 2. 2013 Naslov: Postano: 1:25 čet, 14. 2. 2013 Naslov: |
    |
|
|
Ak imas volje i vremena se s tim zezat, moze probat jos jedan pristup (uz napomenu da ces za rjesenja dobit realne a ne prirodne brojeve) - mozes radit optimizaciju u Matlabu preko funkcije fmincon. Po meni, imat ces dvije varijable 'a' i 'b' (stranice pravokutnika) koje idu od 0 do [latex]\sqrt{P}[/latex], funkciju [latex]P=a \cdot b[/latex] koju zelis maximizirat i funkciju [latex]c=\left |a-b \right |[/latex] koju zelis minimizirat. Nazalost, trenutno nemam nit Matlab nit vremena s tim se krampat pa ces morat sam vidjet kako to tocno izvest. Al ovo bi trebalo dat najbolje rezultate.
Za slucaj da bas zelis dobiti prirodne brojeve, trebalo bi biti dosta samo na finalnim rjesenjima primijeniti funkciju round.
Ak imas volje i vremena se s tim zezat, moze probat jos jedan pristup (uz napomenu da ces za rjesenja dobit realne a ne prirodne brojeve) - mozes radit optimizaciju u Matlabu preko funkcije fmincon. Po meni, imat ces dvije varijable 'a' i 'b' (stranice pravokutnika) koje idu od 0 do 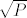 , funkciju , funkciju 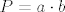 koju zelis maximizirat i funkciju koju zelis maximizirat i funkciju 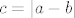 koju zelis minimizirat. Nazalost, trenutno nemam nit Matlab nit vremena s tim se krampat pa ces morat sam vidjet kako to tocno izvest. Al ovo bi trebalo dat najbolje rezultate. koju zelis minimizirat. Nazalost, trenutno nemam nit Matlab nit vremena s tim se krampat pa ces morat sam vidjet kako to tocno izvest. Al ovo bi trebalo dat najbolje rezultate.
Za slucaj da bas zelis dobiti prirodne brojeve, trebalo bi biti dosta samo na finalnim rjesenjima primijeniti funkciju round.
|
|
| [Vrh] |
|
|









