| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
uvelaruza
Forumaš(ica)
Pridružen/a: 05. 03. 2013. (13:30:02)
Postovi: (E)16
|
 Postano: 16:43 pet, 29. 3. 2013 Naslov: n-ti izvod Postano: 16:43 pet, 29. 3. 2013 Naslov: n-ti izvod |
    |
|
|
Moze li mi neko pomoci da resim zadatak?
Hvala unapred...
Moze li mi neko pomoci da resim zadatak?
Hvala unapred...
| Description: |
|

Download |
| Filename: |
zadatakk.pdf |
| Filesize: |
864.12 KB |
| Downloaded: |
335 Time(s) |
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 21:12 pet, 29. 3. 2013 Naslov: Postano: 21:12 pet, 29. 3. 2013 Naslov: |
    |
|
|
Nisam isao rjesavati. Ovo sto si ti predlozio se samo zakomplicira (barem ja ne vidim pravilo -- izvedi, recimo, prve 3 derivacije na Wolfram|Alpha). S druge strane, Taylor daje polinom koji u nuli ima tocno jedan clan (slobodni) koji ne ide nuzno u nulu. Ovdje se trazi [tex]n[/tex]-ta derivacija, hence moj prijedlog.
Nisam isao rjesavati. Ovo sto si ti predlozio se samo zakomplicira (barem ja ne vidim pravilo – izvedi, recimo, prve 3 derivacije na Wolfram|Alpha). S druge strane, Taylor daje polinom koji u nuli ima tocno jedan clan (slobodni) koji ne ide nuzno u nulu. Ovdje se trazi [tex]n[/tex]-ta derivacija, hence moj prijedlog.
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 21:47 pet, 29. 3. 2013 Naslov: Postano: 21:47 pet, 29. 3. 2013 Naslov: |
    |
|
|
[quote="Nightrider"]Ja ti opet govorim da ne znam je li ona ucila Taylorove redove.[/quote]
Jako lijepo da mi "opet govoris". Valjda sam preglup da iz prve shvatim. :roll: Pitao si kako bih dosao do izraza... pa sam ti raspisao zasto mi je Taylor pao na pamet. Ako odgovaram tebi, onda to nema veze s time je li netko tko vjerojatno nije niti s MO radio Taylora.
[quote="Nightrider"]Ali uocavas li ti da bi ti isao racunat Taylorov red od [latex]\ln f(x)[/latex] a ne od [latex]f(x)[/latex], i kad ga izracunas kako pronaci transformaciju koja red od [latex]\ln f(x)[/latex] transformira u red od [latex]f(x)[/latex], mozda da eksponenciras pa dobijes [latex]f(x)=e^{\ln f(x)}=e^{\sum_{i=0}^{\infty}\frac {f^{(n)}(c)(x-c)^n}{n!}}[/latex] pa onda imas e na red, i sto onda? Mozda sam ja jednostavno glup pa ne razumijem tvoje argumente, ajde budi malo jasniji?[/quote]
Sad cu ja tebi "opet govoriti": nisam rijesio. Rijec je o ideji koja moze i ne mora biti dobra. Uoci i da nam ne treba vise od prvih [tex]n[/tex] elemenata Taylora jer ce svi drugi nuzno iscezavati u nuli. To olaksava stvar; da li dovoljno ili se moze puno bolje/jednostavnije rijesiti, ne znam.
| Nightrider (napisa): | | Ja ti opet govorim da ne znam je li ona ucila Taylorove redove. |
Jako lijepo da mi "opet govoris". Valjda sam preglup da iz prve shvatim.  Pitao si kako bih dosao do izraza... pa sam ti raspisao zasto mi je Taylor pao na pamet. Ako odgovaram tebi, onda to nema veze s time je li netko tko vjerojatno nije niti s MO radio Taylora. Pitao si kako bih dosao do izraza... pa sam ti raspisao zasto mi je Taylor pao na pamet. Ako odgovaram tebi, onda to nema veze s time je li netko tko vjerojatno nije niti s MO radio Taylora.
| Nightrider (napisa): | Ali uocavas li ti da bi ti isao racunat Taylorov red od 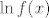 a ne od a ne od 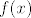 , i kad ga izracunas kako pronaci transformaciju koja red od , i kad ga izracunas kako pronaci transformaciju koja red od 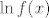 transformira u red od transformira u red od 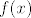 , mozda da eksponenciras pa dobijes , mozda da eksponenciras pa dobijes 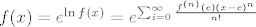 pa onda imas e na red, i sto onda? Mozda sam ja jednostavno glup pa ne razumijem tvoje argumente, ajde budi malo jasniji? pa onda imas e na red, i sto onda? Mozda sam ja jednostavno glup pa ne razumijem tvoje argumente, ajde budi malo jasniji? |
Sad cu ja tebi "opet govoriti": nisam rijesio. Rijec je o ideji koja moze i ne mora biti dobra. Uoci i da nam ne treba vise od prvih [tex]n[/tex] elemenata Taylora jer ce svi drugi nuzno iscezavati u nuli. To olaksava stvar; da li dovoljno ili se moze puno bolje/jednostavnije rijesiti, ne znam.
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
uvelaruza
Forumaš(ica)
Pridružen/a: 05. 03. 2013. (13:30:02)
Postovi: (E)16
|
 Postano: 23:48 pet, 29. 3. 2013 Naslov: Postano: 23:48 pet, 29. 3. 2013 Naslov: |
    |
|
|
Nismo ucili jos Tajlorov red... :( Pokusavala sam resiti sa pravilom logaritamskog deriviranja, ali nisam uspela, jer se suvise komplikuje, pa je tesko naci neko pravilo po kom bih nasla n-ti izvod (ili bar ja nisam tako uspela resiti).... Jos sam pokusavala preko Lajbnicovog pravila (nasla sam prvi izvod, pa posto je 1. izvod u vidu proizvoda, moze se primeniti Lajbnicova formula za n-ti izvod proizvoda dvije funkcije), i dobijem ja taj n-ti izvod, ali ni na osnovu cega ne mogu zakljuciti da je on deljiv sa n...
Hvala vam puno... Ja i dalje nisam dosla do resenja, pa ako se setite neke ideje, javite... Hvala jos jednom...
Nismo ucili jos Tajlorov red...  Pokusavala sam resiti sa pravilom logaritamskog deriviranja, ali nisam uspela, jer se suvise komplikuje, pa je tesko naci neko pravilo po kom bih nasla n-ti izvod (ili bar ja nisam tako uspela resiti).... Jos sam pokusavala preko Lajbnicovog pravila (nasla sam prvi izvod, pa posto je 1. izvod u vidu proizvoda, moze se primeniti Lajbnicova formula za n-ti izvod proizvoda dvije funkcije), i dobijem ja taj n-ti izvod, ali ni na osnovu cega ne mogu zakljuciti da je on deljiv sa n... Pokusavala sam resiti sa pravilom logaritamskog deriviranja, ali nisam uspela, jer se suvise komplikuje, pa je tesko naci neko pravilo po kom bih nasla n-ti izvod (ili bar ja nisam tako uspela resiti).... Jos sam pokusavala preko Lajbnicovog pravila (nasla sam prvi izvod, pa posto je 1. izvod u vidu proizvoda, moze se primeniti Lajbnicova formula za n-ti izvod proizvoda dvije funkcije), i dobijem ja taj n-ti izvod, ali ni na osnovu cega ne mogu zakljuciti da je on deljiv sa n...
Hvala vam puno... Ja i dalje nisam dosla do resenja, pa ako se setite neke ideje, javite... Hvala jos jednom...
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 0:39 sub, 30. 3. 2013 Naslov: Postano: 0:39 sub, 30. 3. 2013 Naslov: |
    |
|
|
Ako se sa g(x) oznaci [tex]g(x)=\frac{x}{1+x}+\ln(1+x)[/tex], onda je [tex]f'(x)=f(x)g(x)[/tex]. Po Leibnizovoj formuli imamo
[dtex]f^{(n)}(x)=(f(x)g(x))^{(n-1)}=\sum_{k=0}^{n-1}{n-1 \choose k}f^{(k)}(x)g^{(n-1-k)}(x).[/dtex]
Opca formula za n-tu derivaciju (n>0) od g se da naci.
[spoiler][tex]\displaystyle g^{(n)}(x)=(-1)^{n-1}(n-1)!\frac{n+(1+x)}{(1+x)^{n+1}}[/tex].[/spoiler]
[strike]Ostatak je indukcija[/strike] (greska uocena).
[spoiler]Pretpostavimo da tvrdnja vrijedi za svaki k<n. Nakon uvrstavanja u Leibnizovu formulu imamo:
[dtex]f^{(n)}(0)=\sum_{k=0}^{n-1}{n-1 \choose k}f^{(k)}(0)g^{(n-1-k)}(0)=\sum_{k=0}^{n-1}{n-1 \choose k}f^{(k)}(0)(-1)^{n-k-2}(n-k-2)!(n+1)=\sum_{k=0}^{n-1}(-1)^{n-k-2}\left[{n-1 \choose k}(n-k-2)!(n+1)\right]f^{(k)}(0).[/dtex]
Izraz u uglatim zagradama je nenegativan cijeli broj. Po pretpostavci indukcije k-te derivacije od f u nuli su djeljive s n pa je [tex]f^{(k)}(0)=kr_k[/tex], za neki cijeli broj [tex]r_k[/tex], gdje je [tex]0\leq k \leq n-1[/tex].
[strike]Nakon sredjivanja izraza, pojaviti ce se n! koji moze ici izvan sume.[/strike]
[/spoiler]
Edit: izgleda da je i ovaj pristup promasen; jako brzo se zakomplicira situacija sa sumama. Nakon koristenja Leibnizove formule i pretpostavke indukcije da je [tex]f^{(n-k)}(0)=(n-k)r_{n-k}[/tex], formulu za n-tu derivaciju sam sveo na [tex]f^{(n+1)}(0)=\sum_{k=1}^n(-1)^{k-1}(k-1)!(k+1)^2{n \choose k+1}r_{n-k}[/tex]. Vrlo je moguce da sam negdje pogrijesio.
Ako se sa g(x) oznaci [tex]g(x)=\frac{x}{1+x}+\ln(1+x)[/tex], onda je [tex]f'(x)=f(x)g(x)[/tex]. Po Leibnizovoj formuli imamo
[dtex]f^{(n)}(x)=(f(x)g(x))^{(n-1)}=\sum_{k=0}^{n-1}{n-1 \choose k}f^{(k)}(x)g^{(n-1-k)}(x).[/dtex]
Opca formula za n-tu derivaciju (n>0) od g se da naci.
| Spoiler [hidden; click to show]: | [tex]\displaystyle g^{(n)}(x)=(-1)^{n-1}(n-1)!\frac{n+(1+x)}{(1+x)^{n+1}}[/tex]. |
Ostatak je indukcija (greska uocena).
| Spoiler [hidden; click to show]: | Pretpostavimo da tvrdnja vrijedi za svaki k<n. Nakon uvrstavanja u Leibnizovu formulu imamo:
[dtex]f^{(n)}(0)=\sum_{k=0}^{n-1}{n-1 \choose k}f^{(k)}(0)g^{(n-1-k)}(0)=\sum_{k=0}^{n-1}{n-1 \choose k}f^{(k)}(0)(-1)^{n-k-2}(n-k-2)!(n+1)=\sum_{k=0}^{n-1}(-1)^{n-k-2}\left[{n-1 \choose k}(n-k-2)!(n+1)\right]f^{(k)}(0).[/dtex]
Izraz u uglatim zagradama je nenegativan cijeli broj. Po pretpostavci indukcije k-te derivacije od f u nuli su djeljive s n pa je [tex]f^{(k)}(0)=kr_k[/tex], za neki cijeli broj [tex]r_k[/tex], gdje je [tex]0\leq k \leq n-1[/tex].
Nakon sredjivanja izraza, pojaviti ce se n! koji moze ici izvan sume.
|
Edit: izgleda da je i ovaj pristup promasen; jako brzo se zakomplicira situacija sa sumama. Nakon koristenja Leibnizove formule i pretpostavke indukcije da je [tex]f^{(n-k)}(0)=(n-k)r_{n-k}[/tex], formulu za n-tu derivaciju sam sveo na [tex]f^{(n+1)}(0)=\sum_{k=1}^n(-1)^{k-1}(k-1)!(k+1)^2{n \choose k+1}r_{n-k}[/tex]. Vrlo je moguce da sam negdje pogrijesio.
_________________
The Dude Abides
Zadnja promjena: goranm; 15:49 sub, 30. 3. 2013; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 16:55 sub, 30. 3. 2013 Naslov: Postano: 16:55 sub, 30. 3. 2013 Naslov: |
    |
|
|
[quote="goranm"]
Edit: izgleda da je i ovaj pristup promasen; jako brzo se zakomplicira situacija sa sumama. Nakon koristenja Leibnizove formule i pretpostavke indukcije da je [tex]f^{(n-k)}(0)=(n-k)r_{n-k}[/tex], formulu za n-tu derivaciju sam sveo na [tex]f^{(n+1)}(0)=\sum_{k=1}^n(-1)^{k-1}(k-1)!(k+1)^2{n \choose k+1}r_{n-k}[/tex]. Vrlo je moguce da sam negdje pogrijesio.[/quote]
Ti si naisao na problem malo drugaciji od moga, meni se javlja clan kojeg nikako da izbjegnem a to je [tex](-1)!=\Gamma (0)=\infty[/tex], a tebi se javlja isto jedan problem samo nesto drugaciji. Nisam provjeravao ovaj tvoj izraz, no kako ti kazes, dobio si ovo, pa i neka je tocno izvedeno opet se javlja nesto gadno:
[tex]f^{(n+1)}(0)=\sum_{k=1}^n(-1)^{k-1}(k-1)!(k+1)^2{n \choose k+1}r_{n-k}[/tex] i zamisli da mi sad to idemo sumirat, dobijes da zadnji clan, za [tex]k=n[/tex] sadrzi binomni koeficijent [tex]{n \choose n+1}[/tex] a u binomnom koeficijentu gornji clan mora biti veci ili jednak donjemu (osim u generalizaciji binomnog koeficijenta na binomni red, ali ona nije ucila ni pojam reda a kamoli sto je to binomni red).
| goranm (napisa): |
Edit: izgleda da je i ovaj pristup promasen; jako brzo se zakomplicira situacija sa sumama. Nakon koristenja Leibnizove formule i pretpostavke indukcije da je [tex]f^{(n-k)}(0)=(n-k)r_{n-k}[/tex], formulu za n-tu derivaciju sam sveo na [tex]f^{(n+1)}(0)=\sum_{k=1}^n(-1)^{k-1}(k-1)!(k+1)^2{n \choose k+1}r_{n-k}[/tex]. Vrlo je moguce da sam negdje pogrijesio. |
Ti si naisao na problem malo drugaciji od moga, meni se javlja clan kojeg nikako da izbjegnem a to je [tex](-1)!=\Gamma (0)=\infty[/tex], a tebi se javlja isto jedan problem samo nesto drugaciji. Nisam provjeravao ovaj tvoj izraz, no kako ti kazes, dobio si ovo, pa i neka je tocno izvedeno opet se javlja nesto gadno:
[tex]f^{(n+1)}(0)=\sum_{k=1}^n(-1)^{k-1}(k-1)!(k+1)^2{n \choose k+1}r_{n-k}[/tex] i zamisli da mi sad to idemo sumirat, dobijes da zadnji clan, za [tex]k=n[/tex] sadrzi binomni koeficijent [tex]{n \choose n+1}[/tex] a u binomnom koeficijentu gornji clan mora biti veci ili jednak donjemu (osim u generalizaciji binomnog koeficijenta na binomni red, ali ona nije ucila ni pojam reda a kamoli sto je to binomni red).
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
uvelaruza
Forumaš(ica)
Pridružen/a: 05. 03. 2013. (13:30:02)
Postovi: (E)16
|
|
| [Vrh] |
|
|





















