| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 19:43 uto, 19. 3. 2013 Naslov: Diofantske jednadzbe Postano: 19:43 uto, 19. 3. 2013 Naslov: Diofantske jednadzbe |
    |
|
|
Neka je zadana diofantska jednadzba [latex]ax+by+cxy=d[/latex], pri cemu su [latex]{a,b,c\in\matbb Z} \setminus\{0\}[/latex], [latex]d\in\mathbb Z[/latex], traze se [latex]x,y\in\mathbb Z[/latex] koji zadovoljavaju jednadzbu.
1) Koje uvjete treba postavit na [latex]a,b,c,d[/latex] tako da jednadzba ima rjesenja?
2) Ako jednadzba ima barem jedno rjesenje da li tada ima beskonacno mnogo rjesenja (kao u slucaju [latex]c=0[/latex] )?
duje?
Neka je zadana diofantska jednadzba  , pri cemu su , pri cemu su 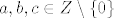 , , 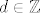 , traze se , traze se 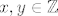 koji zadovoljavaju jednadzbu. koji zadovoljavaju jednadzbu.
1) Koje uvjete treba postavit na 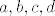 tako da jednadzba ima rjesenja? tako da jednadzba ima rjesenja?
2) Ako jednadzba ima barem jedno rjesenje da li tada ima beskonacno mnogo rjesenja (kao u slucaju  )? )?
duje?
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 20:46 uto, 19. 3. 2013 Naslov: Postano: 20:46 uto, 19. 3. 2013 Naslov: |
    |
|
|
Onda ste sad zapravo pokazali, da bez obzira kakvi bili uvjeti pod 1) da ovakva jednadzba ima uvijek konacno mnogo cjelobrojnih rjesenja, ili se to meni samo cini? :D
A ovo pod 1), imaju li neki jasni opci uvjeti na a,b,c,d koji garantiraju rjesenje (pritom ne mislim na nesto poput a+b+c=d pa imamo rjesenje (1,1))?
Da li bi upalilo nesto poput gcd(a,b,c)|d kao u slucaju linearne diofantske jednadzbe kada je c=0?
Onda ste sad zapravo pokazali, da bez obzira kakvi bili uvjeti pod 1) da ovakva jednadzba ima uvijek konacno mnogo cjelobrojnih rjesenja, ili se to meni samo cini? 
A ovo pod 1), imaju li neki jasni opci uvjeti na a,b,c,d koji garantiraju rjesenje (pritom ne mislim na nesto poput a+b+c=d pa imamo rjesenje (1,1))?
Da li bi upalilo nesto poput gcd(a,b,c)|d kao u slucaju linearne diofantske jednadzbe kada je c=0?
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 14:44 sri, 27. 3. 2013 Naslov: Postano: 14:44 sri, 27. 3. 2013 Naslov: |
    |
|
|
Rjesavajuci jedan problem sveo sam ga na problem nalazenja rjesenja diofantske jednadzbe koja je oblika na koji dosad nisam nikad naisao pa ako imate neki savjet kako pristupit problemu bio bih veoma zahvalan, a oblik jednadzbe slici obliku koji je postavljen u prvom pitanju samo sto se nekim cudom pojavila jos jedna varijabla ali s njom su (na svu srecu) dosla i dodatna ogranicenja na rjesenja, a problem glasi:
Da li diofantska jednadzba oblika: [dtex]axy+bx+cz=d[/dtex] ima samo konacno mnogo rjesenja, uz uvjet: [dtex]a,b,c,d\in\mathbb Z[/dtex] a uvjet na rjesenja je [dtex]x,y,z\in\mathbb N[/dtex] ?
Rjesavajuci jedan problem sveo sam ga na problem nalazenja rjesenja diofantske jednadzbe koja je oblika na koji dosad nisam nikad naisao pa ako imate neki savjet kako pristupit problemu bio bih veoma zahvalan, a oblik jednadzbe slici obliku koji je postavljen u prvom pitanju samo sto se nekim cudom pojavila jos jedna varijabla ali s njom su (na svu srecu) dosla i dodatna ogranicenja na rjesenja, a problem glasi:
Da li diofantska jednadzba oblika: [dtex]axy+bx+cz=d[/dtex] ima samo konacno mnogo rjesenja, uz uvjet: [dtex]a,b,c,d\in\mathbb Z[/dtex] a uvjet na rjesenja je [dtex]x,y,z\in\mathbb N[/dtex] ?
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 17:41 sri, 27. 3. 2013 Naslov: Postano: 17:41 sri, 27. 3. 2013 Naslov: |
    |
|
|
Sad sam malo bolje analizirao problem i uocio da nije rijec o 4 jednadzbe koje trebam proucit vec o 4 sustava jednadzbi, napisat cu vam kako sam pristupio problemu, necu napisat sva 4 sustava vec samo 1 jer su preostala 3 dosta slicna, znaci ovako:
Dobio sam sustav diofantskih jednadzbi: [dtex]12xy+x-3z=1[/dtex] [dtex]12xy+x-5w=16[/dtex] gdje su [dtex]x,y,z,w\in\mathbb N[/dtex].
Slijedece sto sam ucinio je da sam prvo taj sustav jednadzbi zbrojio pa sam ga iza oduzeo da dobijem ekvivalentan sustav: [dtex]24xy+2x-3z-5w=17[/dtex] [dtex]5w-3z=-15[/dtex].
Donja jednadzba je linearna diofantska jednazba i skup svih rjesenja je, kako sam dobio: [dtex]w=-30-3q[/dtex] [dtex]z=-45-5q[/dtex].
Sada sam te izraze ubacio u prvu jednadzbu (koju sam dobio zbrajanjem jednadzbi pocetnog sustava) i dobio jednadzbu koja je istog oblika kao one koje ste mi rjesavali u prethodnim pitanjima: [dtex]12xy+x+15q=-134[/dtex]
E sad ja nemam dobro istrenirano oko kao i vi da mogu s lakocom pronaci supstitucije koje daju skup rjesenja, ali ima jos jedan problem, jer su [dtex]z,w\in\mathbb N[/dtex] to implicira da treca varijabla sad nije prirodan broj: [dtex]q\in\mathbb Z , q<-10[/dtex].
Znaci trebam rijesiti slijedecu jednadzbu: [dtex]12xy+x+15q=-134[/dtex] sa uvjetima: [dtex]x,y\in\mathbb N , q\in\mathbb Z , q<-10[/dtex]
Pa ako me mozete pocastit sa nekim supstitucijama za ovu jednadzbu bio bih zahvalan. :D :D :D
Sad sam malo bolje analizirao problem i uocio da nije rijec o 4 jednadzbe koje trebam proucit vec o 4 sustava jednadzbi, napisat cu vam kako sam pristupio problemu, necu napisat sva 4 sustava vec samo 1 jer su preostala 3 dosta slicna, znaci ovako:
Dobio sam sustav diofantskih jednadzbi: [dtex]12xy+x-3z=1[/dtex] [dtex]12xy+x-5w=16[/dtex] gdje su [dtex]x,y,z,w\in\mathbb N[/dtex].
Slijedece sto sam ucinio je da sam prvo taj sustav jednadzbi zbrojio pa sam ga iza oduzeo da dobijem ekvivalentan sustav: [dtex]24xy+2x-3z-5w=17[/dtex] [dtex]5w-3z=-15[/dtex].
Donja jednadzba je linearna diofantska jednazba i skup svih rjesenja je, kako sam dobio: [dtex]w=-30-3q[/dtex] [dtex]z=-45-5q[/dtex].
Sada sam te izraze ubacio u prvu jednadzbu (koju sam dobio zbrajanjem jednadzbi pocetnog sustava) i dobio jednadzbu koja je istog oblika kao one koje ste mi rjesavali u prethodnim pitanjima: [dtex]12xy+x+15q=-134[/dtex]
E sad ja nemam dobro istrenirano oko kao i vi da mogu s lakocom pronaci supstitucije koje daju skup rjesenja, ali ima jos jedan problem, jer su [dtex]z,w\in\mathbb N[/dtex] to implicira da treca varijabla sad nije prirodan broj: [dtex]q\in\mathbb Z , q←10[/dtex].
Znaci trebam rijesiti slijedecu jednadzbu: [dtex]12xy+x+15q=-134[/dtex] sa uvjetima: [dtex]x,y\in\mathbb N , q\in\mathbb Z , q←10[/dtex]
Pa ako me mozete pocastit sa nekim supstitucijama za ovu jednadzbu bio bih zahvalan.   
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 18:09 sri, 27. 3. 2013 Naslov: Postano: 18:09 sri, 27. 3. 2013 Naslov: |
    |
|
|
Da li to otprilike znaci da ce jednadzba [dtex]axy+bx+cz=d[/dtex] uvijek imati beskonacan skup rjesenja ako ima jedno rjesenje, uz uvjet da uvjeti na a,b,c,d trivijalno ne iskljucuju rjesenja, poput a,b,c su parni a d neparan ili a,b,c su djeljivi sa m a d je prost itd...?
Da li to otprilike znaci da ce jednadzba [dtex]axy+bx+cz=d[/dtex] uvijek imati beskonacan skup rjesenja ako ima jedno rjesenje, uz uvjet da uvjeti na a,b,c,d trivijalno ne iskljucuju rjesenja, poput a,b,c su parni a d neparan ili a,b,c su djeljivi sa m a d je prost itd...?
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
 Postano: 18:55 sri, 27. 3. 2013 Naslov: Postano: 18:55 sri, 27. 3. 2013 Naslov: |
    |
|
|
Da, ako se rješenja traže u skupu cijelih brojeva.
Ako je (x0,y0,z0) jedno rješenje, onda je
x=x0+t*c, y=y0, z=z0-(a*y0+b)*t
takodjer rješenje za svaki cijeli broj t.
Ako se traže rješenja u prirodnim brojevima, onda će trebati još neki dodatni uvjet na prednake od a,b,c (tipa da su a i c različitih predznaka, ili nešto slično).
Da, ako se rješenja traže u skupu cijelih brojeva.
Ako je (x0,y0,z0) jedno rješenje, onda je
x=x0+t*c, y=y0, z=z0-(a*y0+b)*t
takodjer rješenje za svaki cijeli broj t.
Ako se traže rješenja u prirodnim brojevima, onda će trebati još neki dodatni uvjet na prednake od a,b,c (tipa da su a i c različitih predznaka, ili nešto slično).
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 15:22 ned, 7. 4. 2013 Naslov: Postano: 15:22 ned, 7. 4. 2013 Naslov: |
    |
|
|
Na jednom forumu nasa sam da jedan korisnik tvrdi da diofantska jednadzba [latex]{n\choose 2}=2{m\choose 2}[/latex] ima beskonacno mnogo rjesenja u prirodnim brojevima. I sad, meni to izgleda nevjerojatno, pa sam pokusao opovrgnuti tu tvrdnju, i to sam napravio na slijedeci nacin (ono sto me zanima je da li je nacin zakljucivanja na koji sam to napravio valjan, meni izgleda valjan), i ide sad:
Znaci imamo [latex]{n\choose 2}=2{m\choose 2}[/latex] sto je ekvivalentno sa [latex]P(n,m)=n^2-n-2(m^2-m)=0[/latex]. Amo to promatrat kao kvadratnu jednadzbu po varijabli n (pretvaram se da je [latex]2(m^2-m)[/latex] konstanta), rjesavanjem te kvadratne jednadzbe dobije se rjesenje za n: [latex]n={\frac {1\pm \sqrt {8m^2-8m+1}}{2}}[/latex]. E sad to ima smisla jedino ako je izraz pod korijenom kvadrat nekog prirodnog broja pa pisem [latex]8m^2-8m+1=k^2[/latex] pa, naravno, to promatram kao kvadratnu jednadzbu po varijabli m i dobijem rjesenje za m: [latex]m={\frac {8\pm \sqrt {64-4(1-k^2)}}{16}}[/latex]. To opet ima smisla samo ako je izraz pod korijenom kvadrat nekog prirodnog broja pa pisem: [latex]64-4(1-k^2)=l^2[/latex] sta je ekvivalentno sa [latex]l^2-4k^2=60[/latex] a to sa [latex](l-2k)(l+2k)=60[/latex] pa pocetna jednazba [latex]P(n,m)=0[/latex] nemoze imat beskonacno mnogo rjesenja jer bi to znacilo da broj 60 ima beskonacno mnogo faktora.
Je li ovo valjan pristup problemu?
Na jednom forumu nasa sam da jedan korisnik tvrdi da diofantska jednadzba 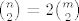 ima beskonacno mnogo rjesenja u prirodnim brojevima. I sad, meni to izgleda nevjerojatno, pa sam pokusao opovrgnuti tu tvrdnju, i to sam napravio na slijedeci nacin (ono sto me zanima je da li je nacin zakljucivanja na koji sam to napravio valjan, meni izgleda valjan), i ide sad: ima beskonacno mnogo rjesenja u prirodnim brojevima. I sad, meni to izgleda nevjerojatno, pa sam pokusao opovrgnuti tu tvrdnju, i to sam napravio na slijedeci nacin (ono sto me zanima je da li je nacin zakljucivanja na koji sam to napravio valjan, meni izgleda valjan), i ide sad:
Znaci imamo 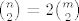 sto je ekvivalentno sa sto je ekvivalentno sa 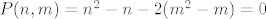 . Amo to promatrat kao kvadratnu jednadzbu po varijabli n (pretvaram se da je . Amo to promatrat kao kvadratnu jednadzbu po varijabli n (pretvaram se da je 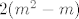 konstanta), rjesavanjem te kvadratne jednadzbe dobije se rjesenje za n: konstanta), rjesavanjem te kvadratne jednadzbe dobije se rjesenje za n: 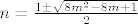 . E sad to ima smisla jedino ako je izraz pod korijenom kvadrat nekog prirodnog broja pa pisem . E sad to ima smisla jedino ako je izraz pod korijenom kvadrat nekog prirodnog broja pa pisem 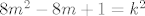 pa, naravno, to promatram kao kvadratnu jednadzbu po varijabli m i dobijem rjesenje za m: pa, naravno, to promatram kao kvadratnu jednadzbu po varijabli m i dobijem rjesenje za m: 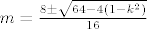 . To opet ima smisla samo ako je izraz pod korijenom kvadrat nekog prirodnog broja pa pisem: . To opet ima smisla samo ako je izraz pod korijenom kvadrat nekog prirodnog broja pa pisem:  sta je ekvivalentno sa sta je ekvivalentno sa 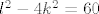 a to sa a to sa 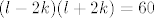 pa pocetna jednazba pa pocetna jednazba 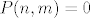 nemoze imat beskonacno mnogo rjesenja jer bi to znacilo da broj 60 ima beskonacno mnogo faktora. nemoze imat beskonacno mnogo rjesenja jer bi to znacilo da broj 60 ima beskonacno mnogo faktora.
Je li ovo valjan pristup problemu?
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
|























